Dado un número N , la tarea es encontrar el número de pares (a, b) en el rango [1, N] tal que su MCM no sea igual a su producto, es decir, MCM(a, b) != (a* b) y (b > a) . Puede haber múltiples consultas para responder.
Ejemplos:
Entrada: Q[] = {5}
Salida: 1
Explicación:
El par del 1 al 5 es (2, 4)
Entrada: Q[] = {5, 7}
Salida: 1, 4
Explicación:
El par del 1 al 5 es (2, 4)
Los pares del 1 al 7 son (2, 4), (2, 6), (3, 6), (4, 6)
Planteamiento: La idea es utilizar la Función Totient de Euler .
1. Encuentra el número total de pares que se pueden formar usando números del 1 al N. El número de pares formados es igual a ( N * (N – 1)) / 2 .
2. Para cada entero i ≤ N, utilice la función Totient de Euler para encontrar todos los pares coprimos con i y almacenarlos en la array.
Ejemplo:
arr[10] = 10 * (1-1/2) * (1-1/5)
= 4
3.
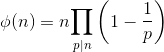
4. Ahora construya la tabla de suma de prefijos que almacena la suma de todos los phi(i) para todos los i entre 1 y N. Usando esto, podemos responder cada consulta en O(1) tiempo.
5. Finalmente, la respuesta para cualquier i ≤ N viene dada por la diferencia entre el número total de pares formados y pref[i].
A continuación se muestra la implementación del enfoque dado:
C++
// C++ program to find the count of pairs
// from 1 to N such that their LCM
// is not equal to their product
#include <bits/stdc++.h>
using namespace std;
#define N 100005
// To store Euler's Totient Function
int phi[N];
// To store prefix sum table
int pref[N];
// Compute Totients of all numbers
// smaller than or equal to N
void precompute()
{
// Make phi[1]=0 since 1 cannot form any pair
phi[1] = 0;
// Initialise all remaining phi[] with i
for (int i = 2; i < N; i++)
phi[i] = i;
// Compute remaining phi
for (int p = 2; p < N; p++) {
// If phi[p] is not computed already,
// then number p is prime
if (phi[p] == p) {
// phi of prime number is p-1
phi[p] = p - 1;
// Update phi of all multiples of p
for (int i = 2 * p; i < N; i += p) {
// Add the contribution of p
// to its multiple i by multiplying
// it with (1 - 1/p)
phi[i] = (phi[i] / p) * (p - 1);
}
}
}
}
// Function to store prefix sum table
void prefix()
{
// Prefix Sum of all Euler's Totient Values
for (int i = 1; i < N; i++)
pref[i] = pref[i - 1] + phi[i];
}
void find_pairs(int n)
{
// Total number of pairs that can be formed
int total = (n * (n - 1)) / 2;
int ans = total - pref[n];
cout << "Number of pairs from 1 to "
<< n << " are " << ans << endl;
}
// Driver Code
int main()
{
// Function call to compute all phi
precompute();
// Function call to store all prefix sum
prefix();
int q[] = { 5, 7 };
int n = sizeof(q) / sizeof(q[0]);
for (int i = 0; i < n; i++) {
find_pairs(q[i]);
}
return 0;
}
Java
// Java program to find the count of pairs
// from 1 to N such that their LCM
// is not equal to their product
class GFG{
static final int N = 100005;
// To store Euler's Totient Function
static int []phi = new int[N];
// To store prefix sum table
static int []pref = new int[N];
// Compute Totients of all numbers
// smaller than or equal to N
static void precompute()
{
// Make phi[1] = 0 since 1 cannot form any pair
phi[1] = 0;
// Initialise all remaining phi[] with i
for (int i = 2; i < N; i++)
phi[i] = i;
// Compute remaining phi
for (int p = 2; p < N; p++) {
// If phi[p] is not computed already,
// then number p is prime
if (phi[p] == p) {
// phi of prime number is p-1
phi[p] = p - 1;
// Update phi of all multiples of p
for (int i = 2 * p; i < N; i += p) {
// Add the contribution of p
// to its multiple i by multiplying
// it with (1 - 1/p)
phi[i] = (phi[i] / p) * (p - 1);
}
}
}
}
// Function to store prefix sum table
static void prefix()
{
// Prefix Sum of all Euler's Totient Values
for (int i = 1; i < N; i++)
pref[i] = pref[i - 1] + phi[i];
}
static void find_pairs(int n)
{
// Total number of pairs that can be formed
int total = (n * (n - 1)) / 2;
int ans = total - pref[n];
System.out.print("Number of pairs from 1 to "
+ n + " are " + ans +"\n");
}
// Driver Code
public static void main(String[] args)
{
// Function call to compute all phi
precompute();
// Function call to store all prefix sum
prefix();
int q[] = { 5, 7 };
int n = q.length;
for (int i = 0; i < n; i++) {
find_pairs(q[i]);
}
}
}
// This code contributed by Rajput-Ji
Python3
# Python 3 program to find the count of pairs
# from 1 to N such that their LCM
# is not equal to their product
N = 100005
# To store Euler's Totient Function
phi = [0 for i in range(N)]
# To store prefix sum table
pref = [0 for i in range(N)]
# Compute Totients of all numbers
# smaller than or equal to N
def precompute():
# Make phi[1]=0 since 1 cannot form any pair
phi[1] = 0
# Initialise all remaining phi[] with i
for i in range(2, N, 1):
phi[i] = i
# Compute remaining phi
for p in range(2,N):
# If phi[p] is not computed already,
# then number p is prime
if (phi[p] == p):
# phi of prime number is p-1
phi[p] = p - 1
# Update phi of all multiples of p
for i in range(2*p, N, p):
# Add the contribution of p
# to its multiple i by multiplying
# it with (1 - 1/p)
phi[i] = (phi[i] // p) * (p - 1)
# Function to store prefix sum table
def prefix():
# Prefix Sum of all Euler's Totient Values
for i in range(1, N, 1):
pref[i] = pref[i - 1] + phi[i]
def find_pairs(n):
# Total number of pairs that can be formed
total = (n * (n - 1)) // 2
ans = total - pref[n]
print("Number of pairs from 1 to",n,"are",ans)
# Driver Code
if __name__ == '__main__':
# Function call to compute all phi
precompute()
# Function call to store all prefix sum
prefix()
q = [5, 7]
n = len(q)
for i in range(n):
find_pairs(q[i])
# This code is contributed by Surendra_Gangwar
C#
// C# program to find the count of pairs
// from 1 to N such that their LCM
// is not equal to their product
using System;
class GFG{
static readonly int N = 100005;
// To store Euler's Totient Function
static int []phi = new int[N];
// To store prefix sum table
static int []pref = new int[N];
// Compute Totients of all numbers
// smaller than or equal to N
static void precompute()
{
// Make phi[1] = 0 since 1
// cannot form any pair
phi[1] = 0;
// Initialise all remaining
// phi[] with i
for(int i = 2; i < N; i++)
phi[i] = i;
// Compute remaining phi
for(int p = 2; p < N; p++)
{
// If phi[p] is not computed already,
// then number p is prime
if (phi[p] == p)
{
// phi of prime number is p-1
phi[p] = p - 1;
// Update phi of all multiples of p
for(int i = 2 * p; i < N; i += p)
{
// Add the contribution of p
// to its multiple i by multiplying
// it with (1 - 1/p)
phi[i] = (phi[i] / p) * (p - 1);
}
}
}
}
// Function to store prefix sum table
static void prefix()
{
// Prefix Sum of all
// Euler's Totient Values
for(int i = 1; i < N; i++)
pref[i] = pref[i - 1] + phi[i];
}
static void find_pairs(int n)
{
// Total number of pairs
// that can be formed
int total = (n * (n - 1)) / 2;
int ans = total - pref[n];
Console.Write("Number of pairs from 1 to " +
n + " are " + ans + "\n");
}
// Driver Code
public static void Main(String[] args)
{
// Function call to compute all phi
precompute();
// Function call to store
// all prefix sum
prefix();
int []q = {5, 7};
int n = q.Length;
for(int i = 0; i < n; i++)
{
find_pairs(q[i]);
}
}
}
// This code is contributed by Rajput-Ji
Javascript
<script>
// javascript program to find the count of pairs
// from 1 to N such that their LCM
// is not equal to their product
var N = 100005;
// To store Euler's Totient Function
var phi = Array(N).fill(0);
// To store prefix sum table
var pref = Array(N).fill(0);
// Compute Totients of all numbers
// smaller than or equal to N
function precompute() {
// Make phi[1] = 0 since 1 cannot form any pair
phi[1] = 0;
// Initialise all remaining phi with i
for (i = 2; i < N; i++)
phi[i] = i;
// Compute remaining phi
for (p = 2; p < N; p++) {
// If phi[p] is not computed already,
// then number p is prime
if (phi[p] == p) {
// phi of prime number is p-1
phi[p] = p - 1;
// Update phi of all multiples of p
for (i = 2 * p; i < N; i += p) {
// Add the contribution of p
// to its multiple i by multiplying
// it with (1 - 1/p)
phi[i] = (phi[i] / p) * (p - 1);
}
}
}
}
// Function to store prefix sum table
function prefix() {
// Prefix Sum of all Euler's Totient Values
for (i = 1; i < N; i++)
pref[i] = pref[i - 1] + phi[i];
}
function find_pairs(n) {
// Total number of pairs that can be formed
var total = (n * (n - 1)) / 2;
var ans = total - pref[n];
document.write("Number of pairs from 1 to " + n + " are " + ans + "<br/>");
}
// Driver Code
// Function call to compute all phi
precompute();
// Function call to store all prefix sum
prefix();
var q = [ 5, 7 ];
var n = q.length;
for (i = 0; i < n; i++) {
find_pairs(q[i]);
}
// This code contributed by Rajput-Ji
</script>
Number of pairs from 1 to 5 are 1 Number of pairs from 1 to 7 are 4
Complejidad temporal: O(n 2 )
Espacio Auxiliar: O(n)
Publicación traducida automáticamente
Artículo escrito por cherry0697 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA