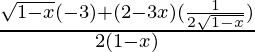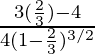Clase 12 Soluciones RD Sharma – Capítulo 18 Máximos y Mínimos – Ejercicio 18.2

Posted on by Rudeus Greyrat

Encuentre los puntos de máximos locales o mínimos locales, si los hay, de las siguientes funciones, usando la prueba de la primera derivada. Además, encuentre los valores máximos locales o mínimos locales, según sea el caso:

Pregunta 1. f(x) = (x – 5) 4

Solución:

función dada 

f(x) = (x – 5) 4

Ahora, diferencie la función dada wrt x

f'(x) = 4(x-5) 3

Ahora, para máximos y mínimos locales  

Pon f'(x) = 0

⇒ 4(x – 5) 3 = 0

⇒ x – 5 = 0

⇒ x = 5

Entonces, en x = 5, f'(x) cambia de negativo a positivo. Por lo tanto, x = 5 es el punto de mínimos locales 

Entonces, el valor mínimo es f(5) = (5 – 5) 4 = 0

Pregunta 2. f(x) = x 3 – 3x

Solución:

función dada 

f(x) = x3 – 3x

Ahora, diferencie la función dada wrt x

f'(x) = 3x 2 – 3

Ahora, para máximos y mínimos locales  

Pon f'(x) = 0

⇒ 3x 2 – 3 = 0

⇒x = ±1

Ahora, diferenciando de nuevo la función f'(x) con x

f “(x) = 6x

Pon x = 1 en f”(x)

f “(1)= 6 > 0

Entonces, x = 1 es el punto de mínimos locales  

Pon x = -1 en f”(x)

f “(-1)= -6 < 0

Entonces, x = -1 es el punto de los máximos locales  

Entonces, el valor mínimo es f(1) = x 3 – 3x = 1 3 – 3 = -2

y el valor máximo es f(-1) = x 3 – 3x = (-1) 3 – 3(-1) = 2                                  

Pregunta 3. f(x) = x 3 (x – 1) 2

Solución:

función dada 

f(x) = x 3 (x – 1) 2

Ahora, diferencie la función dada wrt x

f'(x) = 3x 2 (x- 1) 2 + 2x 3 (x- 1)

= (x – 1) (3x 2 (x – 1) + 2x 3 )  

= (x – 1) (3x 3 – 3x 2 + 2x 3 )

= (x – 1) (5x 3 – 3x 2 )

= x 2 (x – 1) (5x – 3)

Ahora, para todos los máximos y mínimos,

Pon f'(x) = 0

= x 2 (x – 1) (5x- 3) = 0

x = 0, 1, 3/5

Entonces, en x = 3/5, f'(x) cambia de negativo a positivo. Por lo tanto, x = 3/5 es un punto de mínimos

Entonces, el valor mínimo es f(3/5) = (3/5) 3 (3/5 – 1) 2 = 108/3125

En x = 1, f'(x) cambia de positivo a negativo. Por lo tanto, x = 1 es el punto de máximos.

Entonces, el valor máximo es f(1) = (1) 3 (1 – 1) 2 = 0

Pregunta 4. f (x) = (x – 1) (x + 2) 2

Solución:

función dada 

f(x) = (x – 1)(x + 2) 2

Ahora, diferencie la función dada wrt x

f'(x) = (x + 2) 2 + 2(x – 1)(x + 2)

= (x+ 2) (x+ 2 + 2x – 2)

 =(x + 2) (3x)

Ahora, para todos los máximos y mínimos,

Pon f'(x) = 0

⇒ (x + 2) (3x) = 0

x = 0,-2

Entonces, en x = -2, f(x) cambia de positivo a negativo. Por lo tanto, x = -2 es un punto de Maxima

Entonces, el valor máximo es f(-2) = (-2 – 1)(-2 + 2) 2 = 0

En x = 0, f ‘(x) cambia de negativo a positivo. Por lo tanto, x = 0 es el punto de mínimos.

Entonces, el valor mínimo es f(0) = (0 – 1)(0 + 2) 2 = -4

Pregunta 5. f(x) = (x – 1) 3 (x + 1) 2

Solución:

función dada 

f(x) = (x – 1) 3 (x + 1) 2

Ahora, diferencie la función dada wrt x

f'(x) = 3(x – 1) 2 (x + 1) 2 + 2(x – 1) 3 (x + 1)

= (x – 1) 2 (x + 1) {3 (x + 1) + 2 (x – 1)}

= (x – 1) 2 (x + 1) (5x + 1)

Ahora, para máximos y mínimos locales,

Pon f'(x) = 0

⇒ (x – 1) 2 (x + 1) (5x + 1) = 0

⇒ x = 1, -1, -1/5

Entonces, en x = -1, f ‘(x) cambia de positivo a negativo. Por lo tanto, x = -1 es el punto de máximos

Entonces, el valor máximo es f(-1) = (-1 – 1) 3 (-1 + 1) 2 = 0

En x = -1/5, f ‘(x) cambia de negativo a positivo, por lo que x= -1/5 es el punto de mínimos

Entonces, el valor mínimo es f(-1/5) = (-1/5 – 1) 3 (-1/5 + 1) 2 = -3456/3125

Pregunta 6. f(x) = x 3 – 6x 2 + 9x +15

Solución:

función dada 

f(x) = x3 – 6×2 + 9x + 15

Ahora, diferencie la función dada wrt x

f'(x) = 3x 2 – 12x + 9

= 3 (x 2 – 4x + 3)

= 3 (x-3) (x-1)

Ahora, para máximos y mínimos locales,

 Pon f'(x) = 0

⇒ 3 (x – 3) (x – 1) – 0

⇒ x = 3, 1

En x = 1, f'(x) cambia de positivo a negativo. Por lo tanto, x = 1 es el punto de los máximos locales

Entonces, el valor máximo es f(1) = (1) 3 – 6(1) 2 + 9(1) + 15 = 19

En x = 3, f'(x) cambia de negativo a positivo. Por lo tanto, x = 3 es el punto de mínimos locales

Entonces, el valor mínimo es f(x) = (3) 3 – 6(3) 2 + 9(3) + 15 = 15

Pregunta 7. f(x) = sen2x, 0 < x < π

Solución:

función dada 

f(x) = sen2x, 0 < x, π

Ahora, diferencie la función dada wrt x

f'(x) = 2 cos 2x

Ahora, para máximos y mínimos locales,

Pon f'(x) = 0

⇒ 2x = \frac{π}{2},\frac{3π}{2}

⇒ x = \frac{π}{4},\frac{3π}{4}

En x = , f'(x) cambia de positivo a negativo. Por lo tanto, x = , es el punto de los máximos locales

Entonces, el valor máximo es f() = sin2() = 1

En x = 3, f'(x) cambia de negativo a positivo. Por lo tanto, x = 3 es el punto de los mínimos locales,

Entonces, el valor mínimo es f(3) = sin2(3) = -1

Pregunta 8. f(x) = sen x – cos x, 0 < x < 2π

Solución:

función dada 

f(x) = sen x – cos x, 0 < x < 2π

Ahora, diferencie la función dada wrt x

f'(x)= cos x + sen x

Ahora, para máximos y mínimos locales,

Pon f'(x) =0 

cos x = -sen x 

tan x = -1

x =  \frac{3π}{4},\frac{7π}{4} ∈ (0, 2π)

Ahora de nuevo diferencie la función dada wrt x

f”(x) = -sen x + cos x

f"(\frac{3π}{4})=-sin\frac{3π}{4}+cos\frac{3π}{4}=-\frac{1}{√2}-\frac{1}{√2}=-√2 <0

f"(\frac{7π}{4})=-sin\frac{7π}{4}+cos\frac{7π}{4}=\frac{1}{√2}+\frac{1}{√2}=√2 >0

Por lo tanto, por el criterio de la segunda derivada,  x=\frac{3π}{4} es un punto de máximos locales 

Por lo tanto, el valor máximo es f(\frac{3π}{4})=sin\frac{3π}{4}-cos\frac{3π}{4}=\frac{1}{√2}+\frac{1}{√2}=√2.

Sin embargo,  x=\frac{7π}{4} es un punto de mínimos locales 

Por lo tanto, el valor mínimo es f(\frac{7π}{4})=sin\frac{7π}{4}-cos\frac{7π}{4}=-\frac{1}{√2}-\frac{1}{√2}=-√2

Pregunta 9. f(x) = cos x, 0< x < π

Solución:

función dada 

f(x) = cos x, 0< x < π

Ahora, diferencie la función dada wrt x

f'(x) = – sen x

Ahora, para máximos y mínimos locales,

 Pon f'(x) – 0

⇒ – sen x = 0

⇒ x = 0, y π

Pero, estos dos puntos se encuentran fuera del intervalo (0, π)

Entonces, no existirán máximos ni mínimos locales en el intervalo (0, π).

Pregunta 10. f(x) = sen 2x – x, -π/2 ≤ x ≤ π/2

Solución:

función dada 

f(x) = sen2x – x

Ahora, diferencie la función dada wrt x

f'(x) = 2 cos 2x – 1

Ahora, para máximos y mínimos locales,

Pon f'(x) = 0

⇒ 2cos 2x – 1 = 0

⇒ cos 2x = 1/2 = cos π/3

⇒ 2x = π/3, -π/3

⇒ x = \frac{π}{6},-\frac{π}{6}

En x = -π/6, f'(x) cambia de negativo a positivo. Por lo tanto, x = π/6 es el punto de mínimos locales.

Entonces, el valor mínimo es f(-\frac{π}{6})=\frac{-√3}{2}+\frac{π}{6}

En x = π/6, f'(x) cambia de positivo a negativo. Por lo tanto, x = π/6 es el punto de los máximos locales

El valor máximo es f(\frac{π}{6})=\frac{√3}{2}-\frac{π}{6}

Pregunta 11. f(x) = 2sen x – x, -π/2 ≤ x ≤ π/2

Solución:

función dada 

f(x) = 2sen x – x, -π/2≤ x ≤ π/2

Ahora, diferencie la función dada wrt x

f'(x) = 2cos x – 1 = 0

Ahora, para máximos y mínimos locales,

Pon f'(x) = 0

⇒ cos x = 1/2 = cos π/3

⇒ x = -π/3, π/3

Entonces, en x = -π/3, f'(x) cambia de negativo a positivo. Por lo tanto, x = -π/3 es el punto de mínimos locales 

Entonces, el valor mínimo es f(-π/3) = 2sin(-π/3) – (-π/3) = -√3 – π/3

En x = π/3, f'(x) cambia de positivo a negativo. Por lo tanto, x = π/3 es el punto de mínimos locales 

El valor máximo es f(π/3) = 2sin(π/3) – (π/3) = √3 – π/3

Pregunta 12. f(x) = x 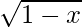\sqrt{1- x} , x > 0

Solución:

función dada 

f(x) = x \sqrt{1- x} , x > 0

Ahora, diferencie la función dada wrt x

f'(x) = \sqrt{1- x}+ x.\frac{1}{\sqrt{1- x}}(-1)=\sqrt{1- x}-\frac{x}{2\sqrt{1- x}}

= \frac{2(1-x)-x}{2\sqrt{1- x}}=\frac{2-3x}{2\sqrt{1- x}}

Ahora, para máximos y mínimos locales,

Pon f'(x) = 0

⇒ \frac{2-3x}{2\sqrt{1-x}}=0

⇒ 2 – 3x = 0

⇒ x = 2/3

f “(x) = \frac{1}{2}[\frac{\sqrt{1-x}(-3)-(2-3x)(\frac{-1}{2\sqrt{1-x}})}{1-x}]

=\frac{\sqrt{1-x}(-3)+(2-3x)(\frac{1}{2\sqrt{1-x}})}{2(1-x)}

= \frac{-6(1-x)+(2-3x)}{4(1-x)^{3/2}}

= (3x – 4)/4(1 – x) 2

f “(2/3) = \frac{3(\frac{2}{3})-4}{4(1-\frac{2}{3})^{3/2}}

= \frac{2-4}{4(\frac{1}{3})^{3/2}}

= \frac{-1}{2(\frac{1}{3})^{3/2}}<0

Por lo tanto, x = 2/3 es un punto de máximos locales y el valor máximo local de f en x = 2/3 es 

f(2/3) = 2/3(√1/3) = (2√3)/9

Pregunta 13. f(x) = x 3 (2x – 1) 3

Solución:

función dada 

f(x) = x3 ( 2x – 1) 3

Ahora, diferencie la función dada wrt x

f'(x) = 3x 2 (2x – 1) 2 + 6x 3 (2x – 1) 2

= 3x 2 (2x – 1) 2 (2x – 1 + 2x)

= 3x 2 (4x – 1) 

Ahora, para máximos y mínimos locales,

Pon f'(x) = 0

⇒ 3x 2 (4x – 1) = 0

⇒ x = 0, 1/4

En x = 1/4, f'(x) cambia de negativo a positivo. Por lo tanto, x = 1/4 es el punto de mínimos locales,

Entonces, el valor mínimo es f(1/4)= (1/4) 3 (2(1/4) – 1) 3 = -1/512

Pregunta 14. f(x) = x/2 + 2/x, x > 0

Solución:

función dada 

f(x) = x/2 + 2/x, x > 0

Ahora, diferencie la función dada wrt x

f'(x) = 1/2 – 2/x 2 , x > 0

Ahora, para máximos y mínimos locales,

Pon f'(x) = 0

⇒ 1/2 – 2/x2 = 0

⇒ x 2 – 4 = 0

⇒ x = 2, -2

En x = 2, f'(x) cambia de negativo a positivo. Por lo tanto, x = 2 es el punto de mínimos locales 

Entonces, el valor mínimo local es f(2) = 2/2 + 2/2 = 2

Pregunta 15. f(x) = 1/(x 2 + 2)

Solución:

función dada 

f(x) = 1/(x2 + 2 )

Ahora, diferencie la función dada wrt x

f'(x) = -(2x)/(x 2 + 2) 2

Ahora, para máximos y mínimos locales,

Ponga f'(x) = 0 f'(x) = 0 

f'(x) = -(2x)/(x 2 + 2) 2 = 0

⇒ x = 0

En x = 0 – , f'(x) > 0

En x = 0 + , f'(x) < 0

Por lo tanto, el valor mínimo y máximo local de f(0) = 1/2

Publicación traducida automáticamente

Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *