Compensación espacio-tiempo en algoritmos

En este artículo, discutiremos la compensación espacio-tiempo en los algoritmos. Una compensación es una situación en la que una cosa aumenta y otra disminuye. Es una forma de resolver un problema en:

• Ya sea en menos tiempo y utilizando más espacio, o
• En muy poco espacio pasando mucho tiempo.

El mejor algoritmo es el que ayuda a resolver un problema que requiere menos espacio en la memoria y también toma menos tiempo para generar la salida. Pero, en general, no siempre es posible lograr ambas condiciones al mismo tiempo. La condición más común es un algoritmo que utiliza una tabla de búsqueda . Esto significa que se pueden escribir las respuestas a algunas preguntas para cada valor posible. Una forma de resolver este problema es anotar toda la tabla de búsqueda , lo que le permitirá encontrar las respuestas muy rápidamente pero ocupará mucho espacio. Otra forma es calcular las respuestas sin escribir nada, lo que ocupa muy poco espacio, pero puede llevar mucho tiempo. Por lo tanto, cuantos más algoritmos eficientes en el tiempo tengas, serán menos eficientes en el espacio.

Tipos de intercambio de espacio-tiempo

• Datos comprimidos o sin comprimir
• Volver a renderizar o almacenar imágenes
• Código más pequeño o desenrollado de bucle
• Tablas de consulta o Recálculo

Datos comprimidos o sin comprimir :se puede aplicar una compensación de espacio-tiempo al problema delalmacenamiento de datos. Si los datos almacenados no están comprimidos, ocupa más espacio pero menos tiempo. Pero si los datos se almacenan comprimidos, se necesita menos espacio pero más tiempo para ejecutar el algoritmo de descompresión. Hay muchos casos en los que es posible trabajar directamente con datos comprimidos. En ese caso de índices bitmap comprimidos, donde es más rápido trabajar con compresión que sin compresión.

Volver a renderizar o imágenes almacenadas : en este caso, almacenar solo la fuente y renderizarla como una imagen tomaría más espacio pero menos tiempo, es decir, almacenar una imagen en el caché es más rápido que volver a renderizar pero requiere más espacio en la memoria.

Código más pequeño o desenrollado de bucle : el código más pequeño ocupa menos espacio en la memoria, pero requiere un tiempo de cálculo alto para volver al principio del bucle al final de cada iteración. El desenrollado de bucles puede optimizar la velocidad de ejecución a costa de aumentar el tamaño binario. Ocupa más espacio en la memoria pero requiere menos tiempo de cálculo.

Tablas de búsqueda o recálculo : en una tabla de búsqueda, una implementación puede incluir la tabla completa, lo que reduce el tiempo de cálculo pero aumenta la cantidad de memoria necesaria. Puede volver a calcular, es decir, computar las entradas de la tabla según sea necesario, lo que aumenta el tiempo de cálculo pero reduce los requisitos de memoria.

Por Ejemplo: En términos matemáticos, la secuencia F _n de los Números de Fibonacci está definida por la relación de recurrencia:

F _n = F _{n – 1} + F _{n – 2} , 
donde, F ₀ = 0 y F ₁ = 1.

Una solución simple para encontrar el N ^-ésimo término de Fibonacci usando la recursión de la relación de recurrencia anterior.

A continuación se muestra la implementación usando recursividad:

// C++ program to find Nth Fibonacci
// number using recursion
#include <iostream>
using namespace std;
 
// Function to find Nth Fibonacci term
int Fibonacci(int N)
{
    // Base Case
    if (N < 2)
        return N;
 
    // Recursively computing the term
    // using recurrence relation
    return Fibonacci(N - 1) + Fibonacci(N - 2);
}
 
// Driver Code
int main()
{
    int N = 5;
 
    // Function Call
    cout << Fibonacci(N);
 
    return 0;
}

// Java program to find Nth Fibonacci
// number using recursion
class GFG {
 
    // Function to find Nth Fibonacci term
    static int Fibonacci(int N)
    {
        // Base Case
        if (N < 2)
            return N;
 
        // Recursively computing the term
        // using recurrence relation
        return Fibonacci(N - 1) + Fibonacci(N - 2);
    }
 
    // Driver Code
    public static void main(String[] args)
    {
        int N = 5;
 
        // Function Call
        System.out.print(Fibonacci(N));
    }
}
 
// This code is contributed by rutvik_56.

// C# program to find Nth Fibonacci
// number using recursion
using System;
class GFG
{
 
  // Function to find Nth Fibonacci term
  static int Fibonacci(int N)
  {
 
    // Base Case
    if (N < 2)
      return N;
 
    // Recursively computing the term
    // using recurrence relation
    return Fibonacci(N - 1) + Fibonacci(N - 2);
  }
 
  // Driver Code
  public static void Main(string[] args)
  {
    int N = 5;
 
    // Function Call
    Console.Write(Fibonacci(N));
  }
}
 
// This code is contributed by pratham76.

# Python3 program to find Nth Fibonacci
# number using recursion
 
 
# Function to find Nth Fibonacci term
def Fibonacci(N:int):
    # Base Case
    if (N < 2):
        return N
 
    # Recursively computing the term
    # using recurrence relation
    return Fibonacci(N - 1) + Fibonacci(N - 2)
 
 
# Driver Code
if __name__ == '__main__':
    N = 5
 
    # Function Call
    print(Fibonacci(N))

5

Complejidad temporal: O(2 ^N )
Espacio auxiliar: O(1)

Explicación: La complejidad temporal de la implementación anterior es exponencial debido a los múltiples cálculos de los mismos subproblemas una y otra vez. El espacio auxiliar utilizado es mínimo. Pero nuestro objetivo es reducir la complejidad del tiempo del enfoque, incluso si requiere espacio adicional. A continuación se describe el enfoque optimizado.

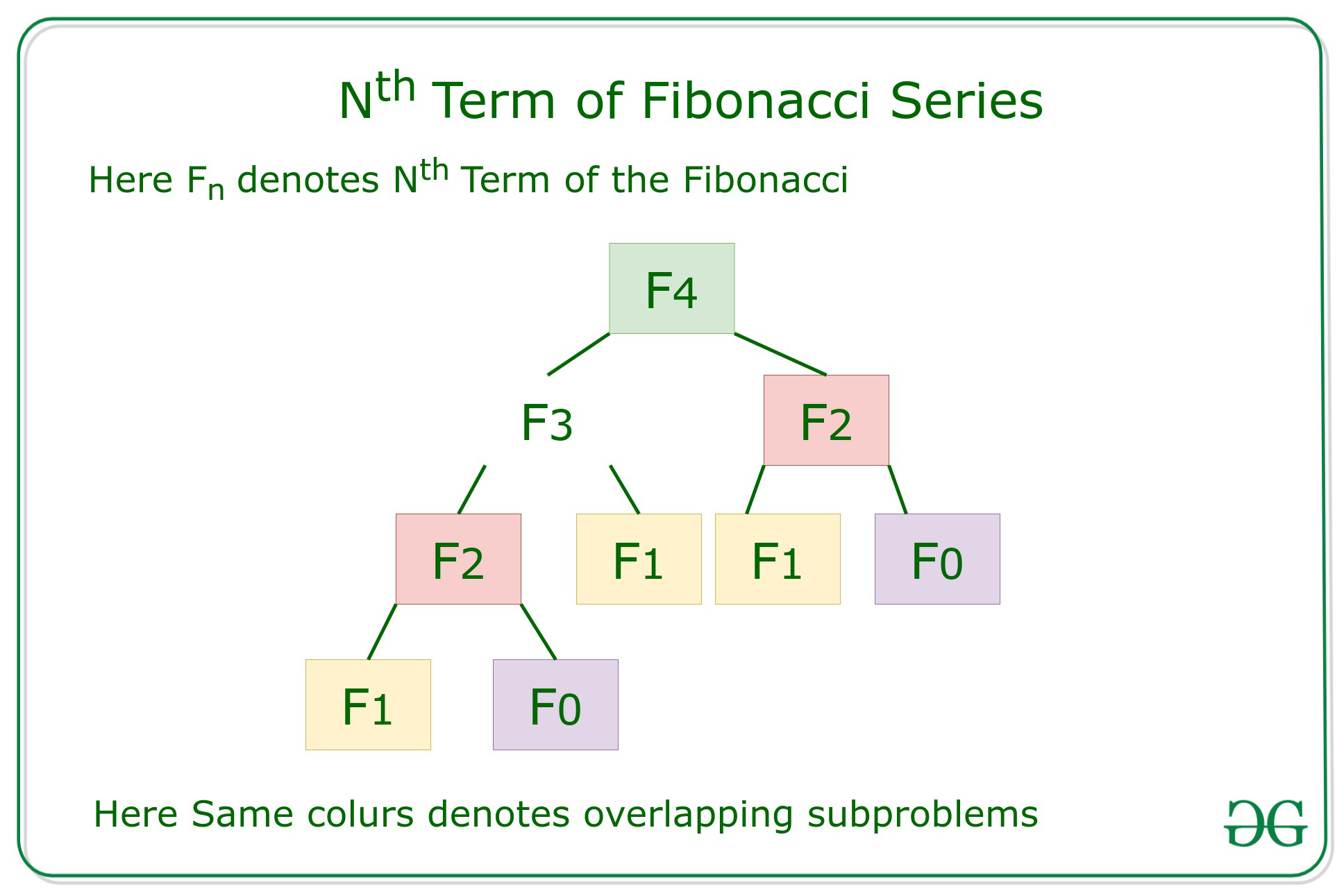
Enfoque eficiente: para optimizar el enfoque anterior, la idea es utilizar la programación dinámica para reducir la complejidad mediante la memorización de los subproblemas superpuestos , como se muestra en el siguiente árbol de recursión:

A continuación se muestra la implementación del enfoque anterior:

// C++ program to find Nth Fibonacci
// number using recursion
#include <iostream>
using namespace std;
 
// Function to find Nth Fibonacci term
int Fibonacci(int N)
{
    int f[N + 2];
    int i;
 
    // 0th and 1st number of the
    // series are 0 and 1
    f[0] = 0;
    f[1] = 1;
 
    // Iterate over the range [2, N]
    for (i = 2; i <= N; i++) {
 
        // Add the previous 2 numbers
        // in the series and store it
        f[i] = f[i - 1] + f[i - 2];
    }
 
    // Return Nth Fibonacci Number
    return f[N];
}
 
// Driver Code
int main()
{
    int N = 5;
 
    // Function Call
    cout << Fibonacci(N);
 
    return 0;
}

# Python3 program to find Nth Fibonacci
# number using recursion
 
# Function to find Nth Fibonacci term
def Fibonacci(N):
    f=[0]*(N + 2)
 
    # 0th and 1st number of the
    # series are 0 and 1
    f[0] = 0
    f[1] = 1
 
    # Iterate over the range [2, N]
    for i in range(2,N+1) :
 
        # Add the previous 2 numbers
        # in the series and store it
        f[i] = f[i - 1] + f[i - 2]
     
 
    # Return Nth Fibonacci Number
    return f[N]
 
 
# Driver Code
if __name__ == '__main__':
    N = 5
 
    # Function Call
    print(Fibonacci(N))

5

Complejidad temporal: O(N)
Espacio auxiliar: O(N)

Explicación: La complejidad de tiempo de la implementación anterior es lineal mediante el uso de un espacio auxiliar para almacenar los estados de los subproblemas superpuestos para que pueda usarse más cuando sea necesario.