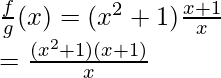Álgebra de funciones reales

Se puede pensar en una función como una regla o un conjunto de reglas que asignan una entrada a una salida conocida como su imagen. 

x ⇢ Función ⇢ y

Las letras como f, g o h se usan a menudo para describir una función. A veces, mientras se trabaja en problemas complejos, se requiere combinar dos o más funciones. Supongamos que tenemos una función que calcula cubos de los números dados como entrada, pero queremos que la salida siempre sea un número positivo. En este caso, es posible que deba combinar una función de cubo con una función absoluta. Estas combinaciones se emplean a menudo en la vida real, pero no siempre se pueden hacer tan fácilmente como en este caso. Necesitamos cuidar las cosas para que las combinaciones no den resultados indefinidos. Veamos las reglas o el álgebra de las funciones que nos ayudan a combinarlas. 

Álgebra de funciones reales

Adición de funciones

Sean f:X → R y g:X → R dos funciones reales cualesquiera, donde X ∈ R . Entonces definimos (f + g):X → R por 

(f + g) (x) = f (x) + g (x), para todo x ∈ X

Sean D(f) y D(g) el dominio de la función “f” y “g” respectivamente. El dominio en el caso de la suma de funciones se convierte en. 

D(f + g) = D(f) D(g)

Pregunta: Dado f(x) = x + 3 y g(x) = 2x. Encuentra (f + g)(x). 

Solución:

(f + g) (x) = f (x) + g (x). Dado que f(x) = x + 3 y g(x) = 2x. 

(f + g)(x) = x + 3 + 2x = 3x + 3

Dado que el dominio de ambas funciones es el número real R. La intersección del dominio también es R. Entonces, el dominio de (f + g)(x) es R. 

Resta de funciones

Sean f:X → R y g:X → R dos funciones reales cualesquiera, donde X ∈ R . Entonces definimos (f – g):X → R por

(f – g) (x) = f (x) – g (x), para todo x ∈ X

Sean D(f) y D(g) el dominio de la función “f” y “g” respectivamente. El dominio en el caso de la suma de funciones se convierte en.

D(f + g) = D(f) D(g)

Pregunta: Dado f(x) = x ² + 1 y g(x) = 1/x. Encuentre (fg)(x). 

Solución:

El dominio de f(x) es R pero el dominio de g(x) es R – {0}.  

(f – g)(x) = f(x) – g(x) = x ² + 1 – 1/x. Pero el dominio para (f – g)(x) es RR – {0} = R – {0}. 

Multiplicación por un escalar

Sea f: X → R una función real y “ k ” cualquier escalar perteneciente a R. Entonces el producto kf es una función de X a R definida por 

(kf)(x) = kf(x), x ∈ X .

El dominio sigue siendo el mismo en este caso. 

Multiplicación de dos funciones reales

Sean f : X → R y g : X → R dos funciones reales cualesquiera, donde X R . Entonces el producto de estas dos funciones, es decir, f ∗ g : X → R está definido por

 (f ∗ gramo) (x) = f (x) gramo (x) ∀ x ∈ X

Sean D(f) y D(g) el dominio de la función “f” y “g” respectivamente. En este caso también el dominio 

D(f * g) = D(f) D(g)

Pregunta: Dado f(x) = x ² + 1 y g(x) = 1/x. Encuentre (f ∗ g)(x). 

Solución:

(f * g)(x) = f(x) g(x) = (x2 + 1)(1/x) =  . El dominio sigue siendo el mismo que el ejemplo anterior en este caso también. 

Cociente de dos funciones reales

Sean f y g dos funciones reales definidas de X → R. El cociente de f por g se denota por   es una función definida de X → R como, 

, provided g(x) ≠ 0.

El dominio para  : {x | x ∈ re _f re _gramo y g(x) ≠ 0}

Pregunta 1: Dado f(x) = x ² + 1 y g(x) = (x + 1)/x. Encontrar 

Solución:

El dominio para f(x) es R y el dominio para g(x) es R – {0}. Además, g(x) = 0 en x = -1. 

Sabemos que el dominio debe ser {x | x ∈ Df ∩ Dg y g(x) ≠ 0 }. 

Entonces, el dominio se convierte en R – {0,1}. 

Pregunta 2: Dadas las siguientes tablas: 

X	2	4	6	8
f(x)	23	dieciséis	30	26

X	2	4	6	8
g(x)	28	32	-14	-22

Calcular: 

• (f + g)(6)
• (f-g)(8)
• (f * g)(2)
• (f/g)(4)

Responder: 

• (f + g)(6) = f (6) + g(6) = 30 + (-14) = 16
• (f – g)(8) = f (8) – g(8) = 26 – (-22) = 48
• (f * g)(2) = f (2) xg(2) = 23 x 28 = 644
• (f / g)(4) = f (4) / g(4) = 16 / 32 = ½