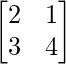
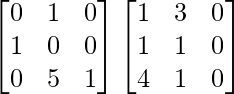
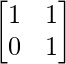
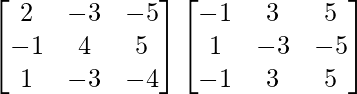
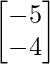
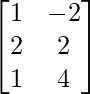
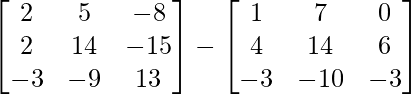
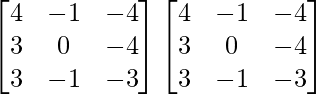
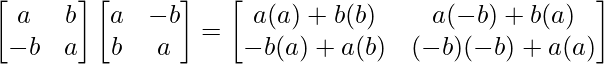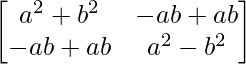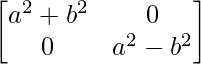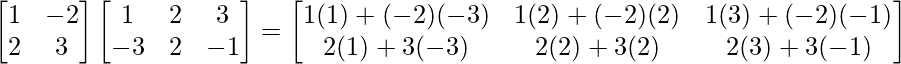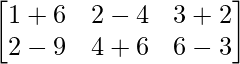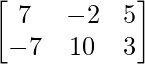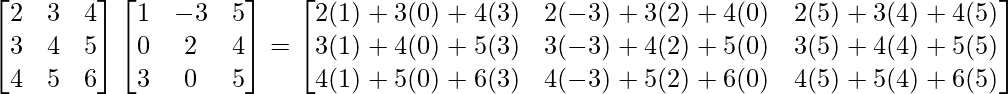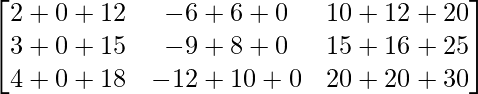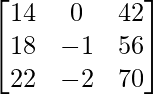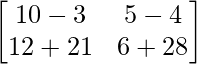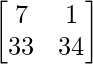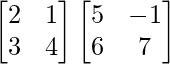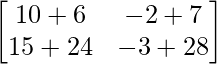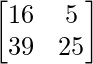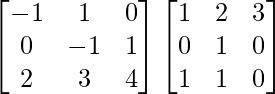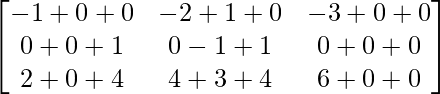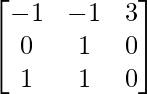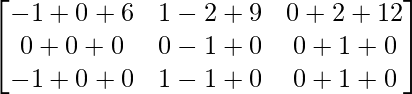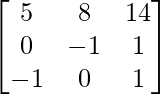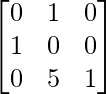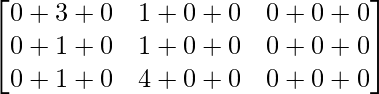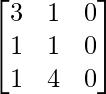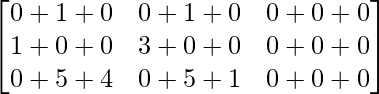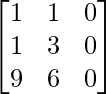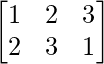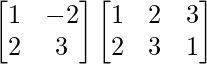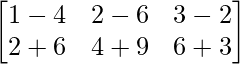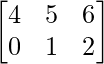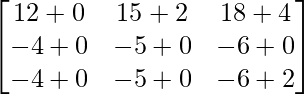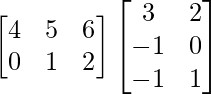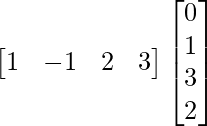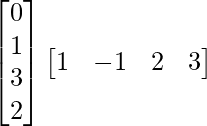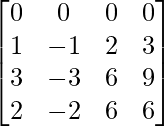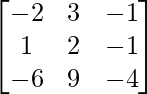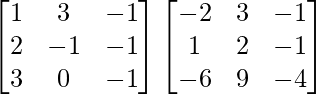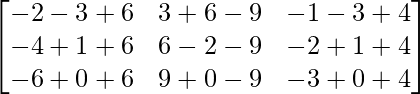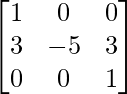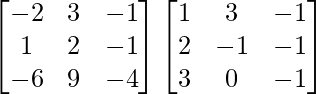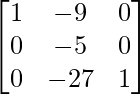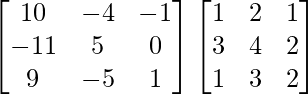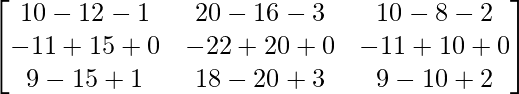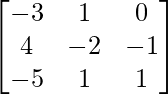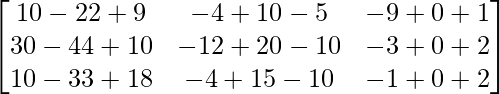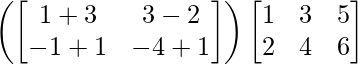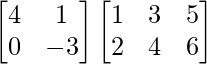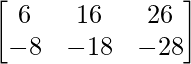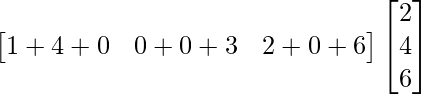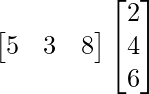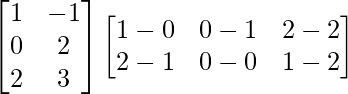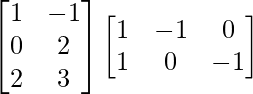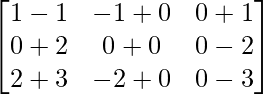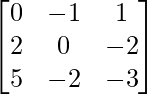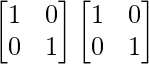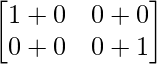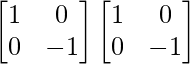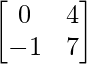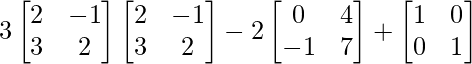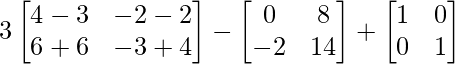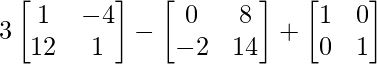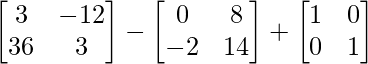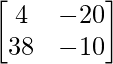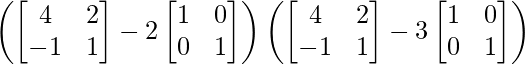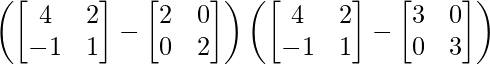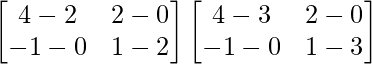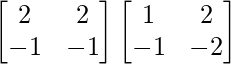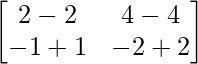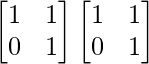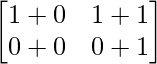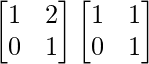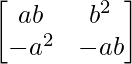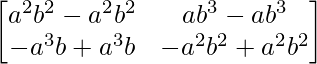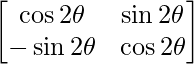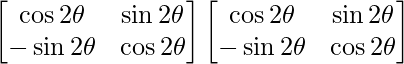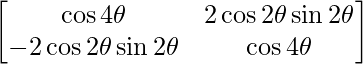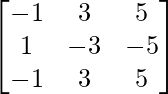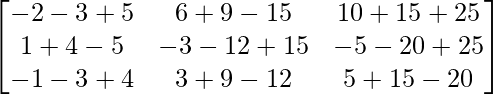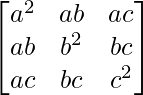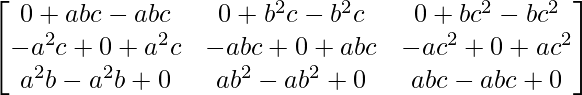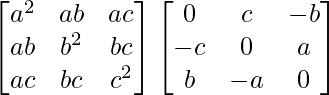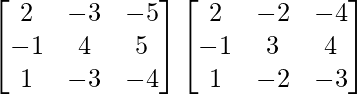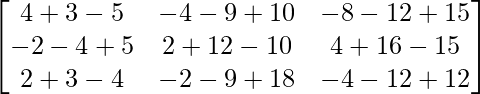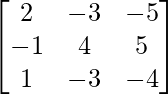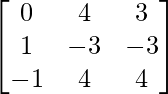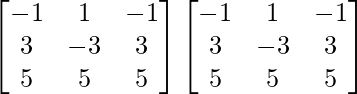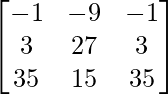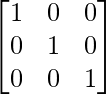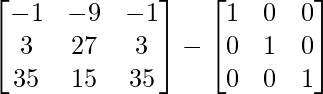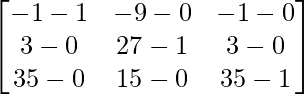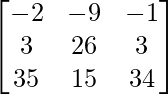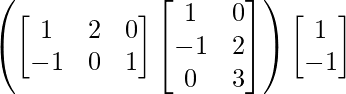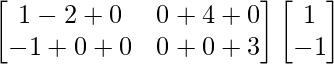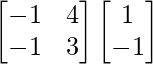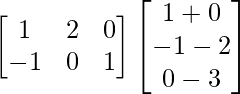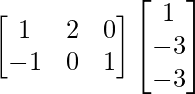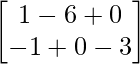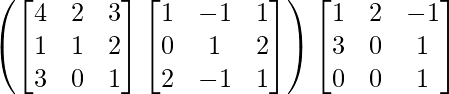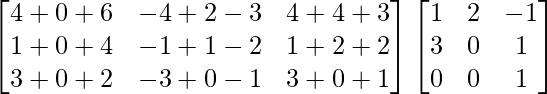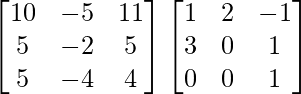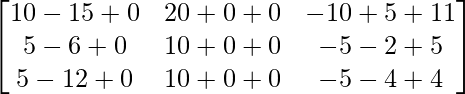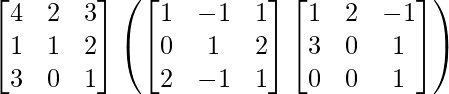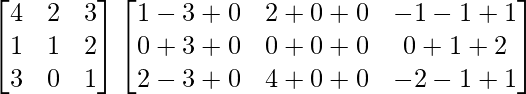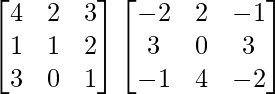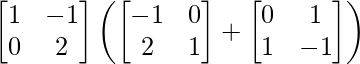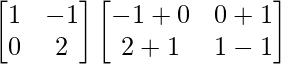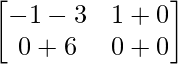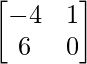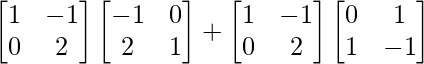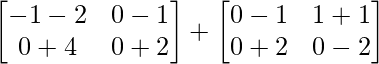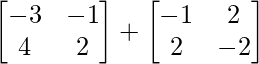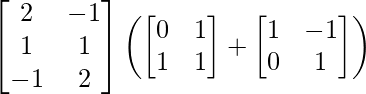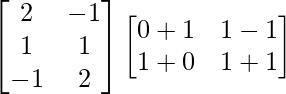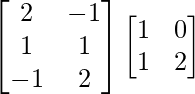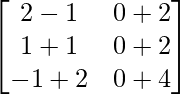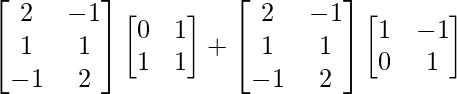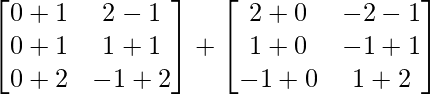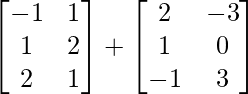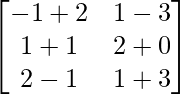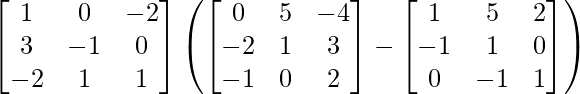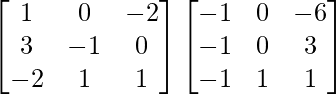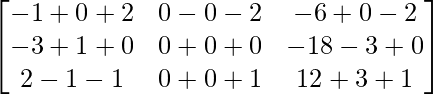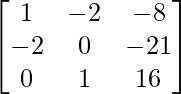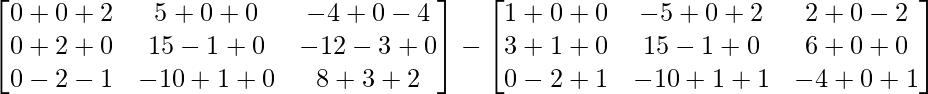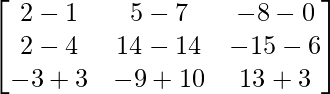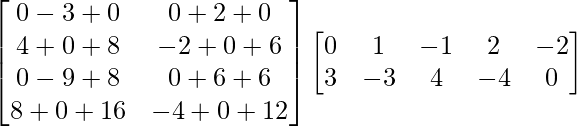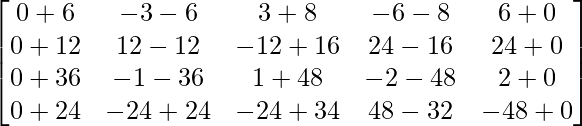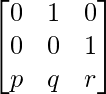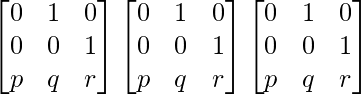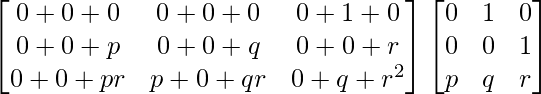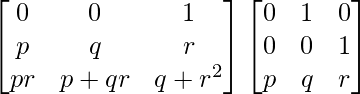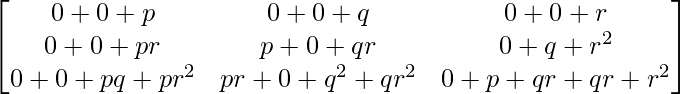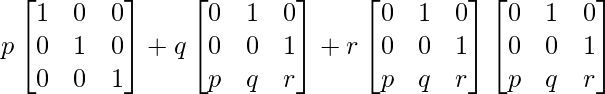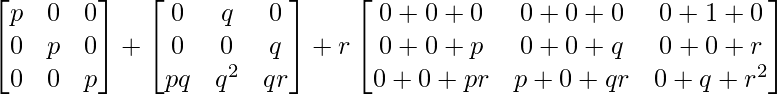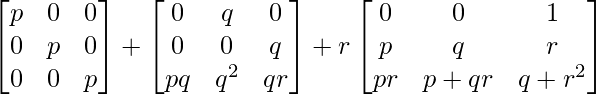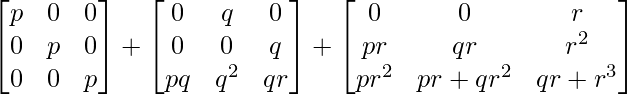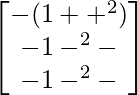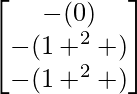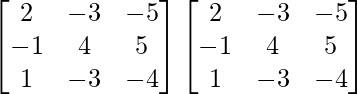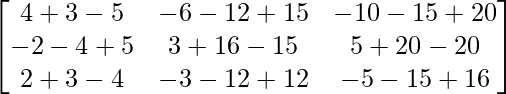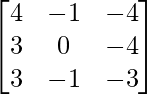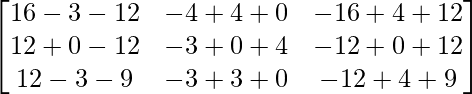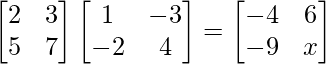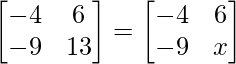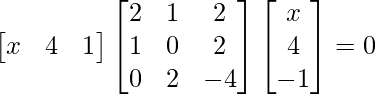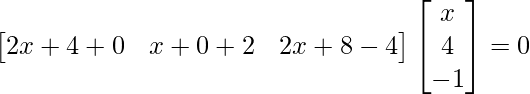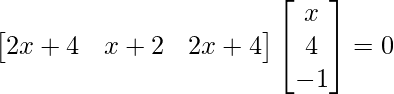Pregunta 1. Calcular los productos indicados:
(i) 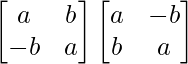
Solución:
Tenemos,
=
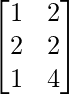
=
(ii) 
Solución:
Tenemos,
=
=
(iii) 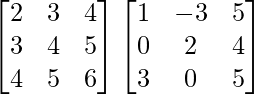
Solución:
Tenemos,
=
=
Pregunta 2. Demostrar que AB ≠ BA en cada uno de los siguientes casos:
(yo) 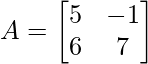 y
y 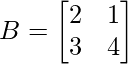
Solución:
Tenemos,
A =
y B =
AB =
=
=
Y tenemos,
BA =
=
=
Por tanto, AB ≠ BA.
Por lo tanto, probado.
(ii)  y
y 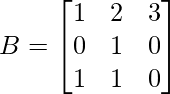
Solución:
Tenemos,
A =
y B =
AB =
=
=
Y tenemos,
BA =
=
=
Por tanto, AB ≠ BA.
Por lo tanto probado.
(iii) 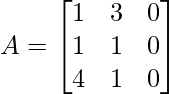 y
y 
Solución:
Tenemos,
A =
y B =
AB =
=
=
Y tenemos,
BA =
=
=
Por tanto, AB ≠ BA.
Por lo tanto probado.
Pregunta 3. Calcular los productos AB y BA el que exista en cada uno de los siguientes casos:
(yo)  y
y 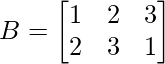
Solución:
Tenemos,
A =
y B =
Como A es de orden 2 × 2 y B es de orden 2 × 3, AB es posible pero BA no es posible.
Entonces, obtenemos
AB =
=
=
(ii) 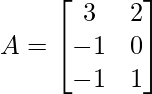 y
y 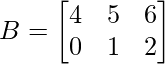
Solución:
Tenemos,
A =
y B =
Como A es de orden 3 × 2 y B es de orden 2 × 3, AB y BA son posibles.
Entonces, obtenemos,
AB =
=
=
También tenemos,
BA =
=
=
(iii) ![]() y
y 
Solución:
Tenemos,
A =
y B =
Como A es de orden 1 × 4 y B es de orden 4 × 1, AB y BA son posibles.
Entonces, obtenemos,
AB =
=
=
=
Además, tenemos,
BA =
=
=
(iv) 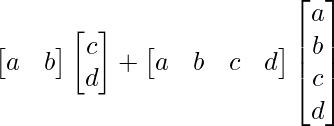
Solución:
Tenemos,
=
=
=
Pregunta 4. Demuestra que AB ≠ BA en cada uno de los siguientes casos:
(yo)  y
y 
Solución:
Tenemos,
A =
y B =
AB =
=
=
Y tenemos,
BA =
=
=
Por tanto, AB ≠ BA.
Por lo tanto probado.
(ii) 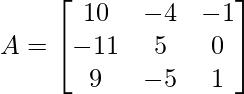 y
y 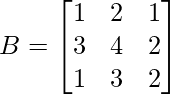
Solución:
Tenemos,
A =
y B =
AB =
=
=
Y tenemos,
BA =
=
=
Por tanto, AB ≠ BA.
Por lo tanto probado.
Pregunta 5. Evalúa lo siguiente:
(i) 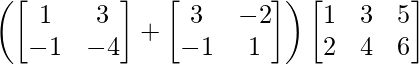
Solución:
Tenemos,
=
=
=
=
=
(ii) 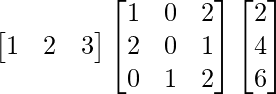
Solución:
Tenemos,
=
=
=
=
=
(iii) 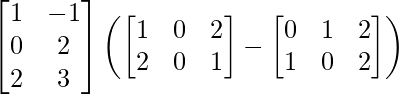
Solución:
Tenemos,
=
=
=
=
=
Pregunta 6. Si A =  , B =
, B =  y C =
y C =  , entonces demuestre que A 2 = B 2 = C 2 = I 2 .
, entonces demuestre que A 2 = B 2 = C 2 = I 2 .
Solución:
Tenemos,
A =
, B =
y C =
un 2 =
=
=
Por lo tanto, A 2 = I 2
B 2 =
=
=
Por lo tanto, B 2 = I 2
do2 = _
=
=
Por lo tanto, C 2 = I 2
Entonces, obtenemos A 2 = B 2 = C 2 = I 2
Por lo tanto probado.
Pregunta 7. Si A = 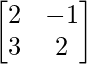 y B =
y B = 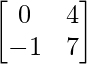 , encuentra 3A 2 – 2B + I.
, encuentra 3A 2 – 2B + I.
Solución:
Se nos da,
A =
y B =
Entonces, obtenemos,
3A 2 – 2B + I =
=
=
=
=
=
Pregunta 8. Si A = 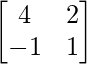 , prueba que (A – 2I) (A – 3I) = 0.
, prueba que (A – 2I) (A – 3I) = 0.
Solución:
Se nos da,
un =
IZQ = (A – 2I) (A – 3I)
=
=
=
=
=
=
= 0
= lado derecho
Por lo tanto probado.
Pregunta 9. Si A = 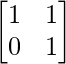 , demuestre que A 2 =
, demuestre que A 2 =  y A 3 =
y A 3 =  .
.
Solución:
Tenemos,
un =
Entonces, A 2 =
=
=
Por lo tanto, A 3 = A 2 . A
=
=
=
Por lo tanto probado.
Pregunta 10. Si A = 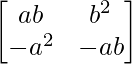 , demuestre que A 2 = 0.
, demuestre que A 2 = 0.
Solución:
Tenemos,
un =
Entonces, obtenemos
IZQ = A 2 =
=
=
= 0
= lado derecho
Por lo tanto probado.
Pregunta 11. Si A = 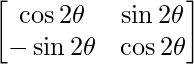 , encuentra A 2 .
, encuentra A 2 .
Solución:
Tenemos,
un =
Entonces, obtenemos
un 2 =
=
=
=
Pregunta 12. Si A = 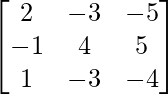 y B =
y B = 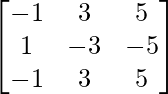 , demuestre que AB = BA = O 3×3 .
, demuestre que AB = BA = O 3×3 .
Solución:
Tenemos,
A =
y B =
Entonces, obtenemos
AB =
=
=
= O 3 × 3
Y tenemos,
BA =
=
=
= O 3 × 3
Por lo tanto, AB = BA = O 3×3 .
Por lo tanto probado.
Pregunta 13. Si A =  y B =
y B = 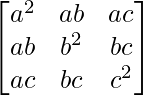 , demuestre que AB = BA = O 3×3 .
, demuestre que AB = BA = O 3×3 .
Solución:
Tenemos,
A =
y B =
Entonces tenemos,
AB =
=
=
Y tenemos,
BA =
=
=
= O 3 × 3
Por lo tanto, AB = BA = O 3×3 .
Por lo tanto probado.
Pregunta 14. Si A = 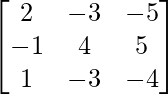 y B =
y B = 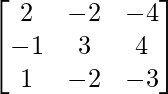 , demuestre que AB = A y BA = B.
, demuestre que AB = A y BA = B.
Solución:
Tenemos,
A =
y B =
AB =
=
=
= un
Y tenemos,
BA =
=
=
= segundo
Por lo tanto probado.
Pregunta 15. Si A =  y B =
y B = 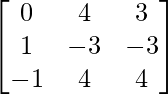 , calcule A 2 – B 2 .
, calcule A 2 – B 2 .
Solución:
Tenemos,
A =
y B =
un 2 =
=
=
Y tenemos,
B 2 =
=
=
Entonces, obtenemos
A 2 – B 2 =
=
=
Pregunta 16. Para las siguientes arrays verificar la asociatividad de la multiplicación de arrays, es decir (AB) C = A (BC).
(i) A = 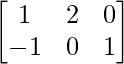 , B =
, B =  , C =
, C =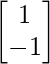
Solución:
Se nos da,
UN =
, B =
, C =
IZQ = (AB) C
=
=
=
=
Y RHS = A (BC)
=
=
=
=
=
= LHS
Por lo tanto probado.
(ii) A =  , B =
, B = 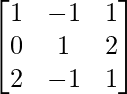 , C =
, C =
Solución:
Se nos da,
UN =
, B =
, C =
IZQ = (AB) C
=
=
=
=
=
Y RHS = A (BC)
=
=
=
=
=
= LHS
Por lo tanto probado.
Pregunta 17. Para las siguientes arrays, verifique la distributividad de la multiplicación de arrays sobre la suma de arrays, es decir, A (B + C) = AB + AC.
(i) A = 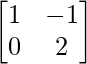 , B =
, B = 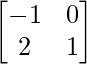 , C =
, C =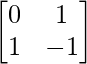
Solución:
Tenemos,
UN =
, B =
, C =
IZQ = A (B + C)
=
=
=
=
=
RHS = AB + AC
=
=
=
=
=
= LHS
Por lo tanto probado.
(ii) A = 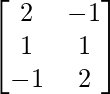 , B =
, B = 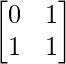 , C =
, C =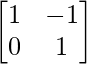
Solución:
Tenemos,
UN =
, B =
, C =
IZQ = A (B + C)
=
=
=
=
=
RHS = AB + AC
=
=
=
=
=
= LHS
Por lo tanto probado.
Pregunta 18. Si A = 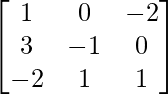 , B =
, B = 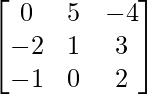 y C =
y C = 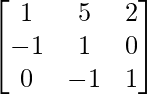 , demuestre que A (B – C) = AB – AC.
, demuestre que A (B – C) = AB – AC.
Solución:
Tenemos,
A =
, B =
y C =
IZQ = A (B – C)
=
=
=
=
=
RHS = AB – AC
=
=
=
=
=
Pregunta 19. Calcular los elementos a 43 y a 22 de la array:
un =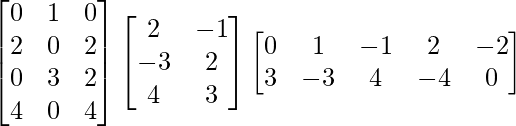
Solución:
Se nos da,
un =
=
=
=
=
Por lo tanto, un 43 = 8 y un 22 = 0.
Pregunta 20. Si A = 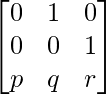 e I es la array identidad de orden 3, demuestre que A 3 = pI + qA + rA 2 .
e I es la array identidad de orden 3, demuestre que A 3 = pI + qA + rA 2 .
Solución:
Tenemos,
un =
IZQ = A 3
=
=
=
=
=
Y RHS = pI + qA + rA 2
=
=
=
=
=
=
= LHS
Por lo tanto probado.
Pregunta 21. Si ω es una raíz cúbica compleja de la unidad, demuestre que
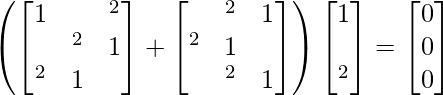
Solución:
Tenemos,
IZQ =
=
=
=
=
=
=
= lado derecho
Por lo tanto probado.
Pregunta 22. Si A = 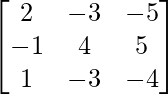 , demuestre que A 2 = A.
, demuestre que A 2 = A.
Solución:
Tenemos,
un =
Entonces, A 2 =
=
=
= un
Por lo tanto probado.
Pregunta 23. Si A =  , demuestre que A 2 = I 3 .
, demuestre que A 2 = I 3 .
Solución:
Tenemos,
un =
Entonces, A 2 =
=
=
= yo 3
Por lo tanto probado.
Pregunta 24.
(i) Si 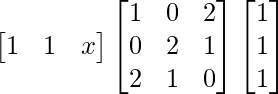 = 0, encuentre x.
= 0, encuentre x.
Solución:
Tenemos,
=>
= 0
=>
= 0
=>
= 0
=>
= 0
=> [3x + 6] = 0
=> 3x = –6
=> x = –6/3
=> x = –2
Por lo tanto, el valor de x es –2.
(ii) Si 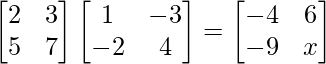 = 0, encuentre x.
= 0, encuentre x.
Solución:
Tenemos,
=>
=>
=>
Al comparar la array anterior obtenemos,
X = 13
Por lo tanto, el valor de x es –13.
Pregunta 25. Si 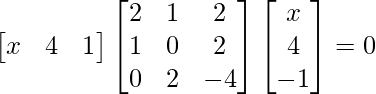 , encuentra x.
, encuentra x.
Solución:
Tenemos,
=>
=>
=>
=>
=> 2x 2 + 4x + 4x + 8 – 2x – 4 = 0
=> 2x 2 + 6x + 4 = 0
=> 2x 2 + 2x + 4x + 4 = 0
=> 2x (x + 1) + 4 (x + 1) = 0
=> (x + 1) (2x + 4) = 0
=> x = –1 o x = –2
Por lo tanto, el valor de x es -1 o -2.
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA