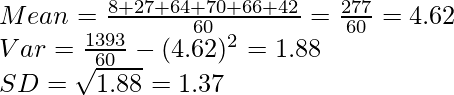Pregunta 1. Encuentra la desviación estándar para la siguiente distribución:
|
X: y: |
4.5 1 |
14.5 5 |
24,5 34,5 12 22 |
44.5 17 |
54,5 64,5 9 4 |
Solución:
X
4.5
14.5
f fx x-media
1 4,5 -33,14
5 72,5 -23,14
(x-media) 2
1098.45
535.59
f(x-media) 2
1098.45
2677.96
24.5
34.5
12 294 -13.14
22 759 -3.14
172.73
9.88
2072.82
217.31
44.5 17 756,5 6,86 47.02 799.35 54.5 9 490,5 16,86 284.16 2557.47 64.5 4 258 26,86 721.31 2885.22 N = 70 2635 12308.57 Aquí, N = 70,
Tenemos,
Pregunta 2. Calcular la media y la varianza.
|
X: y: |
0 51 |
1 2 203 383 |
3 525 |
4 532 |
5 408 |
6 273 |
7 139 |
8 9 43 27 |
10 10 |
11 4 |
12 2 |
Solución:
X
F
Fx x-media
F(x-media)
(x-media) 2
F(x-media) 2
0
1
51
203
0 -6
203 -5
-306
-1015
36
25
1836
5075
2
3
383
525
766 -4
1575 -3
-1532
-1575
dieciséis
9
6128
4725
4
5
6`
532
408
273
2128 -2
2040 -1
1638 0
-1064
-408
0
4
1
0
2128
408
0
7
8
139
43
973 1
344 2
139
86
1
4
139
172
9
10
27
10
243 3
100 4
81
40
9
dieciséis
243
160
11
12
4
2
44 5
24 6
20
12
25
36
100
72
2600
10078 -5522
21186
Aquí, N = 2600,
Ya que,
Pregunta 3. Encuentra la media y la desviación estándar de los siguientes datos:
(i)
|
Año de renderizado: Nº de personas (acumulativo) |
10 15 |
20 32 |
30 51 |
40 50 60 78 97 109 |
(ii)
|
Marcas: |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
dieciséis |
|
Frecuencia: |
1 |
6 |
6 |
8 |
8 |
2 |
2 |
3 |
0 |
2 |
1 |
0 |
0 |
0 |
1 |
Solución:
(i)
x yo
Frecuencia acumulada
yo _
arreglar yo x yo
fi x yo 2 _
10
15
15
150
1500
20
32
17
340
6800
30
51
19
570
17100
40
78
27
1080
43200
50
97
19
950
47500
60
109
12
720
43200
norte = 109
totales = 3810
totales = 159300
(ii)
x yo
yo _
arreglar yo x yo
fi x yo 2 _
2
1
2
4
3
6
18
54
4
6
24
96
5
8
40
200
6
8
48
288
7
2
14
98
8
2
dieciséis
128
9
3
27
243
10
0
0
0
11
2
22
242
12
1
12
144
13
0
0
0
14
0
0
0
15
0
0
0
dieciséis
1
dieciséis
256
norte = 40
totales = 239
totales = 1753
Pregunta 4. Encuentra la desviación estándar para los siguientes datos:
(i)
|
X: y: |
3 7 |
8 10 |
13 18 15 10 |
23 6 |
(ii)
|
X |
2 |
3 |
4 |
5 |
6 |
7 |
|
F |
4 |
9 |
dieciséis |
14 |
11 |
6 |
Solución:
(i)
x f
3 7
8 10
fx x-media (x-media) 2
21 -9,79 95,88
80 -4,79 22,96
f(x-media) 2
671.13
229.60
13 15
18 10
195 0,21 0,04
180 5,21 27,13
0,65
271.26
23 6 138 10,21 104,21 625.26 48 614 1797.92 Aquí, N = 48, y
(ii)
x yo
yo _
fi x yo 2 _
2
4
dieciséis
3
9
81
4
dieciséis
256
5
14
350
6
11
396
7
6
294
norte = 60
totales = 1393
Publicación traducida automáticamente
Artículo escrito por sudhasinghsudha90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
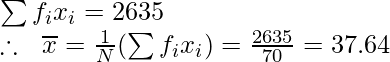
![Rendered by QuickLaTeX.com \sum f_i(x_i-\overline{x})^2 = 12308.57\\ \therefore \ \ var (x)=\frac{1}{N}\left[\sum f_i(x_i-\overline{x})^2\right]=\frac{12308.57}{70}=175.84\\ S.D. = \sqrt{var(x)}=\sqrt{175.84}=13.26](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-82128d94db2f77cf17f8cb89922f09fa_l3.png)
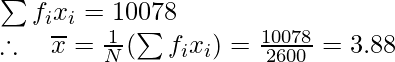
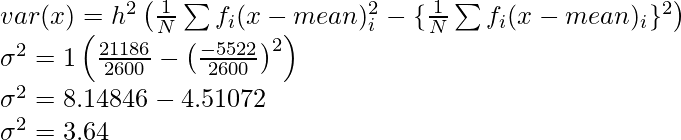
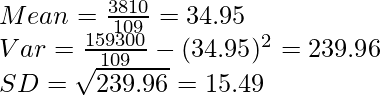
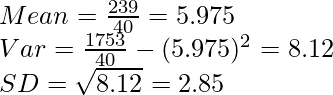
![Rendered by QuickLaTeX.com \therefore\ \ \ \overline{x}=\frac{1}{N}(\sum f_ix_i)=\frac{614}{48}=12.79\\ \sum f_i(x_i-\overline{x})^2=1797.92\\ \therefore\ \ \ \ Var(x)=\frac{1}{N}\left[\sum f_i(x_i-\overline{x})^2\right]=\frac{1797.92}{48}=37.46\\ S.D.=\sqrt{Var(x)}=\sqrt{37.46}=6.12](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-79c16461b1b1a7c87ca1fe7e9074e023_l3.png)