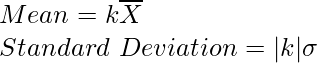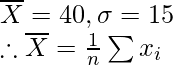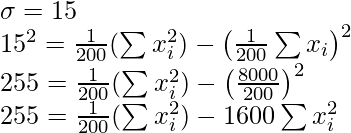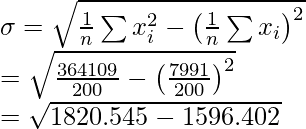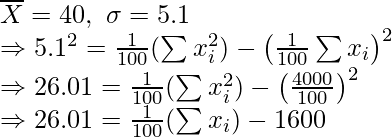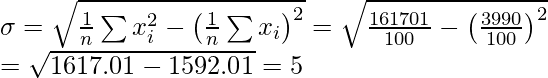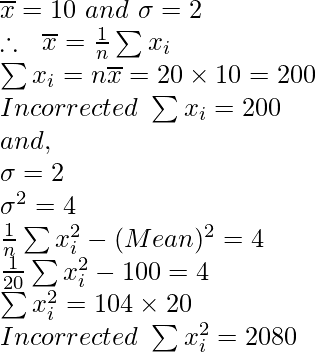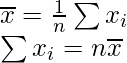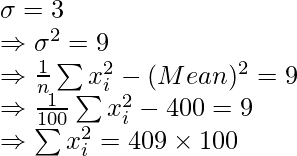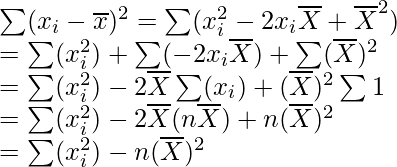Pregunta 1. Encuentra la media, la varianza y la desviación estándar de los siguientes datos:
(yo) 2, 4, 5, 6, 8, 17
(ii) 6, 7, 10, 12, 13, 4, 8, 12
(iii) 227, 235, 255, 269, 292, 299, 312, 321, 333, 348
(iv) 15, 22, 27, 11, 9, 21, 14,9
Solución:
(i)
X d = (x – Media) re 2 2 -5 25 4 -3 9 5 -2 4 6 -1 1 8 1 1 17 10 100 totales = 42 totales = 140
= 1/6[42] = 7
= 1/6[140] = 23,33
Desviación estándar = √Var(x) = √23,33 = 4,8
(ii)
X d = (x – Media) re 2 6 -3 9 7 -2 4 10 1 1 12 3 9 13 4 dieciséis 4 -5 25 8 -1 1 12 3 9 totales = 72 totales = 74 Media =
= 1/8[72] = 9
= 1/8[74] = 9,25
Desviación estándar = √Var(x) = √9,25 = 3,04
(iii)
x yo
re yo = x yo – 299
yo 2 _
227
-72
5184
235
-64
4096
255
-44
1936
269
-30
900
292
-7
49
299
0
0
312
13
169
321
22
484
333
34
1156
348
49
2401
totales = -99
totales = 16375
Media =
= 299 + (-99/10) = 289,1
= 16375/10 – (-99/10) 2
=
Desviación estándar = √Var(x) = √1539,49 = 39,24
(iv)
x yo re yo = x yo – 15 yo 2 _ 15
0
0
22
7
49
27
12
144
11
-4
dieciséis
9
-6
36
21
6
36
14
-1
1
9
-6
36
totales = 8
totales = 318
Media =
= 15 + 8/8 = 16
= 318/8 – 1 = 38,75
Desviación estándar = √Var(x) = √38,75 = 6,22
Pregunta 2. La varianza de 20 observaciones es 4. Si cada observación se multiplica por 2, encuentre la varianza de las observaciones resultantes.
Solución:
Dado: n = 20, y
Ahora multiplique cada observación por 2, obtenemos
Supongamos que X = 2x sean los nuevos datos.
=5
Entonces, para los nuevos datos, tenemos
= 4 × 5
= 20
Pregunta 3. La varianza de 15 observaciones es 4. Si cada observación se incrementa en 9, encuentre la varianza de las observaciones resultantes.
Solución:
Dado: n = 15, y
Ahora aumenta cada observación por 9, obtenemos
Supongamos que X = x + 9 sean los nuevos datos.
Así que para los nuevos datos:
= 4
Pregunta 4. La media de 5 observaciones es 4,4 y su varianza es 8,24. Si tres de las observaciones son 1, 2 y 6, encuentre las otras dos observaciones.
Solución:
Consideremos que las otras dos observaciones son x e y
Dado: La media de 5 observaciones es 4.4 y su varianza es 8.24
Asi que,
Media = 1 + 2 + 6 + x + y = 5 × 4,4
= x + y = 13
Varianza =
11,56 + 5,76 + 2,56 + (x – 4,4) 2 + (y – 4,4) 2 = 41,2
(x – 4,4) 2 + (y – 4,4) 2 = 21,32
Al resolver esta ecuación, obtenemos
(x – 4,4) 2 + (13 – x – 4,4) 2 = 21,32
(x – 4,4) 2 + (8,6 – x) 2 = 21,32
x2 – 8,8x + 19,36 + 73,96 – 17,2x + x2 = 21,32
2x 2 – 26x + 72 = 0
x 2 – 13x + 36 = 0
(x-4)(x-9) = 0
x = 4 o x = 9
Entonces, las otras dos observaciones son 4 y 9.
Pregunta 5. La media y la desviación estándar de 6 observaciones son 8 y 4 respectivamente. Si cada observación se multiplica por 3, encuentre la nueva media y la nueva desviación estándar de las observaciones resultantes.
Solución:
Dado: Media de 6 observaciones = 8
Desviación estándar de 6 observaciones = 4
k = 3
Entonces, consideremos que la media y la desviación estándar de la observación son
y
entonces la media y la Desviación Estándar de la observación multiplicada por una constante ‘k’ son
Entonces, la nueva media = 8 × 3 = 24
Nueva desviación estándar = 4 × 3 = 12
Pregunta 6. La media y la varianza de 8 observaciones son 9 y 9,25 respectivamente. Si seis de las observaciones son 6, 7, 10, 12, 12 y 13, encuentre las dos observaciones restantes.
Solución:
Dado: Media de 8 observaciones = 9
Desviación Estándar de 8 observaciones = 9.25
Observaciones = 6, 7, 10, 12, 12 y 13
Entonces, consideremos que las otras dos observaciones son x e y
Media = (6 + 7 + 10 + 12 + 12 + 13 + x + y)/8 = 9
= 60 + x + y =72
= x + y = 12 -(1)
Varianza = 1/8(6 2 + 7 2 + 10 2 + 12 2 + 12 2 + 13 2 + x 2 + y 2 ) – (81) 2 = 9,25
= 642 + x2 + y2 = 722
= x2 + y2 = 80 -(2 )
Ahora, (x + y) 2 + (x – y) 2 = 2(x 2 + y 2 )
= 144 + (x – y) 2 = 2 × 80
= (x – y) 2 = 16
= x – y = ±4
Si x – y = 4, entonces x + y = 12 y x – y = 4
Entonces, x = 8, y = 4
Si x – y = -4 entonces x + y = 12 y x – y = -4
Entonces, x = 4, y = 8
Por lo tanto, las dos observaciones restantes son 4 y 8.
Pregunta 7. Para un grupo de 200 candidatos, se encontró que las desviaciones media y estándar de las puntuaciones eran 40 y 15 respectivamente. Más tarde se descubrió que las puntuaciones de 43 y 35 se malinterpretaron como 34 y 53 respectivamente. Encuentre la media y la desviación estándar correctas.
Solución:
Dado: n = 200,
= 200 × 40 = 8000
Corregido
= Incorrecto
– (suma de valores incorrectos) + (suma de valores correctos)
= 8000 – 34 – 53 + 43 + 35 = 7991
Media corregida =
= 7991/200 = 39,955
= 200 × 1825 = 365000
Incorrecto
= 36500
Corregido
= (incorrecto
) – (suma de cuadrados de valor incorrecto) +
(suma de cuadrados de valores correctos)
= 365000 – (34) 2 – 53 2 + (43) 2 + 35 2 = 364109
Entonces, corregido
= 14,97
Pregunta 8. La media y la desviación estándar de 100 observaciones fueron calculadas como 40 y 5,1 respectivamente por un estudiante que tomó por error 50 en lugar de 40 para una observación. ¿Cuáles son la media y la desviación estándar correctas?
Solución:
Dado: n = 100,
= 100 × 1626,01 = 162601
Incorrecto = 162601
Corregido = (incorrecto) – (suma de cuadrados de valores incorrectos) + (suma de cuadrados de valores correctos)
= 162601 – (50) 2 + (40) 2 = 161701
Entonces, corregido
Pregunta 9. Se encuentra que la media y la desviación estándar de 20 observaciones son 10 y 2 respectivamente. Al volver a verificar se encontró que una observación 8 era incorrecta. Calcule la media y la desviación estándar correctas en cada uno de los siguientes casos:
(i) Si se omite un elemento incorrecto.
(ii) Si se sustituye por 12.
Solución:
Dado: n = 20,
(i) Si eliminamos 8 de la observación dada, quedan 19 observaciones.
Ahora, Incorrecto
= 200
⇒ Corregido
+ 8 = 200
⇒ Corregido
= 192
y,
⇒ Incorrecto
= 2080
⇒ Corregido
+ 8 2 = 2080
⇒ Corregido
= 2080 – 64
⇒ Corregido
= 2016
Por lo tanto,
Media corregida =
= 10,10
⇒ Entonces, varianza corregida =
= 2016/19 – (192/19) 2
= (38304 -36864)/361
= 1440/361
Entonces, la desviación estándar corregida =
= 1.997
(ii) Si reemplazamos la observación incorrecta (es decir, 8) por 12
Dado: Incorrecto
= 200
Por lo tanto, Corregido
= 200 – 8 + 12 = 204
Incorrecto
= 2080
Por lo tanto, Corregido
= 2080 – 8 2 + 12 2 = 2160
Ahora, media corregida = 204/20 = 10,2
Varianza corregida =
= 2016/20 – (204/20) 2
=
=
= 1584/400
Entonces, la desviación estándar corregida =
= 19,899/10 = 1,9899
Pregunta 10. Se encontró que la media y la desviación estándar del grupo de 100 observaciones eran 20 y 3 respectivamente. Más tarde se encontró que tres observaciones eran incorrectas, las cuales se registraron como 21, 21 y 18. Halle la media y la desviación estándar si se omitió la observación incorrecta.
Solución:
(i) Dado: n = 100,
Media =
= 20 × 100 = 2000
Incorrecto
= 2000
y,
Incorrecto
= 40900.
Cuando las observaciones incorrectas 21, 21, 18 se eliminan de los datos
entonces el número total de observaciones es n = 97
Ahora,
Incorrecto
= 2000
Corregido
= 2000 – 21 – 21 – 18 = 1940
y,
Incorrecto
= 40900
Corregido
= 40900 – 21 2 – 21 2 – 18 2
= 40900 – 1206
= 39694
Por lo tanto, Media corregida = 1940/97 = 20
Varianza corregida =
= (39694/97) – (20) 2 = 409,22 – 400 = 9,22
Entonces, la desviación estándar corregida = √9.22 = 3.04
Pregunta 11. Muestre que las dos fórmulas para la desviación estándar de datos no agrupados
son equivalentes, donde 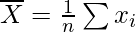
Solución:
Dado:
Al dividir ambos lados por n obtenemos,
Ahora, sacando raíces cuadradas en ambos lados, obtenemos
Publicación traducida automáticamente
Artículo escrito por yashkumar0457 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
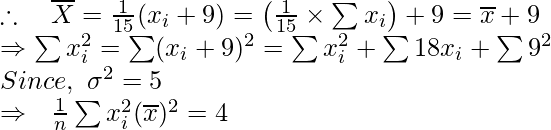
![Rendered by QuickLaTeX.com \sigma^2=\frac{1}{n}\sum X_i^2-(\overline{X})^2=\frac{1}{15}(\sum x_i^2+\sum18x_i+\sum9^2)-(\overline{x}+9)^2\\ =\frac{1}{15}\sum x_i^2+15\sum18x_i+\frac{1}{15}\sum9^2-(9)^2-(18\overline{x})-(\overline{x})^2\\ =\left[\frac{1}{15}\sum x_i-(\overline{x})^2\right]+\left[\frac{1}{15}\sum18x_i-(18\overline{x})\right]+\left[\frac{1}{15}\sum9^2-(9)^2\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d2461298b4fff891d8300b5cb4a211e0_l3.png)
![Rendered by QuickLaTeX.com =\left[\frac{1}{15}\sum x_i^2-(\overline{x})^2\right]+\left[18\times\frac{1}{15}\sum x_i-(18\overline{x})\right]+\left[\frac{1}{15}\times15\times(9)^2-(9)^2\right]\\ \frac{1}{15}\sum x_i^2-(\overline{x})^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3f0686bf95c912a235c48120bea74338_l3.png)