Cree un DFA para aceptar una string binaria que contenga «01» i veces y «1» 2j veces

Posted on by Rudeus Greyrat

Dada una string binaria str , la tarea es construir un DFA que acepte una string binaria dada si contiene «01» i veces y «1» 2j veces, es decir, 

L={(01)^i (1)^{2j} \text{ where }i\geq1\text{ and }j\geq1}
 

Ejemplos: 

Entrada: str = “011111” 
Salida: Aceptada 
Explicación: 
La string sigue al idioma como: (01) 1 (1) 2*2

Entrada: str = “01111” 
Salida: No aceptado

DFA o Deterministic Finite Automata es una máquina de estado finito que acepta una string (bajo alguna condición específica) si alcanza un estado final, de lo contrario la rechaza.
En DFA, no existe el concepto de memoria, por lo tanto, debemos verificar la string carácter por carácter, comenzando con el carácter 0. El conjunto de caracteres de entrada para el problema es {0, 1}. Para que un DFA sea válido, debe haber una regla de transición definida para cada símbolo del conjunto de entrada en cada estado a un estado válido. Por lo tanto, se siguen los siguientes pasos para diseñar el DFA:

  1. Cree la etapa inicial y haga la transición de 0 y 1 al siguiente estado posible.
  2. La transición de 0 siempre es seguida por la transición de 1.
  3. Haga un estado inicial y transite sus alfabetos de entrada, es decir, 0 y 1 a dos estados diferentes.
  4. Verifique la aceptación de la string después de cada transición para ignorar los errores.
  5. Primero, haga DfA para una string de longitud mínima y luego avance paso a paso.
  6. Defina los estados finales de acuerdo con la aceptación de la string.

Enfoque paso a paso para diseñar un DFA:  

  • Paso 1: La string mínima aceptable posible es 0111, es decir, (01) 1 (11) 1 . Por lo tanto, cree un estado inicial «A» que haga la transición de 0 al estado «B» y luego la transición de 1 de «B» al estado «C», luego la transición de 1 de «C» a «D», luego la transición de 1 de «D» a «E» como se muestra en el diagrama, esta etapa «E» es el estado final.

  • Paso 2: Ahora, piense en la string que tiene un (01) consecutivo y luego un (11) consecutivo para terminar la string. Por lo tanto, cuando i>1, haga una transición de «0» del estado «C» al estado «B» y haga una transición de «1» del estado «E» al estado «D». Por lo tanto, ahora se aceptan strings como 010111, 011111, 0101111111, etc.

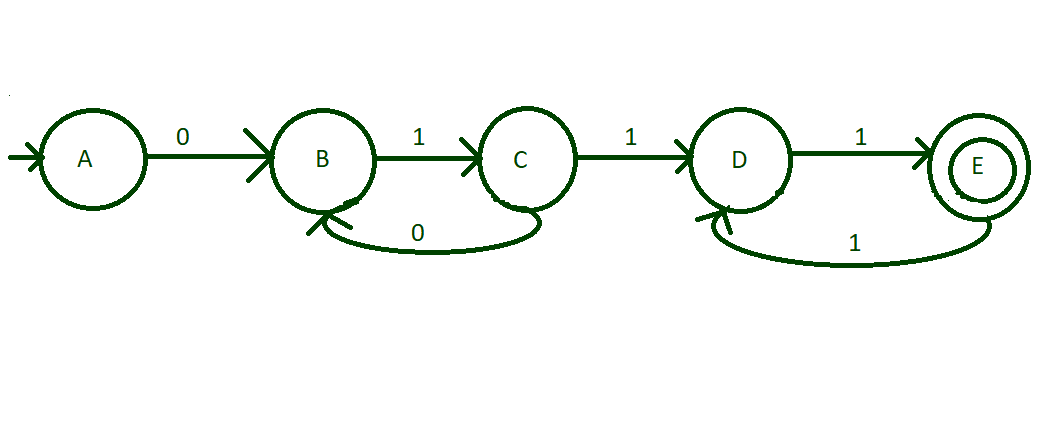
  • Paso 3: Lo hemos hecho con todo tipo de strings posibles de aceptar. Sin embargo, hay pocos alfabetos de entrada que no se transfieran a ninguno de los estados. En este caso, todo este tipo de entrada se enviará a algún estado muerto para bloquear sus transiciones adicionales que no son aceptables. Los alfabetos de entrada del estado inactivo se enviarán al propio estado inactivo. Por lo tanto, el diseño final del DFA es:

A continuación se muestra la implementación del enfoque anterior: 

Java

// Java code for the above DFA
import java.util.*;
 
class GFG{
   
// Function for the state A
static void checkstatea(String n)
{
  if (n.length() % 2 != 0 ||
      n.length() < 4)
    System.out.print("string not accepted");
  else
  {   
    int i = 0;
     
    // State transition to B
    // if the character is 0
    if (n.charAt(i) == '0')
      stateb(n.substring(1));
    else
      System.out.print("string not accepted");
  }
}
  
// Function for the state B
static void stateb(String n)
{
  int i = 0;
   
  if (n.charAt(i) == '0')
    System.out.print("string not accepted");
  
  // State transition to C
  // if the character is 1
  else
    statec(n.substring(1));
}
   
// Function for the state C
static void statec(String n)
{
  int i = 0;
   
  // State transition to D
  // if the character is 1
  if (n.charAt(i) == '1')
    stated(n.substring(1));
  
  // State transition to B
  // if the character is 0
  else
    stateb(n.substring(1));
}
  
// Function for the state D
static void stated(String n)
{
  int i = 0;
   
  if (n.length() == 1)
  {
    if (n.charAt(i) == '1')
      System.out.print("string accepted");
    else
      System.out.print("string not accepted");
  }
  else
  {
     
    // State transition to E
    // if the character is 1
    if (n.charAt(i) == '1')
      statee(n.substring(1));
    else
      System.out.print("string not accepted");
  }
}
  
// Function for the state E    
static void statee(String n)
{
  int i = 0;
   
  if (n.length() == 1)
  {
    if (n.charAt(i) == '0')
      System.out.print("string not accepted");
    else
      System.out.print("string accepted");
  }
  else
  {
    if (n.charAt(i) == '0')
      System.out.print("string not accepted");
     
    stated(n.substring(1));
  }
}
      
// Driver code
public static void main(String []args)
{
   
  // Take string input
  String n ="011111";
  
  // Call stateA to check the input
  checkstatea(n);
}
}
 
// This code is contributed by pratham76

Python3

# Python3 program for the given
# language
 
# Function for the state A
def checkstatea(n):
    if(len(n)%2!=0 or len(n)<4):
        print("string not accepted")
    else:   
        i=0
 
        # State transition to B
        # if the character is 0
        if(n[i]=='0'):
            stateb(n[1:])
        else:
            print("string not accepted")
 
# Function for the state B
def stateb(n):
    i=0
    if(n[i]=='0'):
        print("string not accepted")
 
    # State transition to C
    # if the character is 1
    else:
        statec(n[1:])
 
# Function for the state C
def statec(n):
    i=0
 
    # State transition to D
    # if the character is 1
    if(n[i]=='1'):
        stated(n[1:])
 
    # State transition to B
    # if the character is 0
    else:
        stateb(n[1:])
 
# Function for the state D
def stated(n):
    i=0
    if(len(n)==1):
        if(n[i]=='1'):
            print("string accepted")
        else:
            print("string not accepted")
    else:
 
        # State transition to E
        # if the character is 1
        if(n[i]=='1'):
            statee(n[1:])
        else:
            print("string not accepted")  
 
# Function for the state E    
def statee(n):
    i=0
    if(len(n)==1):
        if(n[i]=='0'):
            print("string not accepted")
        else:
            print("string accepted")
          
    else:
        if(n[i]=='0'):
            print("string not accepted")
        stated(n[1:])
      
      
# Driver code
if __name__ == "__main__":
 
    n = "011111"
    checkstatea(n)
    

C#

// C# code for the above DFA
using System;
using System.Collections;
using System.Collections.Generic;
class GFG{
     
// Function for the state A
static void checkstatea(string n)
{
  if(n.Length % 2 != 0 ||
     n.Length < 4)
    Console.Write("string not accepted");
  else
  {   
    int i = 0;
 
    // State transition to B
    // if the character is 0
    if(n[i] == '0')
      stateb(n.Substring(1));
    else
      Console.Write("string not accepted");
  }
}
 
// Function for the state B
static void stateb(string n)
{
  int i = 0;
  if(n[i] == '0')
    Console.Write("string not accepted");
 
  // State transition to C
  // if the character is 1
  else
    statec(n.Substring(1));
}
  
// Function for the state C
static void statec(string n)
{
  int i = 0;
 
  // State transition to D
  // if the character is 1
  if(n[i] == '1')
    stated(n.Substring(1));
 
  // State transition to B
  // if the character is 0
  else
    stateb(n.Substring(1));
}
 
// Function for the state D
static void stated(string n)
{
  int i = 0;
  if(n.Length == 1)
  {
    if(n[i] == '1')
      Console.Write("string accepted");
    else
      Console.Write("string not accepted");
  }
  else
  {
    // State transition to E
    // if the character is 1
    if(n[i] == '1')
      statee(n.Substring(1));
    else
      Console.Write("string not accepted");
  }
}
 
// Function for the state E    
static void statee(string n)
{
  int i = 0;
  if(n.Length == 1)
  {
    if(n[i] == '0')
      Console.Write("string not accepted");
    else
      Console.Write("string accepted");
  }
  else
  {
    if(n[i] == '0')
      Console.Write("string not accepted");
    stated(n.Substring(1));
  }
}
     
// Driver code
public static void Main(string []args)
{
  // Take string input
  string n ="011111";
 
  // Call stateA to check the input
  checkstatea(n);
}
}
 
// This code is contributed by rutvik_56

Javascript

<script>
 
      // JavaScript code for the above DFA
      // Function for the state A
      function checkstatea(n) {
        if (n.length % 2 !== 0 || n.length < 4)
          document.write("string not accepted");
        else {
          var i = 0;
 
          // State transition to B
          // if the character is 0
          if (n[i] === "0") stateb(n.substring(1));
          else document.write("string not accepted");
        }
      }
 
      // Function for the state B
      function stateb(n) {
        var i = 0;
        if (n[i] === "0") document.write("string not accepted");
        // State transition to C
        // if the character is 1
        else statec(n.substring(1));
      }
 
      // Function for the state C
      function statec(n) {
        var i = 0;
 
        // State transition to D
        // if the character is 1
        if (n[i] === "1") stated(n.substring(1));
        // State transition to B
        // if the character is 0
        else stateb(n.substring(1));
      }
 
      // Function for the state D
      function stated(n) {
        var i = 0;
        if (n.length === 1) {
          if (n[i] === "1") document.write("string accepted");
          else document.write("string not accepted");
        } else {
          // State transition to E
          // if the character is 1
          if (n[i] === "1") statee(n.substring(1));
          else document.write("string not accepted");
        }
      }
 
      // Function for the state E
      function statee(n) {
        var i = 0;
        if (n.length == 1) {
          if (n[i] === "0") document.write("string not accepted");
          else document.write("string accepted");
        } else {
          if (n[i] === "0") document.write("string not accepted");
          stated(n.substring(1));
        }
      }
 
      // Driver code
      // Take string input
      var n = "011111";
 
      // Call stateA to check the input
      checkstatea(n);
       
</script>
Producción: 

string accepted

 

Publicación traducida automáticamente

Artículo escrito por _mridul_bhardwaj_ y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *