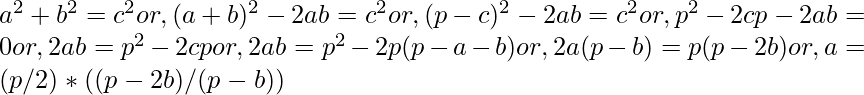Dado un perímetro P, la tarea es encontrar el número de triángulos rectángulos posibles con perímetro igual a p.
Ejemplos:
Input: P = 12 Output: number of right triangles = 1 The only right angle possible is with sides hypotenuse = 5, perpendicular = 4 and base = 3. Input: p = 840 Output: number of right triangles = 8
Entonces, el objetivo es encontrar el número de soluciones que satisfagan las ecuaciones a + b + c = p y a 2 + b 2 = c 2 .
Un enfoque ingenuo es ejecutar dos bucles para a(1 a p/2) y b(a+1 a p/3) y luego hacer c=pab y aumentar la cuenta en uno si ![]() . Esto llevará
. Esto llevará ![]() tiempo.
tiempo.
Se puede encontrar un enfoque eficiente mediante una pequeña manipulación algebraica:
Dado que a + c > bo, p – b > bo, b < p/2. Por lo tanto, iterar b de 1 a p/2, calcular a y almacenar solo el número entero a daría todas las soluciones para un p dado. No hay triángulos rectángulos posibles para p impar ya que los triángulos de ángulo recto siguen el teorema de Pitágoras . Use una lista de pares para almacenar los valores de a y band devuelva el conteo al final.
A continuación se muestra la implementación del enfoque anterior.
C++
// C++ program to find the number of
// right triangles with given perimeter
#include<bits/stdc++.h>
using namespace std;
// Function to return the count
int countTriangles(int p)
{
// making a list to store (a, b) pairs
vector<pair<int,int>> store;
// no triangle if p is odd
if (p % 2 != 0)
return 0;
else
{
int count = 1;
for(int b = 1; b < p / 2; b++)
{
float a = (float)p / 2.0f * ((float)((float)p -
2.0 * (float)b) /
((float)p - (float)b));
int inta = (int)(a);
if (a == inta)
{
// make (a, b) pair in sorted order
pair<int,int> ab;
if(inta<b)
{
ab = {inta, b};
}
else
{
ab = {b, inta};
}
// check to avoid duplicates
if(find(store.begin(), store.end(), ab) == store.end())
{
count += 1;
// store the new pair
store.push_back(ab);
}
}
}
return count;
}
}
// Driver Code
int main()
{
int p = 840;
cout << "number of right triangles = " << countTriangles(p);
return 0;
}
// This code is contributed by rutvik_56.
Java
// Java program to find the number of
// right triangles with given perimeter
import java.util.*;
class GFG{
static class pair
{
int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
// Function to return the count
static int countTriangles(int p)
{
// making a list to store (a, b) pairs
HashSet<pair> store = new HashSet<pair>();
// no triangle if p is odd
if (p % 2 != 0)
return 0;
else
{
int count = 1;
for(int b = 1; b < p / 3; b++)
{
float a = (float)p / 2.0f * ((float)((float)p -
2.0 * (float)b) /
((float)p - (float)b));
int inta = (int)(a);
if (a == inta)
{
// make (a, b) pair in sorted order
pair ab;
if(inta<b)
{
ab = new pair(inta, b);
}
else
{
ab = new pair(b, inta);
}
// check to astatic void duplicates
if(!store.contains(ab) )
{
count += 1;
// store the new pair
store.add(ab);
}
}
}
return count;
}
}
// Driver Code
public static void main(String[] args)
{
int p = 840;
System.out.print("number of right triangles = " + countTriangles(p));
}
}
// This code is contributed by Rajput-Ji
Python3
# python program to find the number of
# right triangles with given perimeter
# Function to return the count
def countTriangles(p):
# making a list to store (a, b) pairs
store =[]
# no triangle if p is odd
if p % 2 != 0 : return 0
else :
count = 0
for b in range(1, p // 2):
a = p / 2 * ((p - 2 * b) / (p - b))
inta = int(a)
if (a == inta ):
# make (a, b) pair in sorted order
ab = tuple(sorted((inta, b)))
# check to avoid duplicates
if ab not in store :
count += 1
# store the new pair
store.append(ab)
return count
# Driver Code
p = 840
print("number of right triangles = "+str(countTriangles(p)))
C#
// C# program to find the number of
// right triangles with given perimeter
using System;
using System.Collections.Generic;
public class GFG {
public class pair {
public int first, second;
public pair(int first, int second) {
this.first = first;
this.second = second;
}
}
// Function to return the count
static int countTriangles(int p)
{
// making a list to store (a, b) pairs
HashSet<pair> store = new HashSet<pair>();
// no triangle if p is odd
if (p % 2 != 0)
return 0;
else {
int count = 1;
for (int b = 1; b < p / 3; b++) {
float a = (float) p / 3 * ((float) ((float) p -
2 * (float) b) /
((float) p - (float) b));
int inta = (int) (a);
if (a == inta)
{
// make (a, b) pair in sorted order
pair ab;
if (inta < b) {
ab = new pair(inta, b);
} else {
ab = new pair(b, inta);
}
// check to astatic void duplicates
if (!store.Contains(ab)) {
count += 1;
// store the new pair
store.Add(ab);
}
}
}
return count;
}
}
// Driver Code
public static void Main(String[] args) {
int p = 840;
Console.Write("number of right triangles = " + countTriangles(p));
}
}
// This code is contributed by gauravrajput1
Javascript
<script>
// Javascript program to find the number of
// right triangles with given perimeter
class pair {
constructor(first , second) {
this.first = first;
this.second = second;
}
}
// Function to return the count
function countTriangles(p)
{
// making a list to store (a, b) pairs
var store = new Set();
// no triangle if p is odd
if (p % 2 != 0)
return 0;
else {
var count = 1;
for (var b = 1; b < p / 3; b++) {
var a = p / 3 * ( ( p - 2 * b) / ( p - b));
var inta = parseInt( a);
if (a == inta) {
// make (a, b) pair in sorted order
var ab;
if (inta < b) {
ab = new pair(inta, b);
} else {
ab = new pair(b, inta);
}
// check to afunction duplicates
if (!store.has(ab)) {
count += 1;
// store the new pair
store.add(ab);
}
}
}
return count;
}
}
// Driver Code
var p = 840;
document.write("number of right triangles = " + countTriangles(p));
// This code is contributed by Rajput-Ji
</script>
number of right triangles = 8
Complejidad del tiempo: O(P)
Complejidad del espacio : O(n) como espacio auxiliar se está utilizando
Publicación traducida automáticamente
Artículo escrito por SujanDutta y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA