Hay 
personas que se van a agrupar en equipos exactamente 
de modo que haya al menos una persona en cada equipo. Todos los miembros de un equipo son amigos entre sí. Encuentre el número mínimo y máximo. de parejas de amigos que se pueden formar agrupando a estas personas en equipos exactamente . Ejemplos:
Entrada : 5 2
Salida : 4 6
Para máximo no. de parejas, el primer equipo contiene solo 1 miembro y el segundo equipo contiene 4 personas que son amigas entre sí, por lo que no. de parejas en 1er equipo + núm. de parejas en 2do equipo = 0 + 6 = total de parejas = 6
Para mínimo no. de parejas, el 1er equipo contiene 2 miembros y el 2do equipo contiene 3 personas que son amigas entre sí, entonces no. de parejas en 1er equipo + núm. de parejas en el 2do equipo = 1 + 3 = total de parejas = 4
Entrada : 2 1
Salida : 1 1
Explicación:
Primero que nada, tenemos que poner 1 miembro en cada equipo para satisfacer la restricción. Así que nos quedamos con la 
gente.
1. Para el número máximo de pares
Se puede ver que máximo no. Los pares pueden resultar solo poniendo a todos los miembros restantes del mismo equipo. Se puede explicar de la siguiente manera:
Considere 2 equipos, uno que contiene x personas y otro que contiene 1 persona, ahora tenemos que agregar 1 persona más a ambos equipos, agregarlo al equipo de x personas aumenta el no. de pares por x mientras que agregarlo al otro equipo solo aumenta el no. de pares por 1. Por lo tanto, para el máximo no. de parejas, tenemos que poner a todas las personas restantes en un mismo equipo.
Ahora la distribución de equipos para el máximo no. de pares sería algo así: 
Por lo tanto,
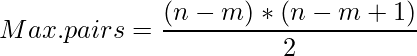
Ej: Si un equipo consta de 3 personas, la 3ra persona tiene 1 y 2 como amigos, la 2da persona tiene 1 como amigo. Por lo tanto, 2+1 = ((3-1)*(3))/2 amigos
2. Para mínimo no. de pares
Ahora de la misma explicación, se puede ver que mínimo no. de parejas se obtienen cuando todas las personas se distribuyen por igual en los equipos. Por lo tanto, los nm de personas restantes deben distribuirse en m equipos, de modo que cada equipo contenga (nm)/m de personas más. Ahora quedan 
personas que deben llenarse 1 en cada equipo (se puede ver contrario a la condición anterior de máximo).
Ahora la distribución del equipo para el número mínimo. de pares sería algo así:
Cada equipo tiene 
miembros y los equipos tienen un miembro extra.
Así que total no. de parejas = Nº total de parejas en m equipos cada uno de tamaño 
+ Nº de parejas formadas al sumar 1 persona en equipos que tienen tamaño
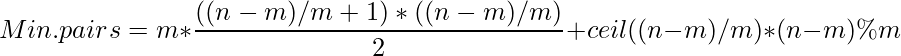
C++
// CPP program to find minimum and maximum no. of pairs
#include <bits/stdc++.h>
using namespace std;
void MinimumMaximumPairs(int n, int m)
{
int max_pairs = ((n - m + 1) * (n - m)) / 2;
int min_pairs = m * (((n - m) / m + 1) * ((n - m) / m)) / 2 +
ceil((n - m) / double(m)) * ((n - m) % m);
cout << "Minimum no. of pairs = " << min_pairs << "\n";
cout << "Maximum no. of pairs = " << max_pairs << "\n";
}
// Driver code
int main()
{
int n = 5, m = 2;
MinimumMaximumPairs(n, m);
return 0;
}
Java
//Java program to find minimum
// and maximum no. of pairs
import java.io.*;
class GFG {
static void MinimumMaximumPairs(int n, int m)
{
int max_pairs = ((n - m + 1) * (n - m)) / 2;
int min_pairs = m * (((n - m) / m + 1) * ((n - m) / m)) / 2 +
(int)Math.ceil((double)((n - m) /
(double)(m))) * ((n - m) % m);
System.out.println("Minimum no. of pairs = " + min_pairs);
System.out.println("Maximum no. of pairs = " + max_pairs);
}
// Driver code
public static void main (String[] args) {
int n = 5, m = 2;
MinimumMaximumPairs(n, m);
}
}
// This code is contributed by Sachin.
Python3
# Python3 program to find minimum
# and maximum no. of pairs
from math import ceil
def MinimumMaximumPairs(n, m) :
max_pairs = ((n - m + 1) * (n - m)) // 2;
min_pairs = (m * (((n - m) // m + 1) *
((n - m) // m)) // 2 +
ceil((n - m) / (m)) *
((n - m) % m))
print("Minimum no. of pairs = ", min_pairs)
print("Maximum no. of pairs = " , max_pairs)
# Driver code
if __name__ == "__main__" :
n ,m= 5, 2
MinimumMaximumPairs(n, m)
# This code is contributed by Ryuga
C#
// C# program to find minimum
// and maximum no. of pairs
using System;
class GFG
{
static void MinimumMaximumPairs(int n, int m)
{
int max_pairs = ((n - m + 1) * (n - m)) / 2;
int min_pairs = m * (((n - m) / m + 1) * ((n - m) / m)) / 2 +
(int)Math.Ceiling((double)((n - m) /
(double)(m))) * ((n - m) % m);
Console.WriteLine("Minimum no. of pairs = " + min_pairs);
Console.WriteLine("Maximum no. of pairs = " + max_pairs);
}
// Driver code
public static void Main()
{
int n = 5, m = 2;
MinimumMaximumPairs(n, m);
}
}
// This code is contributed by Akanksha Rai
PHP
<?php
// PHP program to find minimum
// and maximum no. of pairs
function MinimumMaximumPairs($n, $m)
{
$max_pairs = (($n - $m + 1) * ($n - $m)) / 2;
$min_pairs = $m * (int)((((int)($n - $m) / $m + 1) *
((int)($n - $m) / $m)) / 2) +
(int)ceil(($n - $m) / $m) *
(($n - $m) % $m);
echo("Minimum no. of pairs = " .
"$min_pairs" . "\n");
echo("Maximum no. of pairs = " .
"$max_pairs");
}
// Driver code
$n = 5; $m = 2;
MinimumMaximumPairs($n, $m);
// This code is contributed
// by Mukul Singh
?>
Javascript
<script>
// javascript program to find minimum
// and maximum no. of pairs
function MinimumMaximumPairs(n, m)
{
var max_pairs = parseInt(((n - m + 1) * (n - m)) / 2);
var min_pairs = m * parseInt((((n - m) / m + 1) * ((n - m) / m)) / 2)
+ parseInt( Math.ceil(((n - m) / (m)))) * ((n - m) % m);
document.write("Minimum no. of pairs = " + min_pairs+"<br/>");
document.write("Maximum no. of pairs = " + max_pairs);
}
// Driver code
var n = 5, m = 2;
MinimumMaximumPairs(n, m);
// This code is contributed by gauravrajput1
</script>
Producción
Minimum no. of pairs = 4 Maximum no. of pairs = 6
Complejidad del tiempo: 
Espacio Auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por sanskar27jain y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA