Agrupamiento en Programación R

La agrupación en clústeres en el lenguaje de programación R es una técnica de aprendizaje no supervisada en la que el conjunto de datos se divide en varios grupos denominados clústeres en función de su similitud. Varios grupos de datos se producen después de la segmentación de datos. Todos los objetos de un clúster comparten características comunes. Durante la extracción y el análisis de datos, la agrupación se utiliza para encontrar conjuntos de datos similares.

Aplicaciones de la agrupación en lenguaje de programación R

• Marketing: en la programación R, la agrupación en clústeres es útil para el campo del marketing. Ayuda a encontrar el patrón del mercado y, por lo tanto, ayuda a encontrar posibles compradores. Obtener los intereses de los clientes mediante la agrupación y mostrar el mismo producto de su interés puede aumentar la posibilidad de comprar el producto.
• Ciencia Médica: En el campo de la medicina, hay una nueva invención de medicamentos y tratamientos a diario. A veces, los investigadores y científicos también encuentran nuevas especies. Su categoría se puede encontrar fácilmente usando el algoritmo de agrupamiento basado en sus similitudes.
• Juegos: también se puede utilizar un algoritmo de agrupación para mostrar los juegos al usuario en función de sus intereses.
• Internet: un usuario navega por muchos sitios web en función de su interés. El historial de navegación se puede agregar para realizar una agrupación en clústeres y, en función de los resultados de la agrupación, se genera el perfil del usuario.

Métodos de agrupamiento

Hay 2 tipos de agrupamiento en programación R: 

• Agrupamiento duro: en este tipo de agrupamiento, el punto de datos pertenece totalmente al clúster o no y el punto de datos se asigna a un solo clúster. El algoritmo utilizado para el agrupamiento duro es el agrupamiento k-means.
• Agrupamiento suave: en el agrupamiento suave, la probabilidad o posibilidad de un punto de datos se asigna en los clústeres en lugar de colocar cada punto de datos en un clúster. Cada punto de datos existe en todos los grupos con alguna probabilidad. El algoritmo utilizado para el agrupamiento suave es el método de agrupamiento difuso o k-means suave.

Agrupación de K-Means en el lenguaje de programación R

K-Means es una técnica iterativa de agrupación dura que utiliza un algoritmo de aprendizaje no supervisado. En esto, el número total de grupos está predefinido por el usuario y, en función de la similitud de cada punto de datos, los puntos de datos se agrupan. Este algoritmo también descubre el centroide del clúster.

Algoritmo: 

• Especifique el número de conglomerados (K): Tomemos un ejemplo de k = 2 y 5 puntos de datos.
• Asigne aleatoriamente cada punto de datos a un grupo: en el siguiente ejemplo, el color rojo y verde muestra 2 grupos con sus respectivos puntos de datos aleatorios asignados.
• Calcular los centroides de los conglomerados: la cruz representa el centroide del conglomerado correspondiente.
• Reasigne cada punto de datos a su centroide de grupo más cercano: el punto de datos verde se asigna al grupo rojo ya que está cerca del centroide del grupo rojo.
• Re-figurar el centroide del clúster

Sintaxis:  kmeans(x, centros, nstart)

dónde,

• x representa array numérica o objeto de marco de datos
• centros representa el valor K o centros de clúster distintos
• nstart representa el número de conjuntos aleatorios que se elegirán

Ejemplo: 

# Library required for fviz_cluster function
install.packages("factoextra")
library(factoextra)
 
# Loading dataset
df <- mtcars
 
# Omitting any NA values
df <- na.omit(df)
 
# Scaling dataset
df <- scale(df)
 
# output to be present as PNG file
png(file = "KMeansExample.png")
 
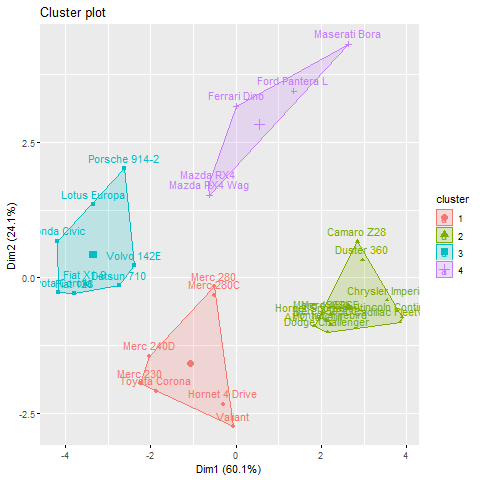
km <- kmeans(df, centers = 4, nstart = 25)
 
# Visualize the clusters
fviz_cluster(km, data = df)
 
# saving the file
dev.off()
 
# output to be present as PNG file
png(file = "KMeansExample2.png")
 
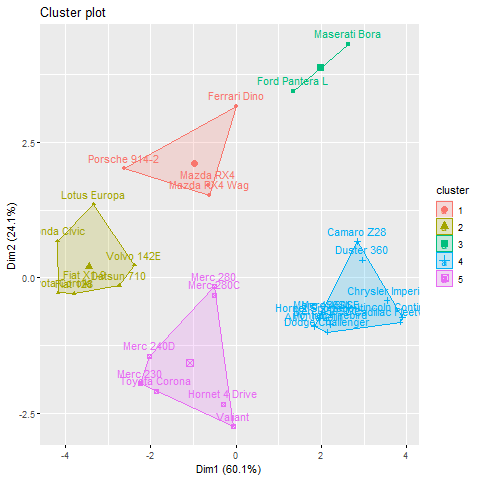
km <- kmeans(df, centers = 5, nstart = 25)
 
# Visualize the clusters
fviz_cluster(km, data = df)
 
# saving the file
dev.off()

Producción: 

When k = 4

When k = 5 

Agrupación por agregación de similitud

La agrupación por agregación de similitud también se conoce como agrupación relacional o método de Condorcet, que compara cada punto de datos con todos los demás puntos de datos en pares. Para un par de valores A y B, estos valores se asignan a los vectores m(A, B) y d(A, B). A y B son iguales en m(A, B) pero diferentes en d(A, B).

donde, S es el grupo

Con la primera condición se construye el clúster y con la siguiente condición se calcula el criterio global de Condorcet. Sigue de manera iterativa hasta que las iteraciones especificadas no se completan o el criterio global de Condorcet no produce ninguna mejora.