Árbol de boas Proto Van Emde | Juego 2 | Construcción

Van Emde Boas Tree admite operaciones de búsqueda, mínimo, máximo, sucesor, predecesor, inserción y eliminación en tiempo O (lglgN), que es más rápido que cualquiera de las estructuras de datos relacionadas, como la cola de prioridad, el árbol de búsqueda binaria, etc. El árbol Proto Van Emde Boas es estructura de datos de tipo de prototipo similar pero no logra la complejidad de O (lglgN). Primero aprenderemos el árbol Proto Van Emde Boas para obtener una comprensión básica del funcionamiento del árbol Van Emde Boas. Aquí N es el tamaño del universo sobre el que se define el árbol.

Nota: Las claves de la estructura de datos de Proto Van Emde Boas deben definirse en un rango de 0 a n (n es un número entero positivo de la forma 2 ^2k ) y funciona cuando no se permiten claves duplicadas.

Abreviaturas: 

1. Proto-VEB es una abreviatura del árbol Proto-Van Emde Boas.
2. Proto-VEB( 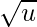) es una abreviatura de Proto-VEB que contiene u número de claves.

Comprensión básica de la estructura del árbol Proto-VEB: 
el árbol de boas Proto Van Emde es una estructura de datos definida recursivamente y se reduce al tamaño de sqrt a medida que subimos en el árbol. Consulte este artículo para comprender los conceptos básicos.

En Proto-VEB usamos una array de bits para representar si una clave está presente o no, ponemos 1 si está presente y 0 en caso contrario.
Aquí, el resumen de un clúster en particular contiene si hay alguna clave presente en un clúster si al menos una clave está presente, entonces el resumen es 1 o 0 en cualquier otro lugar. Los clústeres son segmentos de una array de bits. Un resumen también es una array de bits. Vea la imagen a continuación:

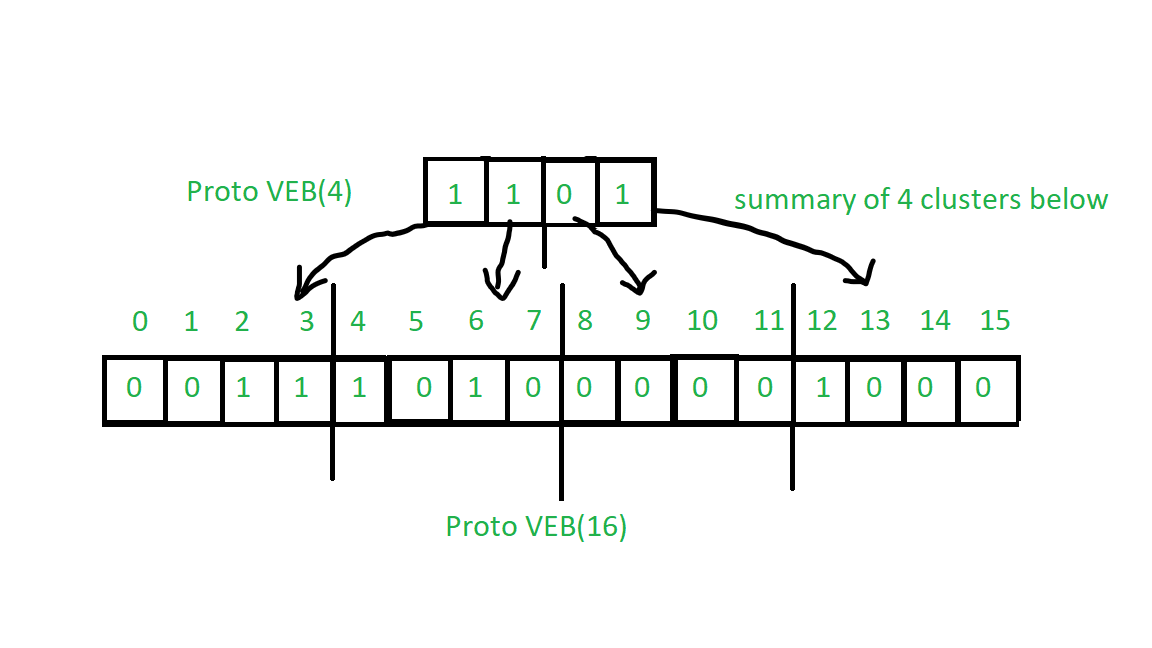
Construcción del árbol Proto VEB:
La imagen de abajo representa la estructura básica de Proto-VEB:

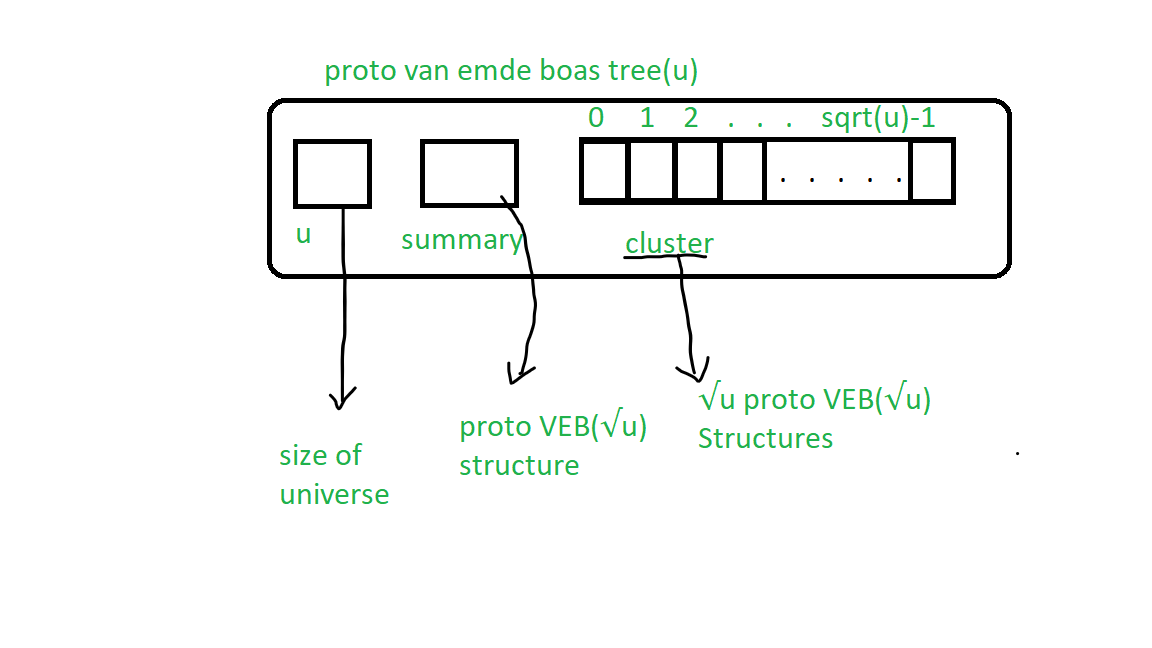
La estructura definida recursivamente tiene dos partes principales:

1. resumen : es un puntero a la estructura Proto-VEB que tiene 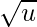 tamaño.
2. clúster: es una array de punteros a estructuras Proto-VEB con 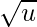 tamaño.

En primer lugar, tenemos que entender algunas funciones y palabras clave: 

• tamaño del universo (u) : Número de claves en la estructura Proto-VEB.
• Alto (x): desde la primera imagen, podemos ver que si queremos llegar al grupo de la clave, podemos dividirlo con  .
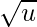  Por ejemplo , queremos saber el grupo de la clave 12 y luego podemos dividirlo por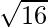  3, por lo que la clave 12 está en el tercer ^grupo .

High(x) = floor( x / )

• low(x): Desde la primera imagen, podemos ver que si queremos la posición de la clave en el clúster, podemos aplicar la operación de módulo x %  .
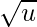  Por ejemplo , si desea encontrar una posición de 7 en el grupo, puede aplicar 7 %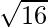  = 3, que es una posición de 7 en el segundo ^grupo .

low(x) = x % )

Procedimiento recursivo de construcción: 

1. Caso base: si el tamaño del universo es 2, entonces es un tamaño base, por lo que no habrá más array de resumen, lo que significa que es nulo y almacenaremos solo una array de bits para 2 claves.
2. Asignaremos recursivamente el resumen como 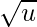 árbol Proto-VEB de tamaño y Proto-VEB de tamaño  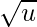a todos los  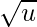grupos. 

Vea la estructura u=4 Proto-VEB en la siguiente imagen:  

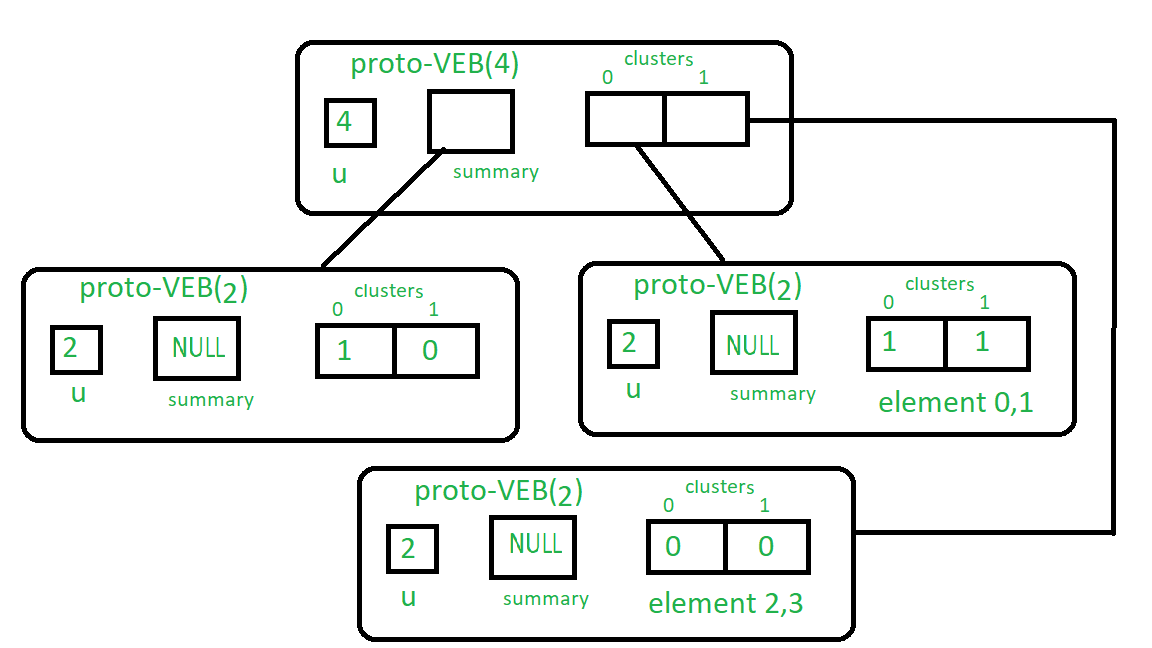
Aquí está el código que representa el algoritmo:

#include <bits/stdc++.h>
using namespace std;
 
class Proto_Van_Emde_Boas {
public:
    // Total number of keys
    int universe_size;
 
    // Summary
    Proto_Van_Emde_Boas* summary;
 
    // Clusters array of Proto-VEB pointers
    vector<Proto_Van_Emde_Boas*> clusters;
 
    int root(int u)
    {
        return (int)sqrt(u);
    }
 
    // Function to return cluster numbers
    // in which key is present
    int high(int x)
    {
        return x / root(universe_size);
    }
 
    // Function to return the position
    // of x in cluster
    int low(int x)
    {
        return x % root(universe_size);
    }
 
    // Function to return index form
    // cluster number and position
    int generate_index(int cluster, int position)
    {
        return cluster * root(universe_size) + position;
    }
 
    // Constructor
    Proto_Van_Emde_Boas(int size)
    {
        universe_size = size;
 
        // Base case
        if (size <= 2) {
 
            // Set summary to nullptr as there is no
            // more summary for size 2
            summary = nullptr;
 
            // Vector of two pointers
            // nullptr in starting
            clusters = vector<Proto_Van_Emde_Boas*>(size, nullptr);
        }
        else {
 
            // Assigning Proto-VEB(sqrt(u)) to summary
            summary = new Proto_Van_Emde_Boas(root(size));
 
            // Creating array of Proto-VEB Tree pointers of size sqrt(u)
            // first all nullptrs are going to assign
            clusters = vector<Proto_Van_Emde_Boas*>(root(size), nullptr);
 
            // Assigning Proto-VEB(sqrt(u)) to all its clusters
            for (int i = 0; i < root(size); i++) {
                clusters[i] = new Proto_Van_Emde_Boas(root(size));
            }
        }
    }
};
 
// Driver code
int main()
{
    Proto_Van_Emde_Boas pveb(4);
}

Complejidad del tiempo: O(sqrt(n))