Cilindro circular recto más grande que se puede inscribir dentro de un cono – Part 1

Dado un cilindro circular recto que está inscrito en un cono de altura h y base de radio r . La tarea es encontrar el mayor volumen posible del cilindro.
Ejemplos: 
 

Input: r = 4, h = 8
Output: 119.087

Input: r = 5, h = 9
Output: 209.333

Enfoque : El volumen de un cilindro es V = πr^2h 
En este problema, primero obtenga una ecuación para el volumen usando triángulos similares en términos de la altura y el radio del cono. Una vez que hayamos modificado la ecuación del volumen, tomaremos la derivada del volumen y resolveremos el valor más grande. 
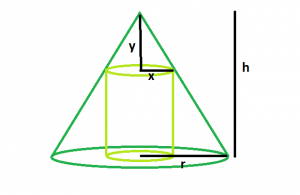
Sea x el radio del cilindro y sea y la distancia desde la parte superior del cono hasta la parte superior del cilindro inscrito. Por lo tanto, la altura del cilindro es h – y 
El volumen del cilindro inscrito es V = πx^2(hy) . 
Usamos el método de razones similares para encontrar una relación entre la altura y el radio, hy y x . 
y/x = h/r 
y = hx/r 
Sustituye la ecuación de y en la ecuación del volumen, V. 
 

V = πx^2(hy) 
V = πx^2(h-hx/r) 
V = πx^2h – πx^3h/r 
ahora, dV/dx = d(πx^2h – πx^3h/r)/ dx 
y configurando dV/dx = 0 
obtenemos, x = 0, 2r/3 
Entonces, x = 2r/3 
y, y = 2h/3 
Entonces, V = π8r^2h/27

A continuación se muestra la implementación del enfoque anterior:
 

// C++ Program to find the biggest
// right circular cylinder that can
// be fit within a right circular cone
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the biggest right circular cylinder
float cyl(float r, float h)
{
 
    // radius and height cannot be negative
    if (r < 0 && h < 0)
        return -1;
 
    // radius of right circular cylinder
    float R = (2 * r) / 3;
 
    // height of right circular cylinder
    float H = (2 * h) / 3;
 
    // volume of right circular cylinder
    float V = 3.14 * pow(R, 2) * H;
 
    return V;
}
 
// Driver code
int main()
{
    float r = 4, h = 8;
    cout << cyl(r, h) << endl;
 
    return 0;
}

// Java Program to find the biggest
// right circular cylinder that can
// be fit within a right circular cone
 
import java.io.*;
 
class GFG {
// Function to find the biggest right circular cylinder
static double cyl(double r, double h)
{
 
    // radius and height cannot be negative
    if (r < 0 && h < 0)
        return -1;
 
    // radius of right circular cylinder
    double R = (2 * r) / 3;
 
    // height of right circular cylinder
    double H = (2 * h) / 3;
 
    // volume of right circular cylinder
    double V = 3.14 * Math.pow(R, 2) * H;
 
    return V;
}
 
// Driver code
     
    public static void main (String[] args) {
     
    double r = 4, h = 8;
    System.out.println (cyl(r, h));
    }
//This code is contributed by ajit
}

# Python 3 Program to find the biggest
# right circular cylinder that can
# be fit within a right circular cone
import math
 
# Function to find the biggest
# right circular cylinder
def cyl(r, h):
 
    # radius and height cannot
    # be negative
    if (r < 0 and h < 0):
        return -1
 
    # radius of right circular cylinder
    R = (2 * r) / 3
 
    # height of right circular cylinder
    H = (2 * h) / 3
     
    # volume of right circular cylinder
    V = 3.14 * math.pow(R, 2) * H
 
    return V
 
# Driver code
r = 4; h = 8;
print(cyl(r, h), "\n")
 
# This code is contributed
# by Akanksha Rai

// C# Program to find the biggest
// right circular cylinder that
// can be fit within a right circular cone
using System;
 
class GFG
{
     
// Function to find the biggest
// right circular cylinder
static double cyl(double r, double h)
{
 
    // radius and height cannot
    // be negative
    if (r < 0 && h < 0)
        return -1;
 
    // radius of right circular cylinder
    double R = (2 * r) / 3;
 
    // height of right circular cylinder
    double H = (2 * h) / 3;
 
    // volume of right circular cylinder
    double V = 3.14 * Math.Pow(R, 2) * H;
 
    return V;
}
 
// Driver code
static public void Main ()
{
    double r = 4, h = 8;
    Console.WriteLine(cyl(r, h));
}
}
 
// This code is contributed by jit_t

<?php
// PHP Program to find the biggest
// right circular cylinder that can
// be fit within a right circular cone
 
// Function to find the biggest
// right circular cylinder
function cyl($r, $h)
{
 
    // radius and height cannot
    // be negative
    if ($r < 0 && $h < 0)
        return -1;
 
    // radius of right circular cylinder
    $R = (int)(2 * $r) / 3;
 
    // height of right circular cylinder
    $H = (int)(2 * $h) / 3;
     
    // volume of right circular cylinder
    $V = 3.14 * pow($R, 2) * $H;
 
    return $V;
}
 
// Driver code
$r = 4;
$h = 8;
echo cyl($r, $h);
 
// This code is contributed by ajit
?>

<script>
// javascript Program to find the biggest
// right circular cylinder that can
// be fit within a right circular cone
 
// Function to find the biggest right circular cylinder
function cyl(r , h)
{
 
    // radius and height cannot be negative
    if (r < 0 && h < 0)
        return -1;
 
    // radius of right circular cylinder
    var R = (2 * r) / 3;
 
    // height of right circular cylinder
    var H = (2 * h) / 3;
 
    // volume of right circular cylinder
    var V = 3.14 * Math.pow(R, 2) * H;
 
    return V;
}
 
// Driver code
     
var r = 4, h = 8;
document.write(cyl(r, h).toFixed(5));
 
// This code is contributed by shikhasingrajput
</script>

119.087

Complejidad de tiempo: O(1)

Espacio Auxiliar: O(1)