HCF (máximo común divisor) o MCD (máximo común divisor) de dos números es el número más grande que divide a ambos.
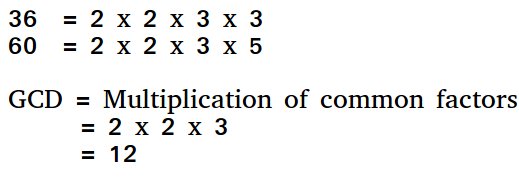
Por ejemplo, GCD de 20 y 28 es 4 y GCD de 98 y 56 es 14.
Una solución simple es encontrar todos los factores primos de ambos números y luego encontrar la intersección de todos los factores presentes en ambos números. Finalmente devuelve el producto de los elementos en la intersección.
Una solución eficiente es utilizar el algoritmo euclidiano, que es el principal algoritmo utilizado para este propósito. La idea es que el MCD de dos números no cambia si se resta un número más pequeño de un número más grande.
C++
// C++ program to find GCD of two numbers
#include <iostream>
using namespace std;
// Recursive function to return gcd of a and b
int gcd(int a, int b)
{
// Everything divides 0
if (a == 0 && b == 0)
return 0;
if (a == 0)
return b;
if (b == 0)
return a;
// base case
if (a == b)
return a;
// a is greater
if (a > b)
return gcd(a - b, b);
return gcd(a, b - a);
}
// Driver program to test above function
int main()
{
int a = 0, b = 56;
cout << "GCD of " << a << " and " << b << " is " << gcd(a, b);
return 0;
}
// This code is contributed by shivanisinghss2110
C
// C program to find GCD of two numbers
#include <stdio.h>
// Recursive function to return gcd of a and b
int gcd(int a, int b)
{
// Everything divides 0
if (a == 0 && b == 0)
return 0;
if (a == 0)
return b;
if (b == 0)
return a;
// base case
if (a == b)
return a;
// a is greater
if (a > b)
return gcd(a - b, b);
return gcd(a, b - a);
}
// Driver program to test above function
int main()
{
int a = 0, b = 56;
printf("GCD of %d and %d is %d ", a, b, gcd(a, b));
return 0;
}
Java
// Java program to find GCD of two numbers
class Test {
// Recursive function to return gcd of a and b
static int gcd(int a, int b)
{
// Everything divides 0
if (a == 0 && b == 0)
return 0;
if (a == 0)
return b;
if (b == 0)
return a;
// base case
if (a == b)
return a;
// a is greater
if (a > b)
return gcd(a - b, b);
return gcd(a, b - a);
}
// Driver method
public static void main(String[] args)
{
int a = 98, b = 56;
System.out.println("GCD of " + a + " and " + b
+ " is " + gcd(a, b));
}
}
Python3
# Recursive function to return gcd of a and b
def gcd(a, b):
# Everything divides 0
if(a == 0 and b == 0):
return 0
if(a == 0):
return b
if(b == 0):
return a
# base case
if(a == b):
return a
# a is greater
if (a > b):
return gcd(a-b, b)
return gcd(a, b-a)
# Driver program to test above function
a = 98
b = 56
if(gcd(a, b)):
print('GCD of', a, 'and', b, 'is', gcd(a, b))
else:
print('not found')
# This code is contributed by Danish Raza
C#
// C# program to find GCD of two
// numbers
using System;
class GFG {
// Recursive function to return
// gcd of a and b
static int gcd(int a, int b)
{
// Everything divides 0
if (a == 0 && b == 0)
return 0;
if (a == 0)
return b;
if (b == 0)
return a;
// base case
if (a == b)
return a;
// a is greater
if (a > b)
return gcd(a - b, b);
return gcd(a, b - a);
}
// Driver method
public static void Main()
{
int a = 98, b = 56;
Console.WriteLine("GCD of " + a + " and " + b
+ " is " + gcd(a, b));
}
}
// This code is contributed by anuj_67.
PHP
<?php
// PHP program to find GCD
// of two numbers
// Recursive function to
// return gcd of a and b
function gcd($a, $b)
{
// Everything divides 0
if($a==0 && $b==0)
return 0 ;
if($a == 0)
return $b;
if($b == 0)
return $a;
// base case
if($a == $b)
return $a ;
// a is greater
if($a > $b)
return gcd( $a-$b , $b ) ;
return gcd( $a , $b-$a ) ;
}
// Driver code
$a = 98 ;
$b = 56 ;
echo "GCD of $a and $b is ", gcd($a , $b) ;
// This code is contributed by Anivesh Tiwari
?>
Javascript
<script>
// Javascript program to find GCD of two numbers
// Recursive function to return gcd of a and b
function gcd(a, b)
{
// Everything divides 0
if (a == 0 && b == 0)
return 0;
if (a == 0)
return b;
if (b == 0)
return a;
// Base case
if (a == b)
return a;
// a is greater
if (a > b)
return gcd(a - b, b);
return gcd(a, b - a);
}
// Driver code
var a = 98, b = 56;
document.write("GCD of " + a + " and " +
b + " is " + gcd(a, b));
// This code is contributed by noob2000
</script>
Producción:
GCD of 98 and 56 is 14
Complejidad de tiempo: O(max(a,b)), donde a y b son los dos enteros dados.
Espacio auxiliar: O(max(a,b)), donde a y b son los dos enteros dados.
Una solución más eficiente es utilizar el operador módulo en el algoritmo euclidiano .
C++
// C++ program to find GCD of two numbers
#include <iostream>
using namespace std;
// Recursive function to return gcd of a and b
int gcd(int a, int b)
{
if (b == 0)
return a;
return gcd(b, a % b);
}
// Driver program to test above function
int main()
{
int a = 98, b = 56;
cout<<"GCD of " <<a << " and "<< b << " is " << gcd(a, b);
return 0;
}
// This code is contributed by shivanisinghss2110
C
// C program to find GCD of two numbers
#include <stdio.h>
// Recursive function to return gcd of a and b
int gcd(int a, int b)
{
if (b == 0)
return a;
return gcd(b, a % b);
}
// Driver program to test above function
int main()
{
int a = 98, b = 56;
printf("GCD of %d and %d is %d ", a, b, gcd(a, b));
return 0;
}
Java
// Java program to find GCD of two numbers
class Test
{
// Recursive function to return gcd of a and b
static int gcd(int a, int b)
{
if (b == 0)
return a;
return gcd(b, a % b);
}
// Driver method
public static void main(String[] args)
{
int a = 98, b = 56;
System.out.println("GCD of " + a +" and " + b +
" is " + gcd(a, b));
}
}
Python3
# Recursive function to return gcd of a and b
def gcd(a,b):
# Everything divides 0
if (b == 0):
return a
return gcd(b, a%b)
# Driver program to test above function
a = 98
b = 56
if(gcd(a, b)):
print('GCD of', a, 'and', b, 'is', gcd(a, b))
else:
print('not found')
# This code is contributed by Danish Raza
C#
// C# program to find GCD of two
// numbers
using System;
class GFG {
// Recursive function to return
// gcd of a and b
static int gcd(int a, int b)
{
if (b == 0)
return a;
return gcd(b, a % b);
}
// Driver method
public static void Main()
{
int a = 98, b = 56;
Console.WriteLine("GCD of "
+ a +" and " + b + " is "
+ gcd(a, b));
}
}
// This code is contributed by anuj_67.
PHP
<?php
// PHP program to find GCD
// of two numbers
// Recursive function to
// return gcd of a and b
function gcd($a, $b)
{
// Everything divides 0
if($b==0)
return $a ;
return gcd( $b , $a % $b ) ;
}
// Driver code
$a = 98 ;
$b = 56 ;
echo "GCD of $a and $b is ", gcd($a , $b) ;
// This code is contributed by Anivesh Tiwari
?>
Javascript
<script>
// Javascript program to find GCD of two numbers
// Recursive function to return gcd of a and b
function gcd(a, b)
{
if (b == 0)
return a;
return gcd(b, a % b);
}
// Driver code
var a = 98, b = 56;
document.write("GCD of " + a +" and " + b +
" is " + gcd(a, b));
// This code is contributed by Ankita saini
</script>
Producción:
GCD of 98 and 56 is 14
Complejidad de tiempo: O(log(max(a,b)), donde a y b son los dos enteros dados.
Espacio auxiliar: O(log(max(a,b)), donde a y b son los dos enteros dados.
Consulte GCD de más de dos (o array) números para encontrar HCF de más de dos números.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por ABHISHEK GAURAV y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA