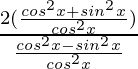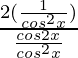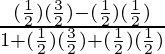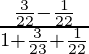Acreditar las siguientes identidades:
Pregunta 16. cos 2 (π/4 – x) – sen 2 (π/4 – x) = sen 2x
Solución:
Resolvamos LHS,
= cos 2 (π/4 – x) – sen 2 (π/4 – x)
Como sabemos que,
cos 2 A – sen 2 A = cos 2 A
Asi que,
= cos 2 (π/4 – x) sen 2 (π/4 – x)
= cos 2 (π/4 – x)
= coseno (π/2 – 2x)
= sen 2x [Como sabemos que, cos (π/2 – A) = sen A]
LHS = RHS
Por lo tanto Probado.
Pregunta 17. cos 4x = 1 – 8 cos 2 x + 8 cos 4 x
Solución:
Resolvamos LHS,
= cos 4x
Como sabemos que,
cos 2x = 2 cos 2 x – 1
Asi que,
cos 4x = 2 cos 2 2x – 1
= 2(2 cos 2 2x – 1) 2 – 1
= 2[(2 cos 2 2x) 2 + 1 2 – 2 × 2 cos 2 x] – 1
= 2(4 cos 4 2x + 1 – 4 cos 2 x) – 1
= 8 cos 4 2x + 2 – 8 cos 2 x – 1
= 8 cos 4 2x + 1 – 8 cos 2 x
LHS = RHS
Por lo tanto Probado.
Pregunta 18. sen 4x = 4 sen x cos 3 x – 4 cos x sen 3 x
Solución:
Resolvamos LHS,
= sen 4x
Como sabemos que,
sen 2x = 2 sen x cos x
cos 2x = cos 2 x – sen 2 x
Asi que,
sen 4x = 2 sen 2x cos 2x
= 2 (2 sen x cos x) (cos 2 x – sen 2 x)
= 4 sen x cos x (cos 2 x – sen 2 x)
= 4 sen x cos 3 x – 4 sen 3 x cos x
LHS = RHS
Por lo tanto probado.
Pregunta 19. 3(sen x – cos x) 4 + 6 (sen x + cos x) 2 + 4 (sen 6 x + cos 6 x) = 13
Solución:
Resolvamos LHS,
= 3(sen x – cos x) 4 + 6 (sen x + cos x) 2 + 4 (sen 6 x + cos 6 x)
Como sabemos que,
(a + b) 2 = a 2 + b 2 + 2ab
(a – b) 2 = a 2 + b 2 – 2ab
a 3 + b 3 = (a+b)(a 2 + b 2 – ab)
Asi que,
= 3{(senx – cosx) 2 } 2 + 6 {(senx) 2 + (cosx) 2 + 2 senx cosx} + 4 {(senx 2 x) 3 + (cos 2 x) 3 }
= 3{(senx) 2 + (cosx) 2 – 2 senx cosx} 2 + 6(sen 2 x + cos 2 x + 2 senx cosx) + 4{(sen 2 x + cos 2 x)(sen 4 x + cos 4 x – sen 2 x cos 2 x)}
= 3(1 – 2 senx cosx) 2 + 6(1 + 2 senx cosx) + 4{(1)(sen 4 x + cos 4 x – seno 2 x cos 2 x)}
Ya que,
sen 2 x + cos 2 x = 1
Asi que,
= 3{1 2 + (2 senx cosx) 2 – 4 senx cosx} + 6(1 + 2 senx cosx) + 4{(senx 2 x) 2 + (cos 2 x) 2 + 2 sen 2 x cos 2 x – 3 sen 2 x cos 2 x}
= 3{1 + 4 sen 2 x cos 2 x – 4 senx cosx} + 6(1 + 2 senx cosx) + 4{(sen 2 x + cos 2 x) 2 – 3 sen 2 x cos 2 x}
= 3 + 12 sen 2 x cos 2 x – 12 senx cosx + 6 + 12 senx cosx + 4{(1) 2 – 3 sen 2 x cos 2 x}
= 9 + 12 sen 2 x cos 2 x + 4(1 – 3 sen 2 x cos 2 x)
= 9 + 12 sen 2 x cos 2 x + 4 – 12 sen 2 x cos 2 x
= 13
LHS = RHS
Por lo tanto probado.
Pregunta 20. 2(sen 6 x + cos 6 x) – 3(sen 4 x + cos 4 x) + 1 = 0
Solución:
Resolvamos LHS,
= 2(sen 6 x + cos 6 x) – 3(sen 4 x + cos 4 x) + 1
Como sabemos que,
(a + b) 2 = a 2 + b 2 + 2ab
a 3 + b 3 = (a + b) (a 2 + b 2 – ab)
Asi que,
= 2(sen 6 x + cos 6 x) – 3(sen 4 x + cos 4 x) + 1
= 2{(sen 2 x) 3 + (cos 2 x) 3 } – 3{(sen 2 x) 2 + (cos 2 x) 2 } + 1
= 2((sen 2 x + cos 2 x)(sen 4 x + cos 4 x – sen 2 x cos 2 x) – 3{(sen 2 x) 2 + (cos 2 x) 2 + 2 sen 2 x cos 2 x – 2 sen 2 x cos 2 x} + 1
= 2{(1)(sen 4 x + cos 4 x + 2 sen 2 x cos 2 x – 3 sen 2 x cos 2 x) – 3((sen 2 x + cos 2 x) 2 – 2 sen 2 x cos 2 x) + 1
Ya que
sen 2 x + cos 2 x = 1
Asi que,
= 2{(sen 2 x + cos 2 x) 2 – 3 sen 2 x cos 2 x} – 3{(1) 2 – 2 sen 2 x cos 2 x} + 1
= 2{(1) 2 – 3 sen 2 x cos 2 x} – 3(1 – 2 sen 2 x cos 2 x) + 1
= 2(1 – 3 sen 2 x cos 2 x) – 3 + 6 sen 2 x cos 2 x + 1
= 2 – 6 sen 2 x cos 2 x – 2 + 6 sen 2 x cos 2 x
= 0
LHS = RHS
Por lo tanto Probado.
Pregunta 21. cos 6 x – sen 6 x = cos 2x (1 – 1/4 sen 2 2x)
Solución:
Resolvamos LHS,
= cos 6 x – sen 6 x
Como sabemos que,
(a + b) 2 = a 2 + b 2 + 2ab
a 3 – b 3 = (a – b) (a 2 + b 2 + ab)
Asi que,
cos 6 x – sen 6 x = (cos 2 x) 3 – (sen 2 x) 3
= (cos 2 x – sen 2 x) (cos 4 x + sen 4 x + cos 2 x sen 2 x)
Como sabemos que,
cos 2x = cos 2 x – sen 2 x
Asi que,
= cos 2x [(cos 2 x) 2 + (sen 2 x) 2 + 2 cos 2 x sen 2 x – cos 2 x sen 2 x]
= cos 2x [(cos 2 x) 2 + (sen 2 x) 2 – 1/4 × 4 cos 2 x sen 2 x]
Como sabemos que,
sen 2 x + cos 2 x = 1
Asi que,
= cos2x [(1) 2 – 1/4 × (2 cosx senx) 2 ]
Como sabemos que,
sen2x = 2 senx cosx
Asi que,
= cos 2x [1 – 1/4 × (sen 2x) 2 ]
= cos 2x [1 – 1/4 × sen 2 2x]
LHS = RHS
Por lo tanto probado.
Pregunta 22. tan (π/4 + x) + tan (π/4 – x) = 2 seg2x
Solución:
Resolvamos LHS,
= bronceado (π/4 + x) + bronceado (π/4 – x)
Como sabemos que,
tan (A + B) = (tan A + tan B)/(1 – tan A tan B)
tan (A – B) = (tan A – tan B)/(1 + tan A tan B)
Asi que,
=
Ya que, tan π/4 = 1
Asi que,
=
=
Usando fórmulas, obtenemos
(a – b)(a + b) = a 2 – b 2
(a + b) 2 = a 2 + b 2 + 2ab & (a – b) 2 = a 2 + b 2 – 2ab
Asi que,
=
=
=
Como sabemos que,
tan x = sen x/cos x
Asi que,
=
=
=
Usando las fórmulas, obtenemos
cos 2 x + sen 2 x = 1 & cos 2x = cos 2 x – sen 2 x
Asi que,
=
= 2/cos2x
= 2 seg2x
LHS = RHS
Por lo tanto Probado.
Pregunta 23. cot 2 x – tan 2 x = 4cot2x cosec2x
Solución:
Resolvamos LHS,
= cuna 2 x – bronceado 2 x
= cos 2 x/sen 2 x – sen 2 x/cos 2 x
= [(cos 2 x) 2 – (sen 2 x) 2 ] / sen 2 x cos 2 x
= [(cos 2 x + sen 2 x)(cos 2 x – sen 2 x)] / sen 2 x cos 2 x
= (1 × cos2x) / sen 2 x cos 2 x
= 4cos2x / 4sen 2 xcos 2 x
= 4(cos2x) / (sen2x) 2
= 4(cos2x) / (sen2x) × 1 / (sen2x)
= 4 cot2x cosex2x
LHS = RHS
Por lo tanto probado
Pregunta 24. cos4x – cos4α = 8(cosx – cosα)(cosx + cosα)(cosx – sinα)(cosx + sinα)
Solución:
Resolvamos RHS,
= 8(cosx – cosα)(cosx + cosα)(cosx – sinα)(cosx + sinα)
= 8(cos 2 x – cos 2 α)(cos 2 x – sen 2 α)
= 8(cos 4 x – cos 2 x × sen 2 α – cos 2 α × cos 2 x + cos 2 α × sen 2 α)
= 8{cos 4 x – cos 2 x (sen 2 α + cos 2 α) + cos 2 α × sen 2 α}
= 8{cos 4 x – cos 2 x + cos 2 α × (1 – cos 2 α)}
= 8{cos 4 x – cos 2 x + cos 2 α – cos 4 α)}
= 8{cos 2 x (cos 2 x – 1) + cos 2 α × (1 – cos 2 α)}
= 8{1/2 cos 2 x (2 cos 2 x – 1 – 1) – 1/2 cos 2 α (2 cos 2 α – 1 -1)}
= 8{1/2 cos 2 x (cos2x – 1) – 1/2 cos 2 α (cos 2 α – 1)}
= 8[1/4 {2cos 2 x (cos2x – 1) – 2cos 2 x (cos2α – 1)}]
= 8[1/4 {(1 + cos2x)(cos2x – 1) – (1 + cos2α)(cos2α – 1)}]
= 8[1/4 { cos 2 2x – 1 – cos 2 2α + 1}]
= 8[1/8 {2cos 2 2x – 2cos 2 2α}]
= [{(1 + cos4x) – (1 + cos4α)}]
= [1 + cos4x – 1 – cos4α]
= cos4x – cos4α
LHS = RHS
Por lo tanto probado
Pregunta 25. sen3x + sen2x – senx = 4 senx cos(x/2) cos(3x/2)
Solución:
Resolvamos LHS,
= sen3x + sen2x – senx
= sin3x + 2sin(2x – x)/2 cos(2x + x)/2
= sen3x + 2sen(x/2) cos(3x/2)
= 2sen(3x/2) cos(3x/2) + 2sen(3x/2) cos(x/2)
= 2 cos(3x/2)[sen(3x/2) cos(x/2)]
= 2 cos(3x/2)[2sen(3x/2+x/2)/2 cos(3x/2 – x/2)/2]
= 2 cos(3x/2)[2senx cos(x/2)]
= 4 senx cos(x/2) cos(3x/2)
LHS = RHS
Por lo tanto probado.
Pregunta 26.  = (√3 + √2)(√2 + 1) = √2 + √3 + √4 + √6
= (√3 + √2)(√2 + 1) = √2 + √3 + √4 + √6
Solución:
Resolvamos LHS,
tan(82,5)° = tan(90 – 7,5)° = cot(7,5)° = 1/ tan(7,5)°
Tenemos,
tan(x/2) = senx/(1 + cosx)
Ahora al poner x = 15°, obtenemos
tan(15/2) = sen15°/(1 + cos15°)
= sen(45-30)°/{1 + coseno(45-30)°}
= (sen45°cos30° – sen30°cos45°) / (1 + cos45° sen30°)
=
=
=
Ahora,
tan(82.5)° = 1/tan(7.5)°
= (2√2 + √3 + 1)/(√3 – 1)
= (2√2 + √3 + 1)/(√3 – 1) × (√3 + 1)/(√3 + 1)
= [√3 + 1(2√2 + √3 + 1)] / [(√3) 2 – 1 2 ]
= (2√6 + 3 + √3 + 2√2 + √3 + 1) / (3 – 1)
= (2√6 + 2√3 + 2√2 + 4) / (2)
= √6 + √3 + √2 + 2
= √2 + √3 + √4 + √6 …..(yo)
= √6 + √3 + 2 + √2
= √3(√2 + 1) + √2(√2 + 1)
= (√3 + √2)(√2 + 1) …..(ii)
De la ecuación (i) y (ii), obtenemos
tan(82.5)° = (√3 + √2)(√2 + 1) = √2 + √3 + √4 + √6
LHS = RHS
Por lo tanto probado
Pregunta 27. 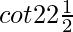 = √2 + 1
= √2 + 1
Solución:
Como sabemos que, π/8 =
= 45°
Sea A =
Usando la identidad cot2A = (cot 2 A – 1)/2cotA, obtenemos
cuna45° = {cot 2 (
)° – 1} / 2cot(
)°
⇒ 1 = {cot 2 (
)° – 1} / 2cot(
)°
⇒ 2cot(
)° – cuna 2 (
)° + 1 = 0
⇒ cuna 2 (
)° – 2 cuna (
)° – 1 = 0
⇒ { cuna 2 (
) – 2 cuna (
)° + 1} – 2 = 0
⇒ { cuna(
)° – 1} 2 = 2
⇒ cuna(
)° – 1 = √2
⇒ cuna(
)° = √2 + 1
LHS = RHS
Por lo tanto probado
Pregunta 28 (i). Si cosx = (-3/5) y x está en el tercer cuadrante, encuentra los valores de cos(x/2), sen(x/2), sen2x.
Solución:
Dado que,
cos x = (-3/5)
⇒ cosx = cos 2 (x/2) – sen 2 (x/2)
⇒ -3/5 = 2 cos 2 (x/2) – 1
⇒ 1 – 3/5 = 2 cos 2 (x/2)
⇒ 2/5 = 2 cos 2 (x/2)
⇒ 1/5 = cos 2 (x/2)
⇒ cos(x/2) = ± √(1/5)
Además, dado que x se encuentra en el tercer cuadrante, entonces x/2 se encuentra en el segundo cuadrante.
cos(x/2) = – √(1/5)
Otra vez,
cosx = cos 2 (x/2) – sen 2 (x/2)
⇒ -3/5 = (- √(1/5)) 2 – sen 2 (x/2)
⇒ – 3/5 = 1/5 – sen 2 (x/2)
⇒ -1/5 -3/5 = -sen 2 (x/2)
⇒ 4/5 = sen 2 (x/2)
⇒ sen(x/2) = ± 2/√5
Está dado que x está en el 3er cuadrante, entonces x/2 está en el 2do cuadrante.
sen(x/2) = 2/√5
Ahora,
senx = √(1 – cos 2 x)
= √(1 – (-3/5)) 2
= √(1 – 9/25)
= ± 4/5
Se da x llies en el 3er cuadrante, por lo que senx es negativo.
senx = – 4/5
sen2x = 2 senx cosx
= 2 (-4/5) (-3/5)
= 24/25
Por lo tanto, el valor de cos(x/2) = – √(1/5), sin(x/2) = 2/√5 y sin2x = 24/25.
Pregunta 28 (ii). Si cosx = (-3/5) y x está en el 3er cuadrante, encuentra los valores de sin2x y sin(x/2).
Solución:
Dado que,
cos x = (-3/5)
senx =
⇒ senx = ± 4/5
Aquí, x se encuentra en el segundo cuadrante
Entonces, senx = 4/5
Como sabemos que,
sen2x = 2 senx cosx
sen2x = 2 × 4/5 × (-3/5) = (-24/25)
Ahora,
cosx = 1 – 2 sen 2 (x/2)
⇒ 2sen2(x/2) = 1 – (-3/5) = 8/5
⇒ senx2(x/2) = 4/5
⇒ sen(x/2) = ± 2/√5
Como x está en el segundo cuadrante,
x/2 se encuentra en el primer cuadrante
Entonces, sin(x/2) = 2/√5
Por tanto, el valor de sin2x = (-24/25) y sin(x/2) = 2/√5
Pregunta 29. Si senx = √5/3 y x está en el 2.º cuadrante, encuentra los valores de cos(x/2), sen(x/2) y tan(x/2).
Solución:
Dado que, senx = √5/3
Como sabemos que senx = P/H
Entonces, P = √5, H = 3 y B = 2
Ahora, cosx = B/H = -2/3
Asi que,
cos(x/2) = √{(1 + cosx)/2} = √{(1 – 2/3)/2} = 1/√6
sin(x/2) = √{(1 – cosx)/2} = √{(1 + 2/3)/2} = √(5/6)
tan(x/2) = sin(x/2)/cos(x/2) = {√(5/6)} / (1/√6) = √5
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA