El problema del horizonte | conjunto 2

Dados n edificios rectangulares en una ciudad bidimensional, calcula el horizonte de estos edificios, eliminando las líneas ocultas. La tarea principal es ver los edificios desde un lado y eliminar todas las secciones que no son visibles. 

Todos los edificios comparten un fondo común y cada edificio está representado por un triplete (izquierda, altura, derecha) 

• izquierda: es x coordenada en el lado izquierdo (o pared).
• right: es la coordenada x del lado derecho.
• ht: es la altura del edificio.

Un horizonte es una colección de tiras rectangulares. Una franja rectangular se representa como un par (izquierda, altura) donde izquierda es la coordenada x del lado izquierdo de la franja y ht es la altura de la franja.

Ejemplos: 

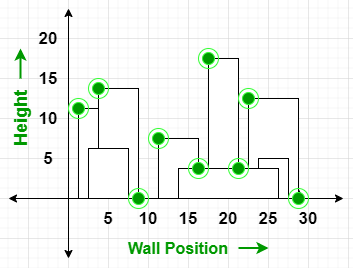
Entrada: edificios[][] = { {1, 11, 5}, {2, 6, 7}, {3, 13, 9}, {12, 7, 16}, {14, 3, 25}, { 19, 18, 22}, {23, 13, 29}, {24, 4, 28} }
Salida: { {1, 11}, {3, 13}, {9, 0}, {12, 7}, {16, 3}, {19, 18}, {22, 3}, {23, 13}, {29, 0} }
Explicación:
el horizonte se forma en función de los puntos clave (representados por puntos «verdes») 
eliminando paredes ocultas de los edificios.
 

Entrada: edificios[ ][ ] = { {1, 11, 5} }
Salida: { {1, 11}, {5, 0} }

Acercarse: 

1. De los tripletes proporcionados para cada edificio, recupere la ubicación del muro izquierdo, la altura y el valor de ubicación del muro derecho.
2. Guarde la pared izquierda con su valor negativo de altura y la pared derecha con su altura real como un par en paredes vectoriales . Esto se hace para distinguir entre las paredes izquierda y derecha del mismo edificio.
3. Ordena las paredes en orden ascendente.
4. Atraviese las paredes vectoriales , si se encuentra una pared izquierda, almacene la altura de la pared izquierda en el conjunto múltiple M. De lo contrario, si encuentra una pared derecha, elimine su altura correspondiente del conjunto múltiple .
5. Compruebe si el valor superior ha cambiado o no. Si ha cambiado, actualice el valor superior y almacene el valor de abscisa (coordenada x) del muro actual y el valor superior actualizado en un vector como horizonte .
6. Imprime los pares de valores almacenados en el vector del horizonte.

A continuación se muestra la implementación de 

el enfoque anterior: 

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to create skyline
vector<pair<int, int> >
createSkyline(vector<vector<int> >& buildings)
{
 
    // Get the number of buildings
    int N = buildings.size();
 
    // To store the left and right
    // wall position of the buildings
    vector<pair<int, int> > wall;
 
    // Triplet of building structure
    // parameters
    int left, height, right;
    for (int i = 0; i < N; i++) {
 
        // Get left point of building
        left = buildings[i][0];
 
        // Get height of building
        height = buildings[i][1];
 
        // Get right point of building
        right = buildings[i][2];
 
        // Store left point and height
        // of the left wall
 
        // Negative value means left wall
        // will be inserted to multiset first
        // for the same abscissa(x) as right wall
        wall.push_back({ left, -height });
 
        // Store right point and height
        // of the right wall
        wall.push_back(
            make_pair(right, height));
    }
 
    // Sort the walls in ascending order
    sort(wall.begin(), wall.end());
 
    // To store skyline: output
    vector<pair<int, int> > skyline;
 
    // Initialize a multiset to
    // keep left wall heights sorted
    multiset<int> leftWallHeight = { 0 };
 
    // Current max height among
    // leftWallHeights
    int top = 0;
 
    // Traverse through the sorted walls
    for (auto w : wall) {
 
        // If left wall is found
        if (w.second < 0) {
 
            // Insert the height
            leftWallHeight.insert(-w.second);
        }
 
        // If right wall is found
        else {
 
            // Remove the height
            leftWallHeight.erase(
                leftWallHeight.find(w.second));
        }
 
        // Mark a skyline point if top changes
        // .rbegin(): reverse iterator
        if (*leftWallHeight.rbegin() != top) {
 
            top = *leftWallHeight.rbegin();
            skyline.push_back(
                make_pair(w.first, top));
        }
    }
 
    // Return skyline to printSkyline
    return skyline;
}
 
// Function to print the output skyline
void printSkyline(
    vector<vector<int> >& buildings)
{
 
    // Function call for creating skyline
    vector<pair<int, int> > skyline
        = createSkyline(buildings);
 
    cout << "Skyline for given"
         << " buildings:\n{";
 
    for (auto it : skyline) {
 
        cout << "{" << it.first << ", "
             << it.second << "} ";
    }
    cout << "}";
}
 
// Driver Code
int main()
{
    vector<vector<int> > buildings;
 
    // Given left and right location
    // and height of the wall
    buildings = { { 1, 11, 5 }, { 2, 6, 7 },
                  { 3, 13, 9 }, { 12, 7, 16 },
                  { 14, 3, 25 }, { 19, 18, 22 },
                  { 23, 13, 29 }, { 24, 4, 28 } };
 
    // Function Call
    printSkyline(buildings);
    return 0;
}

Otro enfoque:

import heapq
def getSkyline(buildings):
      # Stores the building information in the following manner:[left,right,height]
    buildings=list(map(lambda x: [x[0],x[2],x[1]],buildings))
     
    buildings_start=[0] # priority queue
    buildings_end=dict() #map
     
    # Stores the position and height of the present building and whether it is the endpoint of a building
    new_buildings=[]
    for s,e,h in buildings:
        new_buildings.append((s,h,False))
        new_buildings.append((e,h,True))
         
    # Sorting the buildings according to their position
    new_buildings.sort(key= lambda x:(x[0],x[2]))
     
    # Stores the answer
    skyline=[]
    for x,y,end in new_buildings:           
        if not end:
        # if it is the starting point of a building push it in the heap
            if (not skyline) or y>skyline[-1][1]:
                if skyline and x==skyline[-1][0]:
                    skyline[-1][1]=y
                else:
                    skyline.append([x,y])
                heapq.heappush(buildings_start,-y)
            else:
                heapq.heappush(buildings_start,-y)
        else:
        # if it is the ending point of a building
            if y==skyline[-1][1]:
                heapq.heappop(buildings_start)
                if x==skyline[-1][0]:
                    skyline.pop()
                y=heapq.heappop(buildings_start)
                while -y in buildings_end:
                    buildings_end[-y]-=1
                    if buildings_end[-y]==0:
                        del(buildings_end[-y])
                    y=heapq.heappop(buildings_start)
                if -y!=skyline[-1][1]:
                    skyline.append([x,-y])
                heapq.heappush(buildings_start,y)
            else:
                buildings_end[y]=buildings_end.get(y,0)+1
    return skyline
 
if __name__ == '__main__':
    buildings = [ [ 1, 11, 5 ], [ 2, 6, 7 ],
                  [ 3, 13, 9 ], [ 12, 7, 16 ],
                  [ 14, 3, 25 ], [ 19, 18, 22 ],
                  [ 23, 13, 29 ], [ 24, 4, 28 ] ]
    print(getSkyline(buildings))

Complejidad de tiempo: O(N * log(N))  
Espacio auxiliar: O(N)