Procesamiento de Señales y Series Temporales (Análisis de Datos)

El procesamiento de señales es un campo de la ingeniería que se enfoca en analizar señales analógicas y digitales con respecto al tiempo. El análisis de series temporales es una de las categorías del procesamiento de señales.

Una serie temporal es una secuencia de puntos de datos registrados a intervalos regulares de tiempo. El análisis de series de tiempo es un paso importante antes de desarrollar un pronóstico de la serie, y el orden de los valores es importante en el análisis de series de tiempo. Este proceso ayuda a extraer estadísticas significativas y otras características de los datos que ayudan a crear un pronóstico preciso. Las series de tiempo se utilizan ampliamente para datos como el clima, el precio de las acciones, las ventas minoristas, etc.

Cubriremos los siguientes temas en esta sección:

1. Moving Average
2. Autoregressive Models
3. ARMA Models 

Estos se explican a continuación a continuación.

1. Promedio móvil:
un promedio móvil (MA) es un cálculo ampliamente utilizado para analizar series de tiempo. Esto especifica una ventana de datos para un período de tiempo particular que se promedia cada vez por un período cuando hay nuevos datos disponibles.

Los dos promedios móviles comúnmente utilizados son:

1. Promedio móvil simple (SMA):
   el cálculo de SMA proporciona los datos promedio para un número definido de períodos de tiempo. La fórmula matemática de la siguiente manera: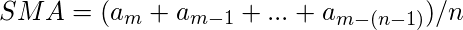

   
   Donde,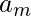
   = parámetro del modelo
   n = total de días

2. Promedio móvil exponencial (EMA):
   el promedio móvil exponencial da más prioridad a los datos recientes. La fórmula matemática de la siguiente manera: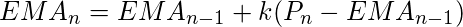

   
   Donde,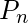
   = precio de cierre actual
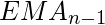   = periodos anteriores EMA [SMA para el primer cálculo]
   k = 2 / (N+1) [constante exponencial o suavizante]
   N = Número total de días considerados para el cálculo de EMA

Cálculo de EMA:
Aquí calculamos EMA para 5 días. Normalmente, para el primer caso, tomamos el precio de cierre actual o el valor de SMA de los 5 días anteriores para obtener el primer EMA. Para el siguiente ejemplo, el precio de cierre actual ($22,81) se toma como el primer valor de EMA.

El siguiente paso es calcular el valor de k. Dado que el cálculo se basa en 5 días, N = 5 y el valor de k se calcula de la siguiente manera:

 k = 2/(5+1) = 0.3 

DÍA	PRECIO DE CIERRE	EMA	SMA
1	22.81	22.81	–
2	23.09	–	–

La EMA para el segundo día se calcula de la siguiente manera:

Current closing price = 23.09
Previous period EMA = 22.81
k = 0.3 

EMA 
= 22.81 + 0.3 * (23.09 - 22.81)
= 22.81 + 0.3 * 0.28
= 22.81 + 0.084
= 22.894 

DÍA	PRECIO DE CIERRE	EMA	SMA
1	22.81	22.81	–
2	23.09	22.89	–
3	22.91	–	–

La EMA para el tercer día se calcula de la siguiente manera:

Current closing price = 22.91
Previous period EMA = 22.89
k = 0.3 

EMA 
= 22.89 + 0.3 * (22.91 - 22.89)
= 22.89 + 0.3 * .02
= 22.89 + .006
= 22.896 

DÍA	PRECIO DE CIERRE	EMA	SMA
1	22.81	22.81	–
2	23.09	22.89	–
3	22.91	22.89	–

Cálculo de SMA:
dado que consideramos el total de días (N) como 5, el SMA se calcula como el promedio de los 5 últimos precios de cierre.

DÍA	PRECIO DE CIERRE	EMA	SMA
1	22.81	22.81	–
2	23.09	22.89	–
3	22.91	22.89	–
4	23.23	22.99	–
5	22.83	22.94	–

La SMA para 5 días se calcula de la siguiente manera:

SMA 
= (22.81 + 23.09 + 22.91 + 23.23 + 22.83) / 5
= 114.87 / 5 
= 22.97  

DÍA	PRECIO DE CIERRE	EMA	SMA
1	22.81	22.81	–
2	23.09	22.89	–
3	22.91	22.89	–
4	23.23	22.99	–
5	22.83	22.94	22.97
6	23.05	–	–

2. Modelos autorregresivos:
se puede usar un modelo autorregresivo para predecir datos futuros basados ​​en datos pasados. En este modelo, se supone que los datos dependen de sus datos anteriores. Dado que los modelos autorregresivos dependen totalmente de datos pasados ​​para generar modelos futuros, existen posibilidades de generar datos inexactos en determinadas condiciones, como crisis financieras o cambios tecnológicos repentinos.
La fórmula matemática de la siguiente manera:

Cálculo AR:
Los siguientes datos proporcionan el precio de las acciones de hoy (t), un día antes (t-1), dos días antes (t-2) y tres días antes (t-3).

t	t-1	t-2	t-3
23.23	22.91	23.09	22.81
22.83	23.23	22.91	23.09
23.05	22.83	23.23	22.91
23.02	23.05	22.83	23.23
23.29	23.02	23.05	22.83
23.41	23.29	23.02	23.05
23.49	23.41	23.29	23.02
24.6	23.49	23.41	23.29
24.63	24.6	23.49	23.41
24.51	24.63	24.6	23.49
23.73	24.51	24.63	24.6
23.31	23.73	24.51	24.63
23.53	23.31	23.73	24.51
23.06	23.53	23.31	23.73
23.25	23.06	23.53	23.31
23.12	23.25	23.06	23.53
22.8	23.12	23.25	23.06
22.84	22.8	23.12	23.25

Con los datos del precio de las acciones anteriores, debe realizar la regresión lineal para obtener los parámetros necesarios para el modelo AR. Para esto, puede usar la función de análisis de datos de Excel. Para la regresión, puede proporcionar datos t como entrada Y y (t-1), (t-2), (t-3) como entrada X. Microsoft Excel le proporcionará el siguiente resultado.

Estadísticas de regresión:

Multiple R: 0.786903932
R Square: 0.619217798
Adjusted R Square: 0.537621612
Standard Error: 0.398415364
Observations: 18 

Coeficientes	Error estándar
Interceptar	8.59250239	4.494566177
t-1	0.840795074	0.249566271
t-2	0.100511124	0.331626753
t-3	-0.308260596	0.250400704

Veamos cómo usar los valores de salida de la regresión.

Datos de existencias anteriores:

Coefficient of t-1 = 0.840795074 and Close price = 22.8
Coefficient of t-2 = 0.100511124 and Close price = 23.12
Coefficient of t-3 = -0.308260596 and Close price = 23.25 

Valor de constante:

Coefficient of Intercept = 8.59250239 = 8.6 

Error estándar:

t-1 = 0.249566271
t-2 = 0.331626753
t-3 = -0.250400704 

Standard Error 
= 0.25 + 0.33 - 0.25
= 0.33 

AR 
= 8.6 + [ (0.84*22.8) + (0.1*23.12) + (-0.31*23.25) ] + 0.33
= 8.6 + [ 19.15 + 2.31 - 7.20] + 0.33
= 8.6 + 14.26 + 0.33
= 23.19 

En lugar de realizar todo el cálculo, puede predecir el precio de las acciones de mañana con el precio de las acciones de hoy y el valor R cuadrado (consulte la salida de estadísticas de regresión anterior).

Suponga que el precio de las acciones de hoy es de $22.84, entonces el precio de las acciones de mañana se calcula como:

AR(t+1) = Coefficient of Intercept + (R square * Today's Price) 
                                        + Standard Error

R Square = 0.619217798 

Standard Error (from regression statistics) = 0.398415364 

AR 
= 8.6 + (0.619*22.84) + 0.39
= 8.6 + 14.14 + 0.39
= 23.13 

3. Modelos
ARMA: el modelo ARMA es otra herramienta utilizada para pronosticar una serie de tiempo. Estos modelos se basan en la combinación de modelos autorregresivos y de promedio móvil. En el modelo AR, usamos datos pasados ​​para hacer una regresión de la variable y en el modelo MA, usamos la suma de la media de la serie de tiempo para un pronóstico.

Dado que el modelo ARMA es la combinación de la parte AR y la parte MA, este modelo se denomina modelo ARMA(p, q), donde p es la parte AR yq es la parte MA.

La fórmula matemática es la siguiente:

Donde,
= parámetro del modelo autorregresivo
= parámetro del modelo de promedio móvil
c = una constante
= término de error [Ruido blanco]