Dado un entero positivo ![]() . La tarea es representarlo como una suma del máximo número posible de números primos. (N > 1)
. La tarea es representarlo como una suma del máximo número posible de números primos. (N > 1)
Ejemplos :
Input : N = 5 Output : 2 3 Input : N = 6 Output : 2 2 2
Al principio, podría parecer que el problema involucra algún uso de la conjetura de Goldbach . Pero la observación clave aquí es maximizar la cantidad de términos utilizados, debe usar números tan pequeños como sea posible. Esto lleva a la siguiente idea:
- Si N es par, se puede representar como una suma de
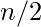 dos.
dos. - De lo contrario,
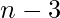 tiene que ser par y, por lo tanto, N puede representarse como la suma de uno 3 y
tiene que ser par y, por lo tanto, N puede representarse como la suma de uno 3 y 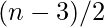 dos.
dos.
Este es el número máximo de primos cuya suma es N.
A continuación se muestra la implementación del enfoque anterior:
C++
// CPP program to represent a number as a
// sum of maximum possible number of
// Prime Numbers
#include <bits/stdc++.h>
using namespace std;
// Function to represent a number as a
// sum of the maximum possible number
// of Prime Numbers
void printAsMaximalPrimeSum(int n)
{
// If n is odd, print one 3
if (n % 2 == 1) {
cout << "3 ";
n -= 3;
}
// Now n is even, print 2 n/2 times
while (n) {
cout << "2 ";
n -= 2;
}
}
// Driver Code
int main()
{
int n = 5;
printAsMaximalPrimeSum(n);
}
Java
// Java program to represent a number as a
// sum of maximum possible number of
// Prime Numbers
import java.io.*;
class GFG {
// Function to represent a number as a
// sum of the maximum possible number
// of Prime Numbers
static void printAsMaximalPrimeSum(int n)
{
// If n is odd, print one 3
if (n % 2 == 1) {
System.out.print( "3 ");
n -= 3;
}
// Now n is even, print 2 n/2 times
while (n>0) {
System.out.print( "2 ");
n -= 2;
}
}
// Driver Code
public static void main (String[] args) {
int n = 5;
printAsMaximalPrimeSum(n);
}
}
// This Code is contributed by inder_verma..
Python3
# Python3 program to represent a number as a
# sum of maximum possible number of
# Prime Numbers
# Function to represent a number as a
# sum of the maximum possible number
# of Prime Numbers
def printAsMaximalPrimeSum( n):
# If n is odd, print one 3
if ( n % 2 == 1):
print("3 ",end="")
n -= 3
# Now n is even, print 2 n/2 times
while ( n>0):
print("2 ",end="")
n -= 2
# Driver Code
n = 5
printAsMaximalPrimeSum( n)
# This code is contributed by ihritik
C#
// C# program to represent a number as a
// sum of maximum possible number of
// Prime Numbers
using System;
class GFG
{
// Function to represent a number as a
// sum of the maximum possible number
// of Prime Numbers
static void printAsMaximalPrimeSum(int n)
{
// If n is odd, print one 3
if (n % 2 == 1) {
Console.Write("3 ");
n -= 3;
}
// Now n is even, print 2 n/2 times
while (n>0) {
Console.Write("2 ");
n -= 2;
}
}
// Driver Code
public static void Main()
{
int n = 5;
printAsMaximalPrimeSum(n);
}
}
// This code is contributed by ihritik
PHP
<?php
// PHP program to represent a number as a
// sum of maximum possible number of
// Prime Numbers
// Function to represent a number as a
// sum of the maximum possible number
// of Prime Numbers
function printAsMaximalPrimeSum($n)
{
// If n is odd, print one 3
if ($n % 2 == 1) {
echo "3 ";
$n -= 3;
}
// Now n is even, print 2 n/2 times
while ($n>0) {
echo "2 ";
$n -= 2;
}
}
// Driver Code
$n = 5;
printAsMaximalPrimeSum($n);
// This code is contributed by ihritik
?>
Javascript
<script>
// Javascript program to represent a number as a
// sum of maximum possible number of
// Prime Number
// Function to represent a number as a
// sum of the maximum possible number
// of Prime Numbers
function printAsMaximalPrimeSum(n)
{
// If n is odd, print one 3
if (n % 2 == 1) {
document.write( "3 ");
n -= 3;
}
// Now n is even, print 2 n/2 times
while (n>0) {
document.write( "2 ");
n -= 2;
}
}
// driver program
let n = 5;
printAsMaximalPrimeSum(n);
</script>
Producción:
3 2
Complejidad de tiempo: O(N)
Publicación traducida automáticamente
Artículo escrito por Abdullah Aslam y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA