Hay 6 personas sentadas en una mesa redonda en la que dos personas tienen el mismo nombre. ¿Cuál es la probabilidad de que los dos individuos del mismo nombre sean vecinos?
Solución (Método 1): ¡ El número total de formas en que 6 personas pueden sentarse en una mesa redonda es (6-1)! = 5! = 120 .
¡Si consideramos a dos personas con el mismo nombre como una persona, hay 5 personas que pueden sentarse (5-1)! maneras y estos individuos se pueden sentar juntos en 2! maneras.
Entonces, probabilidad requerida =(2*(5-1)!)/(6-1)!= 2/5 .
Entonces, la respuesta es 2/5 = 0.4 .
Solución (Método 2): Fijamos a uno del mismo nombre en cualquier posición. Ahora nos quedan 5 lugares de los cuales 2 se pueden sentar vecinos.
Por lo tanto, la respuesta es 2/5 = 0,4 .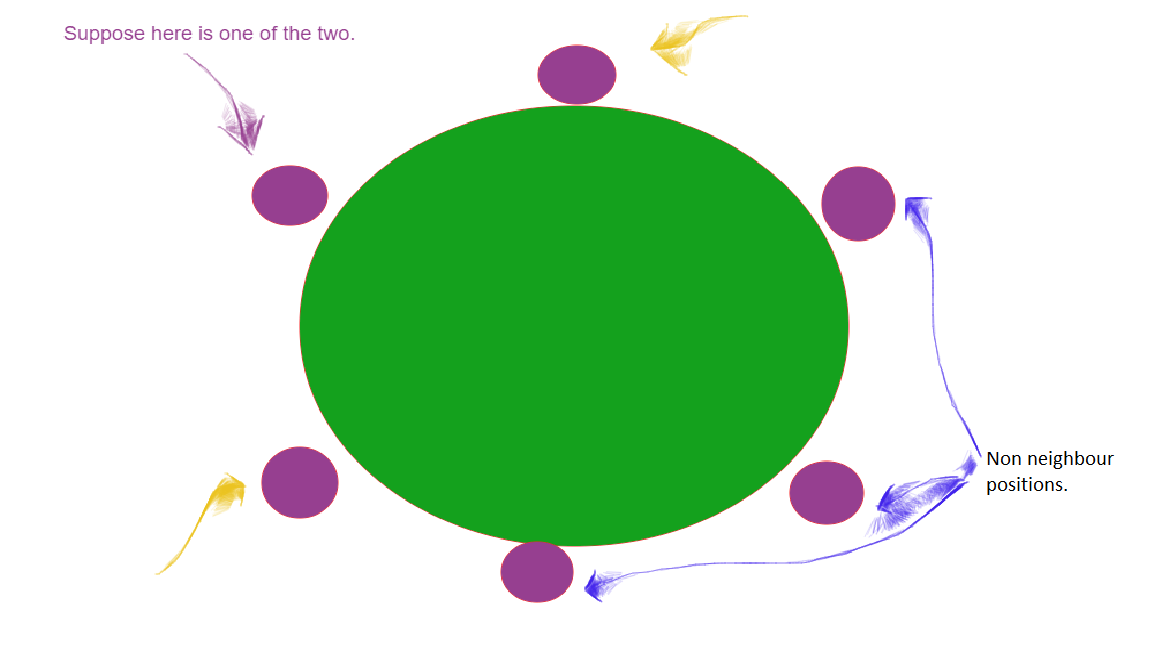
Publicación traducida automáticamente
Artículo escrito por PLACEMENT__CHAHIYE y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA