Máquina de vectores de soporte dual

Requisito previo: separación de hiperplanos en SVM

La ecuación del multiplicador de Lagrange para la máquina de vectores de soporte. La ecuación de eso puede estar dada por:

$\underset{\vec{w},b}{min} \underset{\vec{a}\geq 0}{max} \frac{1}{2}\left \| w \right \|^{2} - \sum_{j}a_j\left [ \left ( \vec{w} \cdot \vec{x}_{j} \right )y_j - 1 \right ]$

Ahora, de acuerdo con el principio de dualidad, el problema de optimización anterior puede verse tanto como primario (minimizandob) maximizar

$\underset{\vec{a}\geq 0}{max}\underset{\vec{w},b}{min} \frac{1}{2}\left \| w \right \|^{2} - \sum_{j}a_j\left [ \left ( \vec{w} \cdot \vec{x}_{j} \right )y_j - 1 \right ]$

La condición de Slater para la optimización convexa garantiza que estos dos son problemas iguales.

Para obtener el valor mínimo de w y b, la derivada parcial de primer orden de estas variables debe ser 0:

$\frac{\partial L}{\partial w} = w -\sum_j a_j y_j x_j =0 \\ w = \sum_j a_j y_j x_j \\ \\ \\ Wrt \, b \\ \\ \frac{\partial L}{\partial b} = -\sum_j a_j y_j =0 \\ \\ \sum_j a_j y_j =0$

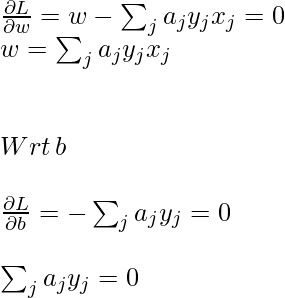
Ahora, coloque la ecuación anterior en la ecuación del multiplicador de Lagrange y simplifique.

$L = \frac{1}{2}\left ( \sum_i \alpha_i y_i x_i \right )\cdot\left ( \sum_j \alpha_j y_j x_j \right ) - \left ( \sum_i \alpha_i y_i x_i \right )\cdot\left ( \sum_j \alpha_j y_j x_j \right ) - \sum_i\left ( \alpha_i y_i b \right ) + \sum_i\left ( \alpha_{i} \right ) \\$

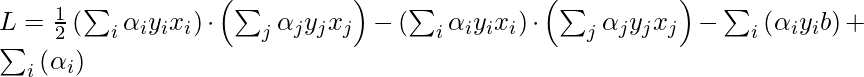
En la ecuación anterior, el término

$\sum_i\left ( \alpha_i y_i b \right ) = 0$
porque,
b
es solo una constante y el resto es de la ecuación anterior”
$L = \sum \alpha_i - \frac{1}{2}\sum_i \sum_j \alpha_{i} \alpha_{j} y_i y_j \left ( x_i \cdot x_j \right ) \alpha_j \geq 0 \forall j$

Para encontrar b, también podemos usar la ecuación anterior y la restricción

$\alpha_j > 0 \,for \,some\, j$
:
$y_j\left ( \vec{w}\cdot\vec{x} + b \right ) = 1 \\ \\ y_jy_j\left ( \vec{w}\cdot\vec{x} + b \right ) = y_j \\ \\ y_j \in \left \{ -1,1 \right \} \\ \\ \left ( \vec{w}\cdot\vec{x} + b \right ) = y_j \\ \\ b = y_k - w \cdot x_k \forall k where \, \alpha_k > 0$

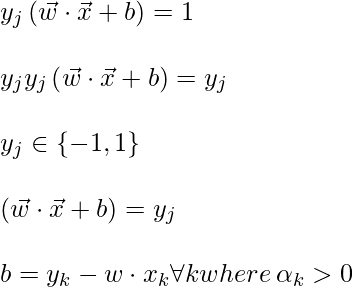
Ahora, la regla de decisión puede estar dada por:

$y_i = sign(\sum \alpha_{i} y_i \left ( \vec{x}_i \cdot \vec{x} \right ) +b )$

Observe que podemos observar a partir de la regla anterior que el multiplicador de Lagrange solo depende del producto escalar de x _i con la variable desconocida x. Este producto escalar se define como la función kernel y se representa por K

$L = \sum \alpha_i - \frac{1}{2}\sum_i \sum_j \alpha_{i} \alpha_{j} y_i y_j K(x_i,x_j) \\ \\ where K = (x_i.x_j)$

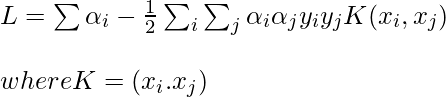
Ahora, para el caso linealmente inseparable, la ecuación dual se convierte en:

$\underset{\alpha}{max} \sum_i \alpha_i - \sum_{i,j} \alpha_i \alpha_j y_i y_j x_i \cdot x_j \\ \\ for, \\ \\ \sum_i \alpha_i y_i =0 \\ \\ 0 \leq \alpha_i \leq C$

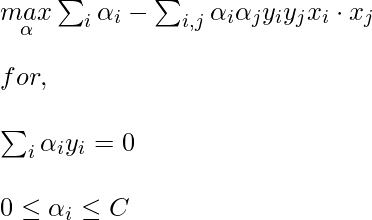
Aquí, agregamos una constante C, es necesaria por las siguientes razones:

Impide el valor de $\alpha$ de $\alpha \to \infty$ .
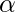
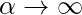
También evita que los modelos se sobreajusten, lo que significa que se pueden aceptar algunos errores de clasificación.

Imagen que representa la transformación

aplicamos la transformación en otro espacio tal que el siguiente. Tenga en cuenta que no necesitamos calcular específicamente la función de transformación, solo necesitamos encontrar el producto escalar de esos para obtener la función kernel, sin embargo, esta función de transformación se puede establecer fácilmente.

$K = \phi(i) \cdot \phi(j)$

dónde,

$\phi()$
es la función de transformación.

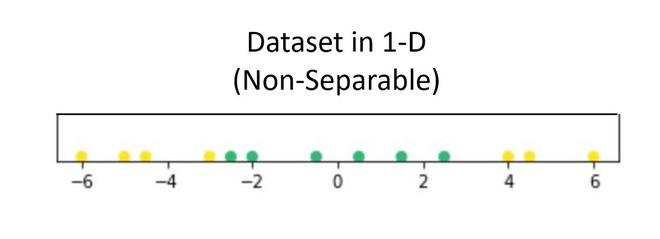
La intuición detrás de que muchas veces los datos pueden estar separados por un hiperplano en una dimensión superior. Veamos esto con más detalle:

Supongamos que tenemos un conjunto de datos que contiene solo 1 variable independiente y 1 dependiente. La siguiente gráfica representa los datos:

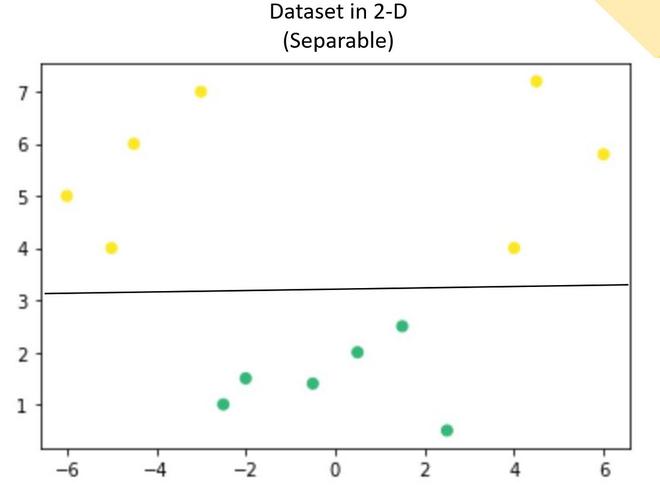
Ahora, en el gráfico anterior, es difícil separar un hiperplano 1D (punto) que separa claramente los puntos de datos de diferentes clases. Pero cuando esto se transformó a 2d usando alguna transformación, brinda opciones para separar las clases.

En el ejemplo anterior, podemos ver que una línea SVM puede separar claramente las dos clases del conjunto de datos.

Hay un núcleo famoso que se usa con bastante frecuencia:

Polinomios de grado =n

$K(u,v) = (u \cdot v)^{n}$

Polinomios de grado hasta n

$K(u,v) = (u \cdot v + 1)^{n}$

Núcleo gaussiano/RBF

$K(\vec{u}, \vec{v}) = e^{-\frac{\left \| \vec{u}-\vec{v} \right \|_{2}^{2}}{2 \sigma^2}}$

Implementación

Python3

# code
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
  
# import some data
cancer = datasets.load_breast_cancer()
X = cancer.data[:,:2]
Y = cancer.target
  
X.shape, Y.shape
  
# perform svm with different kernel, here c is the regularizer
h = .02
C=100
lin_svc = svm.LinearSVC(C=C)
svc = svm.SVC(kernel='linear', C=C)
rbf_svc = svm.SVC(kernel='rbf', gamma=0.7, C=C)
poly_svc = svm.SVC(kernel='poly', degree=3, C=C)
  
# Fit the training dataset.
lin_svc.fit(X, Y)
svc.fit(X, Y)
rbf_svc.fit(X, Y)
poly_svc.fit(X, Y)
  
# plot the results
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),np.arange(y_min, y_max, h))
  
titles = ['linear kernel',
          'LinearSVC (linear kernel)',
          'RBF kernel',
          'polynomial (degree 3) kernel']
  
plt.figure(figsize=(10,10))
  
for i, clf in enumerate((svc, lin_svc,rbf_svc, poly_svc )):
    # Plot the decision boundary using the above meshgrid we generated
    plt.subplot(2, 2, i + 1)
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
  
    # Put the result into a color plot
    Z = Z.reshape(xx.shape)
    plt.set_cmap(plt.cm.flag_r)
    plt.contourf(xx, yy, Z)
  
    # Plot also the training points
    plt.scatter(X[:, 0], X[:, 1], c=Y)
  
    plt.title(titles[i])
  
plt.show()

((569, 2), (569,))

SVM usando diferentes núcleos.

Referencias:

MIT OCW portaobjetos SVM

Publicación traducida automáticamente

Artículo escrito por pawangfg y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Implementación

Python3

Referencias:

Deja una respuesta Cancelar la respuesta