Dado un círculo con un radio dado tiene su centro en una posición particular en el plano de coordenadas. En el plano de coordenadas, se da otro punto. La tarea es encontrar la distancia más corta entre el punto y el círculo.
Ejemplos:
Input: x1 = 4, y1 = 6, x2 = 35, y2 = 42, r = 5 Output: 42.5079 Input: x1 = 0, y1 = 0, x2 = 5, y2 = 12, r = 3 Output: 10

Enfoque :
- Sea el radio del círculo = r
- coordenada del centro del circulo = (x1, y1)
- coordenada del punto = (x2, y2)
- sea la distancia entre el centro y el punto = d
- Como la línea AC interseca al círculo en B, entonces la distancia más corta será BC,
que es igual a (dr)
- aquí usando la fórmula de la distancia,
d = √((x2-x1)^2 – (y2-y1)^2)
- entonces BC = √((x2-x1)^2 – (y2-y1)^2) – r
- asi que,
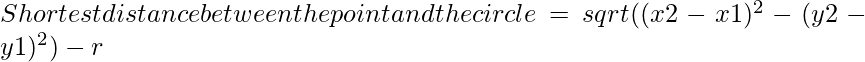
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to find
// the Shortest distance
// between a point and
// a circle
#include <bits/stdc++.h>
using namespace std;
// Function to find the shortest distance
void dist(double x1, double y1, double x2, double y2, double r)
{
cout << "The shortest distance "
<< "between a point and a circle is "
<< sqrt((pow((x2 - x1), 2))
+ (pow((y2 - y1), 2)))
- r
<< endl;
}
// Driver code
int main()
{
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
return 0;
}
Java
// Java program to find
// the Shortest distance
// between a point and
// a circle
class GFG
{
// Function to find the shortest distance
static void dist(double x1, double y1, double x2,
double y2, double r)
{
System.out.println("The shortest distance "
+ "between a point and a circle is "
+ (Math.sqrt((Math.pow((x2 - x1), 2))
+ (Math.pow((y2 - y1), 2)))
- r));
}
// Driver code
public static void main(String[] args)
{
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
}
}
/* This code contributed by PrinciRaj1992 */
Python3
# Python program to find
# the Shortest distance
# between a point and
# a circle
# Function to find the shortest distance
def dist(x1, y1, x2, y2, r):
print("The shortest distance between a point and a circle is "
,((((x2 - x1)** 2) + ((y2 - y1)** 2))**(1/2)) - r);
# Driver code
x1 = 4;
y1 = 6;
x2 = 35;
y2 = 42;
r = 5;
dist(x1, y1, x2, y2, r);
# This code has been contributed by 29AjayKumar
C#
// C# program to find the Shortest distance
// between a point and a circle
using System;
class GFG
{
// Function to find the shortest distance
static void dist(double x1, double y1, double x2,
double y2, double r)
{
Console.WriteLine("The shortest distance "
+ "between a point and a circle is "
+ (Math.Sqrt((Math.Pow((x2 - x1), 2))
+ (Math.Pow((y2 - y1), 2)))
- r));
}
// Driver code
public static void Main(String[] args)
{
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
}
}
/* This code contributed by PrinciRaj1992 */
PHP
<?php
// PHP program to find
// the Shortest distance
// between a point and
// a circle
// Function to find the shortest distance
function dist($x1, $y1, $x2, $y2, $r)
{
echo "The shortest distance between a point and a circle is "
,sqrt((pow(($x2 - $x1), 2))
+ (pow(($y2 - $y1), 2)))
- $r ;
}
// Driver code
$x1 = 4;
$y1 = 6;
$x2 = 35;
$y2 = 42;
$r = 5;
dist($x1, $y1, $x2, $y2, $r);
// This code is contributed by AnkitRai01
?>
Javascript
<script>
// javascript program to find
// the Shortest distance
// between a point and
// a circle
// Function to find the shortest distance
function dist(x1 , y1 , x2, y2 , r)
{
document.write("The shortest distance "
+ "between a point and a circle is "
+ (Math.sqrt((Math.pow((x2 - x1), 2))
+ (Math.pow((y2 - y1), 2)))
- r).toFixed(5));
}
// Driver code
var x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
// This code contributed by Princi Singh
</script>
Producción:
The shortest distance between a point and a circle is 42.5079
Complejidad de tiempo: O(1)
Espacio Auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por IshwarGupta y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA