Distancia entre un punto y un Plano en 3D

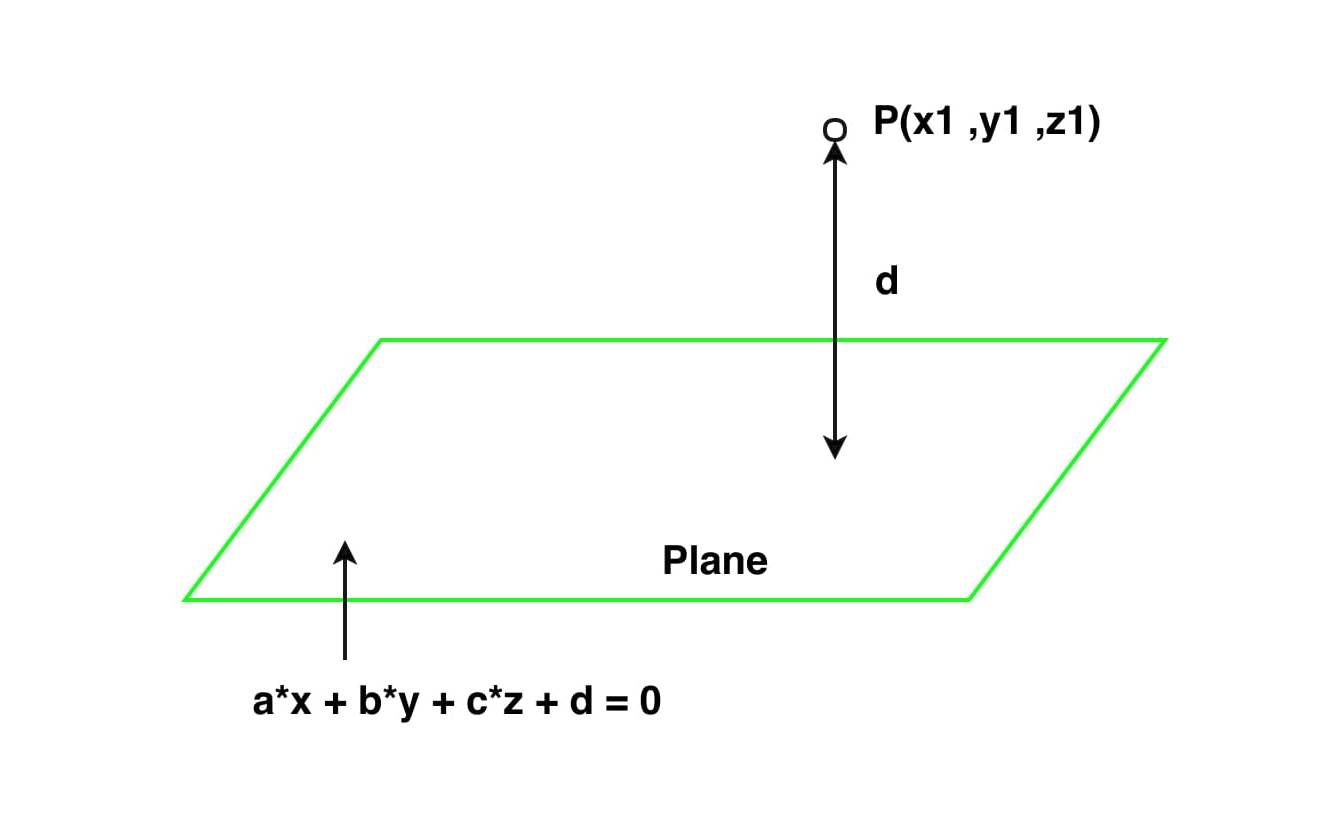
Te dan puntos (x1, y1, z1) y un plano a * x + b * y + c * z + d = 0. La tarea es encontrar la distancia perpendicular (más corta) entre ese punto y el plano dado.
 

Ejemplos: 
 

Entrada: x1 = 4, y1 = -4, z1 = 3, a = 2, b = -2, c = 5, d = 8 
Salida: la distancia perpendicular es 6,78902858227
Entrada: x1 = 2, y1 = 8, z1 = 5 , a = 1, b = -2, c = -2, d = -1 
Salida: La distancia perpendicular es 8.33333333333 

Aproximación: La distancia perpendicular (es decir, la distancia más corta) desde un punto dado hasta un plano es la distancia perpendicular desde ese punto hasta el plano dado. Sea la coordenada del punto dado (x1, y1, z1) 
y la ecuación del plano dada por la ecuación a * x + b * y + c * z + d = 0, donde a, b y c son constantes reales.
La fórmula para la distancia entre un punto y el Plano en 3-D está dada por:
 

Distance = (| a*x1 + b*y1 + c*z1 + d |) / (sqrt( a*a + b*b + c*c))

A continuación se muestra la implementación de las fórmulas anteriores: 
 

// C++ program to find the
// Perpendicular(shortest)
// distance between a point
// and a Plane in 3 D.
#include<bits/stdc++.h>
#include<math.h>
 
using namespace std;
 
// Function to find distance
void shortest_distance(float x1, float y1,
                       float z1, float a,
                       float b, float c,
                       float d)
{
    d = fabs((a * x1 + b * y1 +
              c * z1 + d));
    float e = sqrt(a * a + b *
                   b + c * c);
    cout << "Perpendicular distance is "
         << (d / e);
        return;
}
 
// Driver Code
int main()
{
    float x1 = 4;
    float y1 = -4;
    float z1 = 3;
    float a = 2;
    float b = -2;
    float c = 5;
    float d = 8;
 
    // Function call
    shortest_distance(x1, y1, z1,
                      a, b, c, d);
}
 
// This code is contributed
// by Akanksha Rai(Abby_akku)

// C program to find the Perpendicular(shortest)
// distance between a point and a Plane in 3 D.
 
#include<stdio.h>
#include<math.h>
 
// Function to find distance
void shortest_distance(float x1, float y1, float z1,
                    float a, float b, float c, float d)
{
    d = fabs((a * x1 + b * y1 + c * z1 + d));
    float e = sqrt(a * a + b * b + c * c);
    printf("Perpendicular distance is %f", d/e);
        return;
}
 
// Driver Code
int main()
{
    float x1 = 4;
    float y1 = -4;
    float z1 = 3;
    float a = 2;
    float b = -2;
    float c = 5;
    float d = 8;
 
    // Function call
    shortest_distance(x1, y1, z1, a, b, c, d);
}
// This code is contributed
// by Amber_Saxena.

// Java program to find the
// Perpendicular(shortest)
// distance between a point
// and a Plane in 3 D.
import java .io.*;
 
class GFG
{
     
// Function to find distance
static void shortest_distance(float x1, float y1,
                              float z1, float a,
                              float b, float c,
                              float d)
{
    d = Math.abs((a * x1 + b *
                 y1 + c * z1 + d));
    float e = (float)Math.sqrt(a * a + b *
                               b + c * c);
    System.out.println("Perpendicular distance " +
                                   "is " + d / e);
}
 
// Driver code
public static void main(String[] args)
{
    float x1 = 4;
    float y1 = -4;
    float z1 = 3;
    float a = 2;
    float b = -2;
    float c = 5;
    float d = 8;
 
    // Function call
    shortest_distance(x1, y1, z1,
                      a, b, c, d);
}
}
 
// This code is contributed
// by Amber_Saxena.

# Python program to find the Perpendicular(shortest)
# distance between a point and a Plane in 3 D.
 
import math
 
# Function to find distance
def shortest_distance(x1, y1, z1, a, b, c, d):
     
    d = abs((a * x1 + b * y1 + c * z1 + d))
    e = (math.sqrt(a * a + b * b + c * c))
    print("Perpendicular distance is", d/e)
     
 
# Driver Code
x1 = 4
y1 = -4
z1 = 3
a = 2
b = -2
c = 5
d = 8
 
# Function call
shortest_distance(x1, y1, z1, a, b, c, d)     

// C# program to find the
// Perpendicular(shortest)
// distance between a point
// and a Plane in 3 D.
using System;
 
class GFG
{
     
// Function to find distance
static void shortest_distance(float x1, float y1,
                              float z1, float a,
                              float b, float c,
                              float d)
{
    d = Math.Abs((a * x1 + b *
                   y1 + c * z1 + d));
    float e = (float)Math.Sqrt(a * a + b *
                               b + c * c);
    Console.Write("Perpendicular distance " +
                              "is " + d / e);
}
 
// Driver code
public static void Main()
{
    float x1 = 4;
    float y1 = -4;
    float z1 = 3;
    float a = 2;
    float b = -2;
    float c = 5;
    float d = 8;
 
    // Function call
    shortest_distance(x1, y1, z1,
                      a, b, c, d);
}
}
 
// This code is contributed
// by ChitraNayal

<?php
// PHP program to find the
// Perpendicular(shortest)
// distance between a point
// and a Plane in 3 D.
 
// Function to find distance
function shortest_distance($x1, $y1, $z1,
                           $a, $b, $c, $d)
{
    $d = abs(($a * $x1 + $b * $y1 +
              $c * $z1 + $d));
    $e = sqrt($a * $a + $b *
              $b + $c * $c);
    echo "Perpendicular distance is ". $d / $e;
}
 
// Driver Code
$x1 = 4;
$y1 = -4;
$z1 = 3;
$a = 2;
$b = -2;
$c = 5;
$d = 8;
     
// function call
shortest_distance($x1, $y1, $z1,
                  $a, $b, $c, $d);
 
// This code is contributed
// by Amber_Saxena.
?>

<script>
 
 
// Javascript program to find the
// Perpendicular(shortest)
// distance between a point
// and a Plane in 3 D.
 
// Function to find distance
function shortest_distance( x1,  y1, z1,  a,
                        b,  c, d)
{
    d = Math.abs((a * x1 + b * y1 +
              c * z1 + d));
    let e = Math.sqrt(a * a + b *
                   b + c * c);
    document.write("Perpendicular distance is "
         + (d / e));
        return;
}
 
    // driver code    
    let x1 = 4;
    let y1 = -4;
    let z1 = 3;
    let a = 2;
    let b = -2;
    let c = 5;
    let d = 8;
 
    // Function call
    shortest_distance(x1, y1, z1,
                      a, b, c, d);
     
 // This code is contributed by jana_sayantan.  
</script>

Perpendicular distance is 6.78902858227