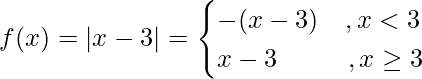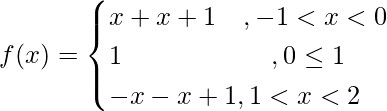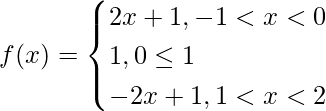Clase 12 Soluciones RD Sharma – Capítulo 10 Diferenciabilidad – Ejercicio 10.1

Pregunta 1. Demuestra que f(x) = |x – 3| es continua pero no diferenciable en x = 3.

Solución:

$f(x) = |x - 3| = \begin{cases}-(x - 3)\ \ \ , x<3\\x - 3\ \ \ \ \ \ \ \ , x\ge 3\end{cases}$

f(3) = 3 – 3 = 0

$LHL = lim_{x\to3^-}f(x)$

$= lim_{h\to0}f(3-h)$

= $lim_{h\to0}(h)$

= 0

$RHL = lim_{x\to3^+}f(x)$

$= lim_{h\to0}f(3+h)$

$= lim_{h\to0}(h)$

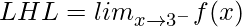
= 0

Como LHL = RHL, f(x) es continua en x = 3.

Ahora, $LHD at (x = 3) = lim_{x\to3^-}\frac{f(x)-f(3)}{x-3}$

$= lim_{h\to0}\frac{h}{-h}$

= –1

$RHD at (x = 3) = lim_{x\to3^+}\frac{f(x)-f(3)}{x-3}$

$= lim_{h\to0}\frac{h}{h}$

= 1

Dado que (LHD en x = 3) ≠ (RHD en x = 3)

f(x) es continua pero no derivable en x =3.

Pregunta 2. Muestre que f (x) = x ^1/3 no es diferenciable en x = 0.

Solución:

(LHD en x = 0) = $lim_{x\to0^-}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{f(0-h)-f(0)}{0-h-0}$

$= lim_{h\to0}(-1)^{-2/3}h^{-2/3}$

= Indefinido

(RHD en x = 0) = $lim_{x\to0^+}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{f(0+h)-f(0)}{0+h-0}$

$= lim_{h\to0}h^{-2/3}$

= Indefinido

Claramente LHD y RHD no existen en 0.

f(x) no es diferenciable en x = 0.

Pregunta 3. Demuestra que 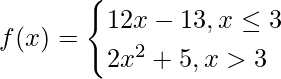$f(x) = \begin{cases}12x-13,x\le3\\2x^2+5,x>3\end{cases}$ es diferenciable en x = 3.

Solución:

(LHD en x = 3) = $lim_{x\to3^-}\frac{f(x)-f(3)}{x-3}$

$= lim_{h\to0}\frac{(-12h)}{-h}$

= 12

RHD en x = 3 = $lim_{x\to3^+}\frac{f(x)-f(3)}{x-3}$

$= lim_{h\to0}\frac{h(2h+12)}{h}$

= 12

Dado que LHL = RHL

f(x) es diferenciable en x = 3.

Pregunta 4. Muestre que la función f se define de la siguiente manera y es continua en x = 2, pero no diferenciable allí:

$f(x) = \begin{cases}3x-2\ \ \ \ \ \ \ \ \ \ ,0<x\le1\\2x^2-2\ \ \ \ \ \ \ \ ,1<x\le2\\5x-4\ \ \ \ \ \ \ \ \ \ ,x>2\end{cases}$

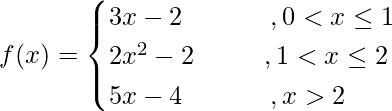
Solución:

f(2) = 2(2) ² – 2 = 6

$LHL = lim_{x\to2^-}f(2-h)$

$= lim_{h\to0}[2(2-h)^2-(2-h)]$

= 8 – 2

= 6

$RHL = lim_{x\to2^+}f(x)$

$= lim_{h\to0}f(2+h)$

$= lim_{h\to0}5(2+h) - 4$

= 6

Claramente LHL = RHL en x = 2

Por tanto, f(x) es derivable en x = 2.

Pregunta 5. Discuta la continuidad y diferenciabilidad de la función f(x) = |x| + |x-1| en el intervalo de (-1, 2).

Solución:

$f(x) = \begin{cases}x+x+1\ \ \ ,-1<x<0\\1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,0\lex\le1\\-x-x+1,1<x<2\end{cases}$

$f(x) = \begin{cases}2x+1,-1<x<0\\1,0\lex\le1\\-2x+1,1<x<2\end{cases}$

(LHD en x = 0) = $lim_{x\to0^-}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{2x}{x}$

= 2

(RHD en x = 0) = $lim_{x\to0^+}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{0}{x}$

= 0

Por tanto, f(x) no es diferenciable en x = 0.

Pregunta 6. Encuentra si la siguiente función es diferenciable en x = 1 y x = 2 o no.

$f(x) = \begin{cases}x\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x\le1\\2-x\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,1\lex\le2\\-2+3x-x^2\ \ ,x>2\end{cases}.$

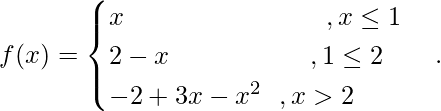
Solución:

(LHD en x = 1) = $lim_{x\to1^-}\frac{f(x)-f(1)}{x-1}$

$= lim_{x\to1^-}\frac{x-1}{x-1}$

= 1

(RHD en x = 1) = $lim_{x\to1^+}\frac{f(x)-f(1)}{x-1}$

$= lim_{x\to1^+}\frac{1-x}{x-1}$

= –1

Claramente LHD ≠ RHD en x = 1

Entonces f(x) no es derivable en x = 1.

(LHD en x = 2) = $lim_{x\to2^-}\frac{f(x)-f(2)}{x-2}$

$= lim_{x\to2^-}\frac{2-x}{x-2}$

= –1

(RHD en x = 2) = $lim_{x\to2^+}\frac{f(x)-f(2)}{x-2}$

$= lim_{x\to2^+}(1-x)$

= –1

Claramente LHL = RHL en x = 2

Por tanto, f(x) es derivable en x = 2.

Pregunta 7(i). Demostrar que $f(x) = \begin{cases}x^msin[\frac{1}{x}],x≠0\\0\ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=0\end{cases}$ es diferenciable en x = 0, si m>1.

Solución:

(LHD en x = 0) = $lim_{x\to0^-}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{f(0-h)-f(0)}{0-h-0}$

$= lim_{h\to0}\frac{(-h)^msin[\frac{-1}{h}]-0}{-h}$

= 0 × k

= 0

(RHD en x = 0) $= lim_{x\to0^+}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{(0+h)-f(0)}{0+h-0}$

$= lim_{h\to0}\frac{(h)^msin[\frac{-1}{h}]-0}{-h}$

= 0 × k

= 0

Claramente LHL = RHL en x = 0

Por tanto, f(x) es derivable en x = 0.

Pregunta 7(ii) Demuestra que $f(x) = \begin{cases}x^msin[\frac{1}{x}],x≠0\\0\ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=0\end{cases}$ no es diferenciable en x = 0, si 0<m<1.

Solución:

(LHD en x = 0) $= lim_{x\to0^-}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{f(0-h)-f(0)}{0-h-0}$

$= lim_{h\to0}\frac{(-h)^msin[\frac{-1}{h}]-0}{-h}$

= No definido

(RHD en x = 0) $= lim_{x\to0^+}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{(0+h)-f(0)}{0+h-0}$

$= lim_{h\to0}\frac{(h)^msin[\frac{-1}{h}]-0}{-h}$

= No definido

Claramente f(x) no es diferenciable en x = 0.

Pregunta 7(iii) Demuestre que $f(x) = \begin{cases}x^msin[\frac{1}{x}],x≠0\\0\ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=0\end{cases}$ no es diferenciable en x = 0 , si m≤0.

Solución:

(LHD en x = 0) $= lim_{x\to0^-}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{f(0-h)-f(0)}{0-h-0}$

$= lim_{h\to0}\frac{(-h)^msin[\frac{-1}{h}]-0}{-h}$

= No definido

(RHD en x = 0) $= lim_{x\to0^+}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{(0+h)-f(0)}{0+h-0}$

$= lim_{h\to0}\frac{(h)^msin[\frac{-1}{h}]-0}{-h}$

= No definido

Claramente f(x) no es diferenciable en x = 0.

Pregunta 8. Encuentra el valor de a y b para que la función 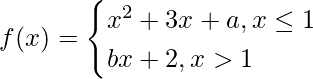$f(x)= \begin{cases}x^2+3x+a,x\le1\\bx+2,x>1\end{cases}$ sea diferenciable en cada valor real de x.

Solución:

(LHD en x = 1) = $lim_{x\to1^-}\frac{f(x)-f(1)}{x-1}$

$= lim_{h\to0}\frac{h^2-5h}{-h}$

= 5

(RHD en x = 2) = $lim_{x\to1^+}\frac{f(x)-f(1)}{x-1}$

$= lim_{h\to0}\frac{b+bh+2-b-2}{h}$

= segundo

Como f(x) es derivable en x = 1, entonces

segundo = 5

Por lo tanto, 4 + a = b + 2

o, a = 7 – 4 = 3

Por lo tanto, a = 3 y b = 5.

Pregunta 9. Muestre que la función $f(x) = \begin{cases}|2x-3|[x]\ \ \ \ \ \ \ \ ,x\ge 1\\sin[\frac{πx}{2}]\ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x<1\end{cases}$ no es derivable en x = 1.

Solución:

(LHD en x = 1) = $lim_{x\to1^-}\frac{f(x)-f(1)}{x-1}$

$= lim_{h\to0}\frac{f(1-h)-1}{1-h-1}$

$= lim_{h\to0}\frac{cos[πh/2]-1}{-h/2}$

= 0

(RHD en x = 1) = $lim_{x\to1^+}\frac{f(x)-f(1)}{x-1}$

$= lim_{h\to0}\frac{f(1+h)-f(1)}{1+h-1}$

$= lim_{h\to0}\frac{-2-2h+3-1}{h}$

= –2

Dado que (LHD en x = 1) ≠ (RHD en x = 1)

f(x) es continua pero no derivable en x =1.

Pregunta 10. Si 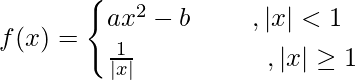$f(x) = \begin{cases}ax^2-b\ \ \ \ \ \ \ ,|x|<1\\\frac{1}{|x|}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,|x|\ge 1\end{cases}$ es diferenciable en x = 1, encuentra a y b.

Solución:

Sabemos que f(x) es continua en x = 1.

Entonces, a – b = 1 …..(1)

(LHD en x = 1) = $lim_{x\to1^-}\frac{f(x)-f(1)}{x-1}$

$= lim_{h\to0}\frac{a(1-h)^2-(a-1)-1}{-h}$

Usando (1), obtenemos

$= lim_{h\to0}(2a-ah)$

= 2a

(RHD en x = 1) $= lim_{x\to1^+}\frac{f(x)-f(1)}{x-1}$

$= lim_{h\to0}\frac{-1}{1+h}$

= –1

Como f(x) es diferenciable, LHL = RHL

o, 2a = –1

a = –1/2

Sustituyendo a = –1/2 en (1), obtenemos,

b = –1/2 – 1

b = –3/2

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Demuestra que f(x) = |x – 3| es continua pero no diferenciable en x = 3.

Pregunta 2. Muestre que f (x) = x 1/3 no es diferenciable en x = 0.

Pregunta 3. Demuestra que es diferenciable en x = 3.

Pregunta 4. Muestre que la función f se define de la siguiente manera y es continua en x = 2, pero no diferenciable allí:

Pregunta 5. Discuta la continuidad y diferenciabilidad de la función f(x) = |x| + |x-1| en el intervalo de (-1, 2).

Pregunta 6. Encuentra si la siguiente función es diferenciable en x = 1 y x = 2 o no.

Pregunta 7(i). Demostrar que es diferenciable en x = 0, si m>1.

Pregunta 7(ii) Demuestra que no es diferenciable en x = 0, si 0<m<1.

Pregunta 7(iii) Demuestre que no es diferenciable en x = 0 , si m≤0.

Pregunta 8. Encuentra el valor de a y b para que la función sea diferenciable en cada valor real de x.

Pregunta 9. Muestre que la función no es derivable en x = 1.

Pregunta 10. Si es diferenciable en x = 1, encuentra a y b.

Deja una respuesta Cancelar la respuesta

Pregunta 2. Muestre que f (x) = x ^1/3 no es diferenciable en x = 0.

Pregunta 3. Demuestra que $f(x) = \begin{cases}12x-13,x\le3\\2x^2+5,x>3\end{cases}$ es diferenciable en x = 3.

Pregunta 7(i). Demostrar que $f(x) = \begin{cases}x^msin[\frac{1}{x}],x≠0\\0\ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=0\end{cases}$ es diferenciable en x = 0, si m>1.

Pregunta 7(ii) Demuestra que $f(x) = \begin{cases}x^msin[\frac{1}{x}],x≠0\\0\ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=0\end{cases}$ no es diferenciable en x = 0, si 0<m<1.

Pregunta 7(iii) Demuestre que $f(x) = \begin{cases}x^msin[\frac{1}{x}],x≠0\\0\ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=0\end{cases}$ no es diferenciable en x = 0 , si m≤0.

Pregunta 8. Encuentra el valor de a y b para que la función $f(x)= \begin{cases}x^2+3x+a,x\le1\\bx+2,x>1\end{cases}$ sea diferenciable en cada valor real de x.

Pregunta 9. Muestre que la función $f(x) = \begin{cases}|2x-3|[x]\ \ \ \ \ \ \ \ ,x\ge 1\\sin[\frac{πx}{2}]\ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x<1\end{cases}$ no es derivable en x = 1.

Pregunta 10. Si $f(x) = \begin{cases}ax^2-b\ \ \ \ \ \ \ ,|x|<1\\\frac{1}{|x|}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,|x|\ge 1\end{cases}$ es diferenciable en x = 1, encuentra a y b.