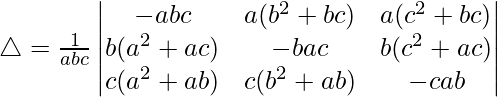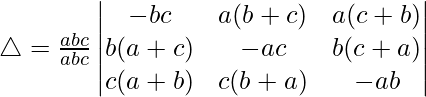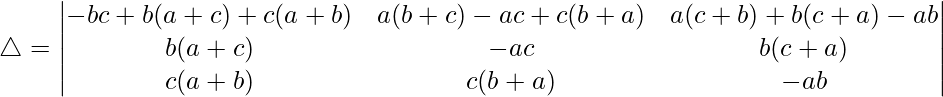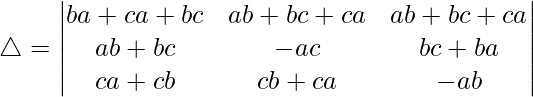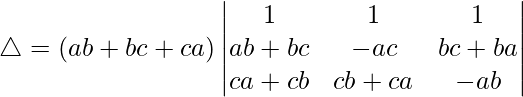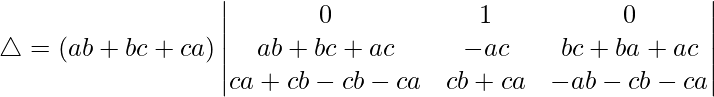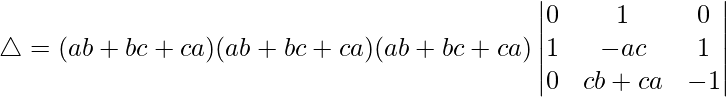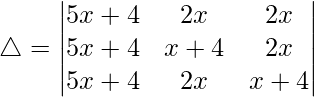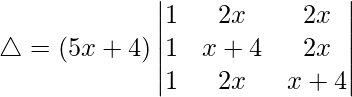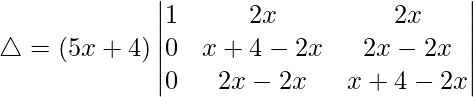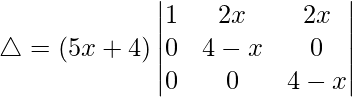Acreditar las siguientes identidades:
Pregunta 18. 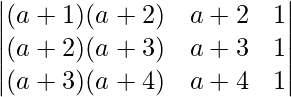 = -2
= -2
Solución:
Teniendo en cuenta el determinante, tenemos
R2⇢R2 – R1 y R3⇢R3 – R2
△ = 1[2(a + 2) – 2(a + 3)]
△ = (4a + 4 – (4a + 6))
△ = (4a + 4 – 4a – 6)
△ = -2
Por lo tanto probado
Pregunta 19. 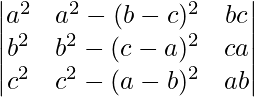 = (a – b)(b – c)(c – a)(a + b + c)(a 2 + b 2 + c 2 )
= (a – b)(b – c)(c – a)(a + b + c)(a 2 + b 2 + c 2 )
Solución:
Teniendo en cuenta el determinante, tenemos
C2⇢C2 – 2C1 – 2C3
Tomando -(a 2 + b 2 + c 2 ) común de C2, obtenemos
R2⇢R2 – R1 y R3⇢R3 – R1
Tomando (b – a) y (c – a) comunes de R1 y R2, obtenemos
△ = -(a 2 + b 2 + c 2 )(b – a)(c – a)[1((-b)(b + a) – (c + a)(-c))]
△ = (a 2 + b 2 + c 2 )(a – b)(c – a)[(-b)(b + a) + (c + a)c]
△ = (a 2 + b 2 + c 2 )(a – b)(c – a)[-b 2 – ab + ac + c 2 ]
△ = (a 2 + b 2 + c 2 )(a – b)(c – a)
△ = (a 2 + b 2 + c 2 )(a – b)(c – a)[(c – b)(c + b) + a(c – b)]
△ = (a 2 + b 2 + c 2 )(a – b)(c – a)(c – b)
△ = (a 2 + b 2 + c 2 )(a + b + c)(a – b)(b – c)(c – a)
Por lo tanto probado
Pregunta 20. 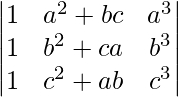 = (a – b)(b – c)(c – a)(a 2 + b 2 + c 2 )
= (a – b)(b – c)(c – a)(a 2 + b 2 + c 2 )
Solución:
Teniendo en cuenta el determinante, tenemos
R2⇢R2 – R1 y R3⇢R3 – R1
Tomando (b – a) y (c – a) comunes de R2 y R3 respectivamente, obtenemos
△ = (b – a)(c – a)[1((b + a – c)(c 2 + a 2 + ac) – (c + a – b)(b 2 + a 2 + ab))]
△ = (b – a)(c – a)(b – c)(a + b + c)
△ = -(a – b)(c – a)(b – c)(a + b + c)
Por lo tanto probado
Pregunta 21.  = 4a 2 b 2 c 2
= 4a 2 b 2 c 2
Solución:
Teniendo en cuenta el determinante, tenemos
Tomando a, b y c comunes de C1, C2 y C3 obtenemos
C1⇢C1 + C2 + C3
Tomando 2 comunes de C1, obtenemos
C2⇢C2 – C1 y C3⇢C3 – C1
C1⇢C1 + C2 + C3
Tomando c, a y b comunes de C1, C2 y C3 obtenemos
R3⇢R3 – R1
△ = 2a 2 segundo 2 do 2 [1((-1)(-1) – (-1)(1))]
△ = 2a 2 segundo 2 do 2 [1 – (-1)]
△ = 2a 2 segundo 2 do 2 [1 + 1]
△ = 4a 2 segundo 2 do 2
Por lo tanto probado
Pregunta 22. 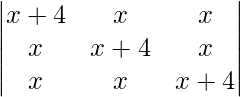 = 16(3x + 4)
= 16(3x + 4)
Solución:
Teniendo en cuenta el determinante, tenemos
C1⇢C1 + C2 + C3
Tomando (3x + 4) común de C1, obtenemos
R2⇢R2 – R1 y R3⇢R3 – R1
△ = (3x + 4)[1((4)(4) – (-4)(0))]
△ = (3x + 4)[16 – 0]
△ = 16(3x + 4)
Por lo tanto probado
Pregunta 23. 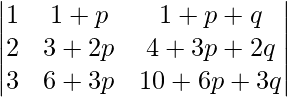 = 1
= 1
Solución:
Teniendo en cuenta el determinante, tenemos
C2⇢C2 – pC1 y C3⇢C3 – qC1
C3⇢C3 – pC2
C2⇢C2 – C1 y C3⇢C3 – C2
△ = 1[(1)(4) – (1)(3)]
△ = [4 – 3]
△ = 1
Por lo tanto probado
Pregunta 24.  = (a + b – c)(b + c – a)(c + a – b)
= (a + b – c)(b + c – a)(c + a – b)
Solución:
Teniendo en cuenta el determinante, tenemos
R1⇢R1 – R2 – R3
Tomando (-a+b+c) común de R1, obtenemos
C2⇢C2 + C1 y C3⇢C3 + C1
△ = (b + c – a)[1((b + a – c)(c + a – b) – (0)(0))]
△ = (b + c – a)[(b + a – c)(c + a – b)]
△ = (b + c – a)(b + a – c)(c + a – b)
Por lo tanto probado
Pregunta 25. 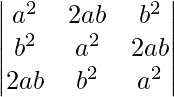 = (a 3 + b 3 ) 2
= (a 3 + b 3 ) 2
Solución:
Teniendo en cuenta el determinante, tenemos
C1⇢C1 + C2 + C3
Tomando (a + b) 2 comunes de C1, obtenemos
R2⇢R2 – R1 y R3⇢R3 – R1
R2⇢R2 – R3
△ = (a + b) 2 [1((a 2 – b 2 )(a 2 – b 2 ) – (b 2 – 2ab)(2ab – a 2 ))]
△ = (a + b) 2 [(a 2 – b 2 ) 2 + (b 2 – 2ab)(a 2 – 2ab)]
△ = (a + b) 2 [(a 2 + b 2 – ab) 2 ]
△ = (un 3 + segundo 3 ) 2
Por lo tanto probado
Pregunta 26. 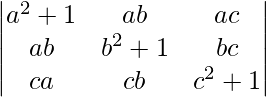 = 1 + a 2 + b 2 + c 2
= 1 + a 2 + b 2 + c 2
Solución:
Teniendo en cuenta el determinante, tenemos
Multiplicando a, b y c por R1, R2 y R3 obtenemos
Tomando a, b y c comunes de C1, C2 y C3 obtenemos
R1⇢R1 + R2 + R3
Tomando (a 2 + b 2 + c 2 + 1) común de R1, obtenemos
C2⇢C2-C1 y C3⇢C3-C1
△ = (a 2 + b 2 + c 2 + 1)[1((1)(1) – (0)(0))]
△ = (un 2 + segundo 2 + c 2 + 1)[1]
△ = (un 2 + segundo 2 + c 2 + 1)
Por lo tanto demostrado !!
Pregunta 27. 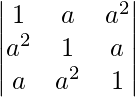 = (a 3 – 1) 2
= (a 3 – 1) 2
Solución:
Teniendo en cuenta el determinante, tenemos
C1⇢C1 + C2 + C3
Tomando (a 2 + a + 1) común de C1, obtenemos
R2⇢R2 – R1 y R3⇢R3 – R1
Tomando (1 – a) común de R2 y R3, obtenemos
△ = (a 2 + a + 1)(1 – a) 2 [1((1 + a)(1) – (a)(-a))]
△ = (un 2 + un + 1)(1 – un) 2 [(1 + un) + un 2 ]
△ = (un 2 + un + 1)(1 – un) 2 [1 + un + un 2 ]
△ = ((un 2 + un + 1)(1 – un)) 2
△ = (un 3 – 1) 2
Por lo tanto probado
Pregunta 28.  = 2(a + b)(b + c)(c + a)
= 2(a + b)(b + c)(c + a)
Solución:
Teniendo en cuenta el determinante, tenemos
C1⇢C1 + C3 y C2⇢C2 + C3
Tomando (c + a) y (b + c) comunes de C1 y C2, obtenemos
R2⇢R2 + R1 y R3⇢R3 + R2
△ = (c + a)(b + c)[1((0)(b + c) – (2)(-a – b))]
△ = (c + a)(b + c)[0 + 2(a + b)]
△ = 2(a + b)(c + a)(b + c)
Por lo tanto probado
Pregunta 29. 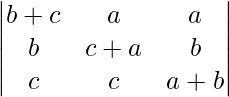 = 4abc
= 4abc
Solución:
Teniendo en cuenta el determinante, tenemos
R1⇢R1 + R2 + R3
Tomando 2 comunes de R1, obtenemos
R2⇢R2 – R1 y R3⇢R3 – R1
R1⇢R1 + R2 + R3
△ = 2[-c((-c)(0) – (-a)(-b)) + b((-c)(-a) – (0)(-b))]
△ = 2[-c(0 – ab) + b(ac – 0)]
△ = 2[abc + abc]
△ = 2[2abc]
△ = 4abc
Por lo tanto probado
Pregunta 30. 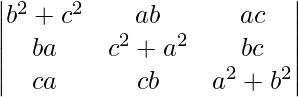 = 4a 2 b 2 c 2
= 4a 2 b 2 c 2
Solución:
Teniendo en cuenta el determinante, tenemos
Multiplicando a, b y c por R1, R2 y R3 respectivamente, obtenemos
Tomando comunes a, b y c a C1, C2 y C3 respectivamente, obtenemos
R1⇢R1 + R2 + R3
Tomando 2 comunes de R1, obtenemos
R1⇢R1 – R2
△ = 2
△ = 2
△ = 2
△ = 2
Pregunta 31. 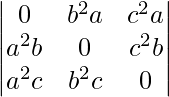 = 2a 3 b 3 c 3
= 2a 3 b 3 c 3
Solución:
Teniendo en cuenta el determinante, tenemos
Tomando a 2 , b 2 y c 2 comunes de C1, C2 y C3. obtenemos
Tomando a, b y c comunes de R1, R2 y R3. obtenemos
C2⇢C2 – C3
△ = un 3 segundo 3 do 3 [1((1)(1) – (1)(-1))]
△ = un 3 segundo 3 do 3 [1 + 1]
△ = 2a 3 segundo 3 do 3
Por lo tanto probado
Pregunta 32. 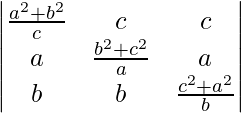 = 4abc
= 4abc
Solución:
Teniendo en cuenta el determinante, tenemos
Multiplicando c, a y b por R1, R2 y R3. Obtenemos
R1⇢R1 – R2 – R3
Tomando -2 común de R1, obtenemos
R2⇢R2 – R1 y R3⇢R3 – R1
△ = 4abc
Por lo tanto probado
Pregunta 33. 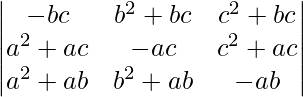 = (ab + bc + ca) 3
= (ab + bc + ca) 3
Solución:
Teniendo en cuenta el determinante, tenemos
Multiplicando a, byc por R1, R2 y R3. Obtenemos
Tomando a, b y c comunes de C1, C2 y C3. obtenemos
R1⇢R1 + R2 + R3
Tomando (ab + bc + ca) común de R1, obtenemos
C1⇢C1 – C2 y C3⇢C3 – C2
Tomando (ab + bc + ca) común de C1 y C2, obtenemos
△ = (ab + bc + ca) 3 [-1((1)(-1) – (1)(0))]
△ = (ab + bc + ca) 3 [-1(-1)]
△ = (ab + bc + ca) 3
Por lo tanto probado
Pregunta 34. 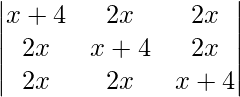 = (5x + 4)(4 -x) 2
= (5x + 4)(4 -x) 2
Solución:
Teniendo en cuenta el determinante, tenemos
C1⇢C1 + C2 + C3
Tomando (5x + 4) común de C1, obtenemos
R2⇢R2 – R1 y R3⇢R3 – R1
△ = (5x + 4)[1((4 – x)(4 – x) – (0)(0))]
△ = (5x + 4)[(4 – x) 2 ]
△ = (5x + 4)(4 – x) 2
Por lo tanto probado
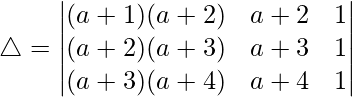
![Rendered by QuickLaTeX.com \triangle = \begin{vmatrix}(a+1)(a+2) & a+2 & 1 \\ (a+2)(a+3)-(a+1)(a+2) & a+3-(a+2) & 0 \\ (a+3)(a+4)-(a+2)(a+3) & a+4-(a+3) & 0 \end{vmatrix}\\ \triangle = \begin{vmatrix}(a+1)(a+2) & a+2 & 1 \\ (a+2)[a+3-a-1] & a+3-a-2 & 0 \\ (a+3)[a+4-a-2] & a+4-a-3 & 0 \end{vmatrix}\\ \triangle = \begin{vmatrix}(a+1)(a+2) & a+2 & 1 \\ 2(a+2) & 1 & 0 \\ 2(a+3) & 1 & 0 \end{vmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-78d86e5948ac8eff568a11ebca525420_l3.png)
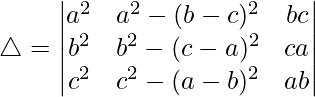
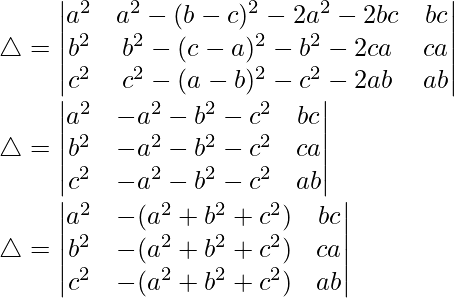
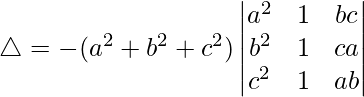
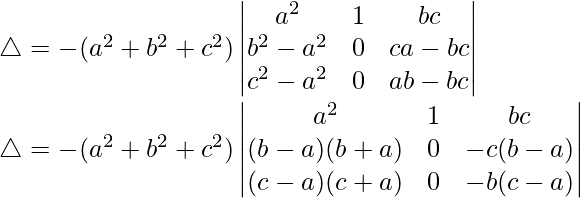
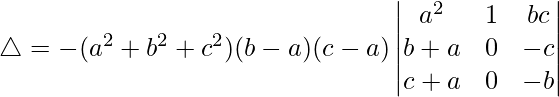
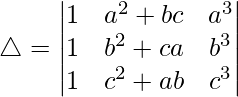
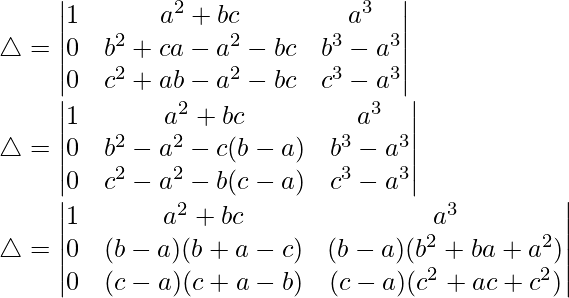
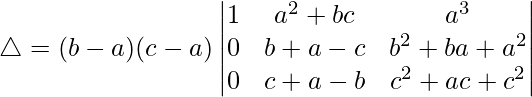
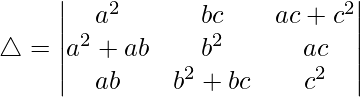
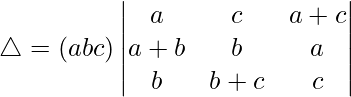

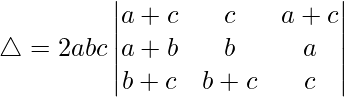
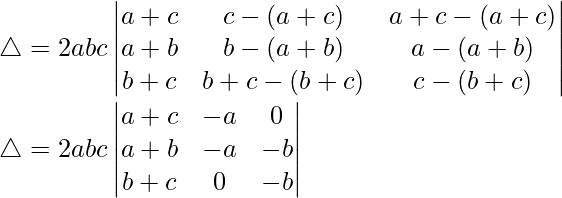
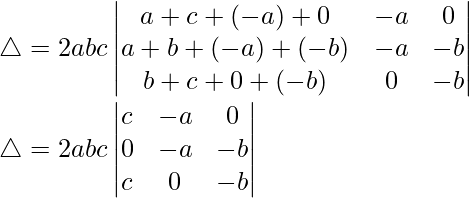
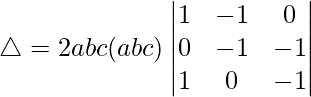
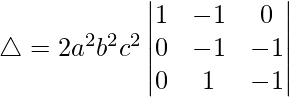
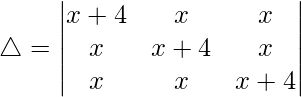
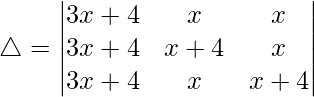
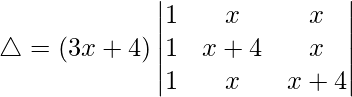
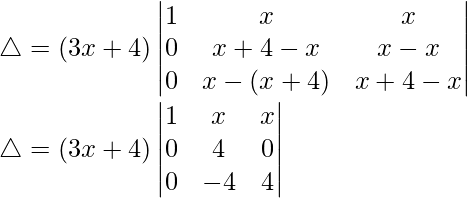
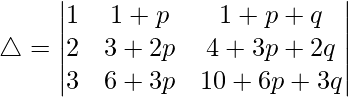
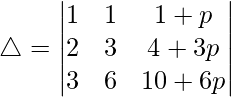
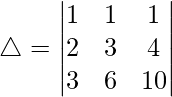
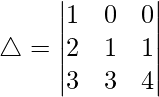
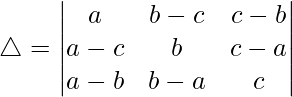
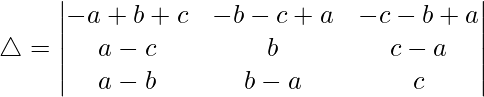
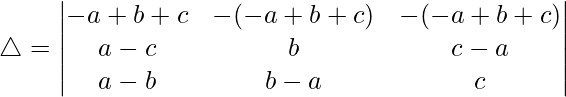
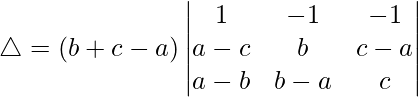

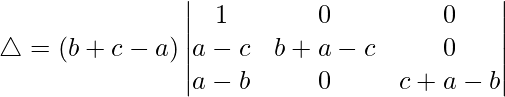
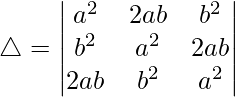
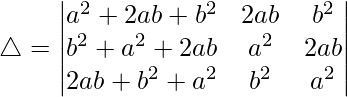
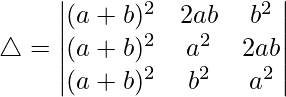
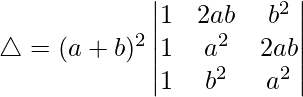
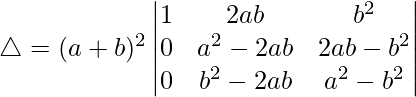
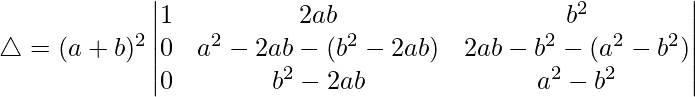
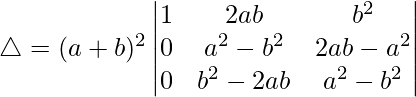

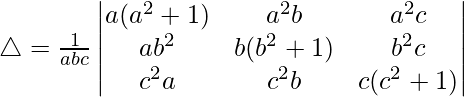
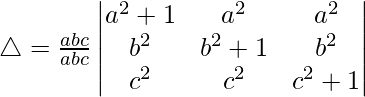
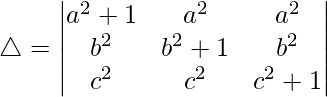
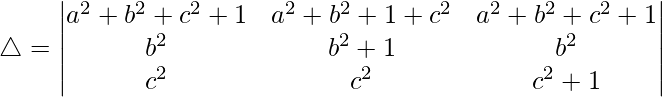


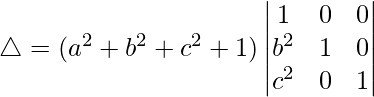

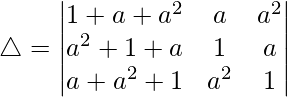
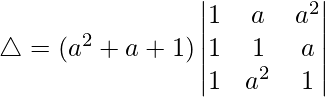
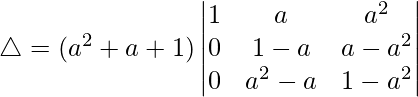
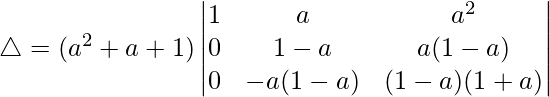
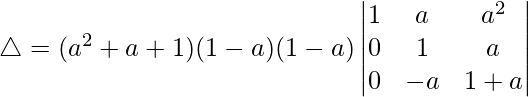
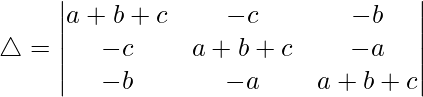
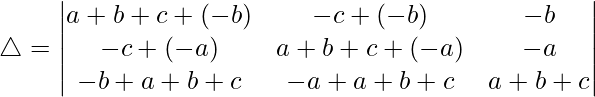
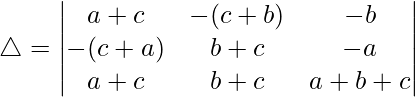
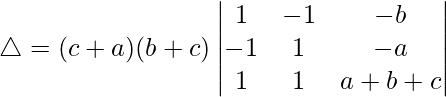

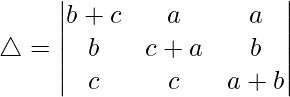


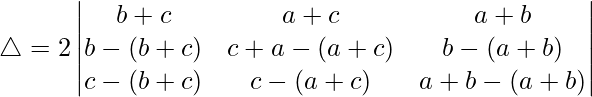
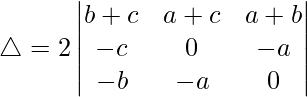
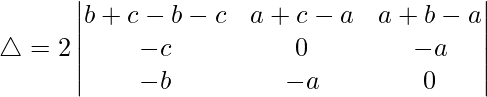
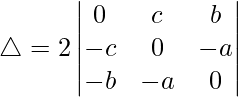
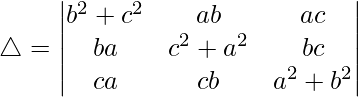
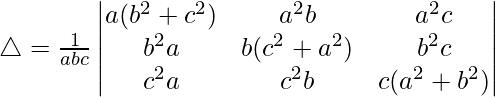
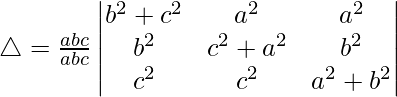
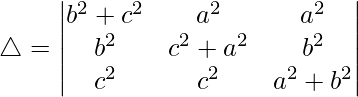

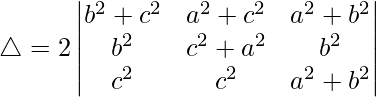
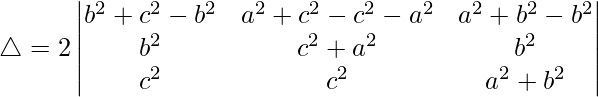
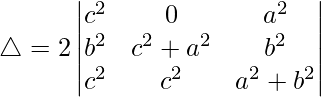
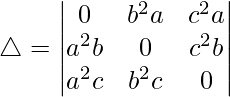

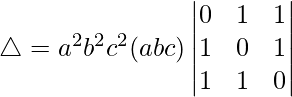
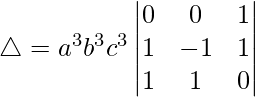
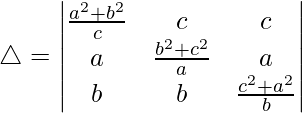
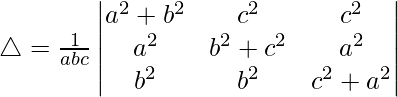
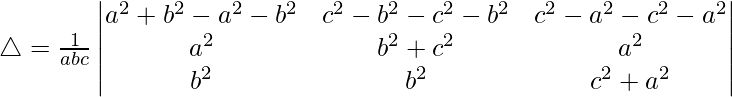

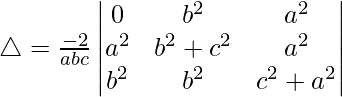
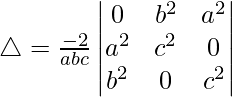
![Rendered by QuickLaTeX.com \triangle = \frac{-2}{abc}[-b^2((a^2)(c^2)-(0)(b^2))+a^2((a^2)(0)-(b^2)(c^2))]\\ \triangle = \frac{-2}{abc}[-b^2(a^2c^2)+a^2(-b^2c^2)]\\ \triangle = \frac{-2}{abc}[-b^2a^2c^2-a^2b^2c^2]\\ \triangle = \frac{-2}{abc}[-2a^2b^2c^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-761ae26328035a31d1407204b527ecea_l3.png)