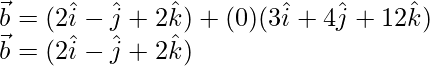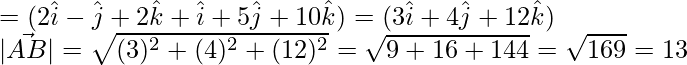Pregunta 8. Encuentra la imagen del punto (1, 3, 4) en el plano 2x – y + z + 3 = 0.
Solución:
Según la pregunta tenemos que encontrar la imagen del punto P(1, 3, 4)
en el plano 2x – y + z +3 = 0
Ahora supongamos que Q sea la imagen del punto.
Aquí, las relaciones de dirección de la normal al plano = 2, -1, 1
Las relaciones de dirección de PQ que es paralela a la normal al plano
es proporcional a 2, -1, 1 y la recta PQ pasa por el punto P(1, 3, 4).
Así, la ecuación de la recta PQ es:
Ahora, el punto general sobre la recta PQ = (2λ + 1, -λ + 3, λ + 4)
Sea Q = (2λ + 1, -λ + 3, λ + 4) -Ecuación(1)
Aquí, Q es la imagen de P, entonces R es el punto medio de PQ
Coordenadas de R =
El punto R se encuentra en el plano 2x – y + z + 3 = 0
= 2(λ + 1) –
4λ + 4 + λ – 6 + λ + 8 + 6 = 0
6λ = -12
λ = -2
Ahora, pon el valor de λ en la ecuación (1), obtenemos
= (-4 + 1, 2 + 3, -2 + 4)
= (-3, 5, 2)
Por lo tanto, la imagen del punto P(1, 3, 4) es (-3, 5, 2)
Pregunta 9. Encuentra la distancia del punto con vector de posición 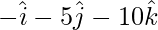 desde el punto de intersección de la línea
desde el punto de intersección de la línea 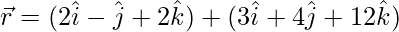 con el plano
con el plano 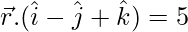 .
.
Solución:
De acuerdo con la pregunta, tenemos que encontrar la distancia de un punto A con posición
vector
desde el punto de intersección de
línea
con avion
Sea el punto de intersección de la línea y el plano
La recta y el plano se cortarán cuando,
(2 + 3λ)(1) + (-1 + 4λ)(-1) + (2 + 12λ)(1) = 5
2 + 3λ + 1 – 4λ + 2 + 12λ = 5
11λ = 5 – 5
λ = 0
Entonces, el punto B está dado por
La distancia requerida es de 13 unidades.
Pregunta 10. Encuentra la longitud y el pie de la perpendicular desde el punto (1, 1, 2) al plano 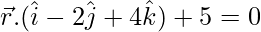 .
.
Solución:
Plano = x – 2y + 4z + 5 = 0 -Ecuación(1)
Punto = (1, 1, 2)
re =
= 12/√21
La longitud de la perpendicular desde el punto dado al plano = 12/√21
Supongamos que el pie de la perpendicular sea (x, y, z).
Entonces los DR son proporcionales
x = k + 1
y = -2k + 1
z = 4k + 2
Sustituye (x, y, z) = (k + 1, -2k + 1, 4k + 2) en la ecuación del plano (1)
k + 1 + 4k – 2 + 16k + 8 + 5 = 0
21k = -12
k = -12/21 = -4/7
Por lo tanto, la coordenada del pie de la perpendicular = (3/7, 15/7, -2/7)
Pregunta 11. Encuentra las coordenadas del pie de la perpendicular y la distancia perpendicular del punto P(3, 2, 1) desde el plano 2x – y + z + 1 = 0. Encuentra también la imagen del punto en el plano .
Solución:
Dado:
Plano = 2x – y + z + 1 = 0 -Ecuación(1)
Punto P = (3, 2, 1)
re =
La distancia perpendicular del punto P al plano(D) = √6
Supongamos que el pie de la perpendicular sea (x, y, z).
Entonces los DR son proporcionales
x = 2k + 3
y = -k + 2
z = k + 1
Sustituye (x, y, z) = (2k + 3, -k + 2, k + 1) en la ecuación del plano (1)
4k + 6 + k – 2 + k + 1 + 1 = 0
6k = -6
k = -6/6 = -1
La coordenada del pie de la perpendicular = (1, 3, 0)
Pregunta 12. Encuentra los cosenos directores del vector unitario perpendicular al plano que 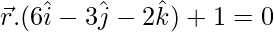 pasa por el origen.
pasa por el origen.
Solución:
Dado:
ecuación del plano
Así, las relaciones de dirección normales al plano son 6, -3 y -2
Por lo tanto, los cosenos directores a la normal al plano son
=
= 6/7, -3/7, -2/7
= -6/7, 3/7, 2/7
Los cosenos directores del vector unitario perpendicular al plano
son iguales a los cosenos directores del vector unitario perpendicular
al plano son: -6/7, 3/7, 2/7
Pregunta 13. Encuentra las coordenadas del pie de la perpendicular trazada desde el origen hasta el plano 2x – 3y + 4z – 6 = 0.
Solución:
Según la pregunta,
Plano = 2x – 3y + 4z – 6 = 0
Las relaciones de dirección de la normal al plano son 2, -3 y 4.
Así, las relaciones de dirección de la línea perpendicular al plano son 2, -3 y 4.
La ecuación de la recta que pasa por (x 1 , y 1 , z 1 ) con relaciones de dirección a, b y c es
Por tanto, la ecuación de la recta que pasa por el origen
con relaciones de dirección 2, -3 y 4 es
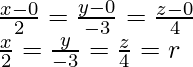
Aquí, r es la misma constante.
Cualquier punto de la recta es de la forma 2r, -3r y 4r,
si el punto P(2r, -3r, 4r) está en el plano 2x – 3y + 4z – 6 = 0.
Así, tenemos,
2(2r) – 3(-3r) + 4(4r) – 6 = 0
4r + 9r + 16r – 6 = 0
29r = 6
r = 6/29
Así, las coordenadas del punto de intersección de la perpendicular
desde el origen y el plano son:
PAG(2×6/29, -3×629, 4×6/29) = PAG(12/29, -18/29, 24/29)
Pregunta 14. Encuentra la longitud y el pie de la perpendicular desde el punto (1, 3/2, 2) al plano 2x – 2y + 4z +5 = 0.
Solución:
Dado:
Punto = (1, 3/2, 2)
Plano = 2x – 2y + 4z + 5 = 0
re =
= √6
Entonces, la longitud de la perpendicular desde el punto al plano (D) = √6
Sea el pie de la perpendicular (x, y, z). Entonces, los DR son proporcionales
x = 2k + 1
y = -2k + 3/2
z = 4k + 2
Entonces, usando los valores de x, y, z en la ecuación del plano que tenemos,
2(2k + 1) – 2(-2k + 2/3) +4(4k + 2) + 5 = 0
4k + 2 + 4k – 3 + 16k + 8 + 5 = 0
24k = -12
k = -1/2
Entonces, la coordenada del pie de la perpendicular = (0, 5/2, 0)
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
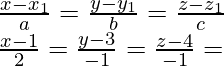
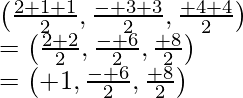
=5\\ [(2+3λ)\hat{i}+(-1+4λ)\hat{j}+(2+12λ)\hat{k}](\hat{i}-\hat{j}+\hat{k})=5\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6a0597c4ecdc7df7c6b78b933605d876_l3.png)