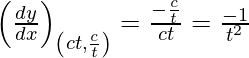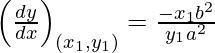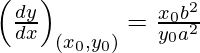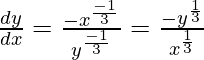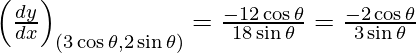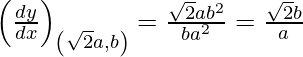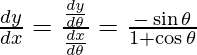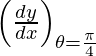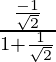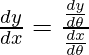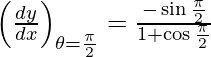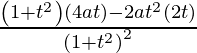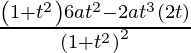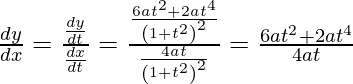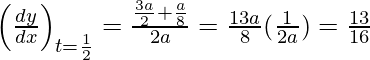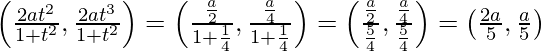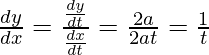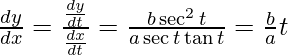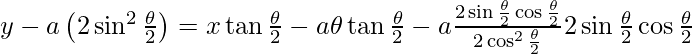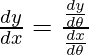Pregunta 1. Encuentra la ecuación de la tangente a la curva √x + √y = a en el punto (a 2/4, a 2/4 ) .
Solución:
Tenemos,
√x + √y = un
Al diferenciar ambos lados de x, obtenemos
dy/dx = -√y/√x
Dado, (x 1 , y 1 ) = (a 2/4 , a 2/4 ),
Pendiente de la tangente, m =
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y – un 2/4 = –1(x – un 2/4 )
y – un 2/4 = –x + un 2/4
x + y = un 2/2
Pregunta 2. Encuentra la ecuación de la normal a y = 2x 3 − x 2 + 3 en (1, 4).
Solución:
Tenemos,
y = 2x 3 − x 2 + 3
Al diferenciar ambos lados de x, obtenemos
dy/dx = 6x 2 – 2x
Pendiente de la tangente =
= 6 (1) 2 – 2 (1) = 4
Pendiente de la normal = – 1/Pendiente de la tangente = – 1/4
Dado, (x 1 , y 1 ) = (1, 4),
La ecuación de la normal es,
y – y 1 = metro (x – x 1 )
y-4 = -1/4 (x-1)
4y – 16 = – x + 1
x + 4y = 17
Pregunta 3. Encuentra la ecuación de la tangente y la normal a la siguiente curva en el punto indicado:
(i) y = x 4 − bx 3 + 13x 2 − 10x + 5 en (0, 5)
Solución:
Tenemos,
y = x 4 − bx 3 + 13x 2 − 10x + 5
Al diferenciar ambos lados de x, obtenemos
dy/dx = 4x 3 – 3bx 2 + 26x – 10
Pendiente de la tangente, m=
= -10
Dado, (x 1 , y 1 ) = (0, 5)
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y – 5 = – 10 (x – 0)
y – 5 = -10x
y + 10x – 5 = 0
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y-5 = 1/10 (x-0)
10 años – 50 = x
x – 10y + 50 = 0
(ii) y = x 4 − 6x 3 + 13x 2 − 10x + 5 en x = 1
Solución:
Tenemos,
y = x 4 − 6x 3 + 13x 2 − 10x + 5
Cuando x = 1, tenemos y = 1 – 6 + 13 – 10 + 5 = 3
Entonces, (x 1 , y 1 ) = (1, 3)
Ahora, y = x 4 − 6x 3 + 13x 2 − 10x + 5
Al diferenciar ambos lados de x, obtenemos
dy/dx = 4 x 3 – 18 x 2 + 26x – 10
Pendiente de la tangente, m =
= 4 – 18 + 26 – 10 = 2
La ecuación de la tangente es,
y-y1 = 2 (x- x1 )
y-3 = 2 (x-1)
y-3 = 2x-2
2x – y + 1 = 0
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y-3 = -1/2 (x-1)
2y – 6 = – x + 1
x + 2y – 7 = 0
(iii) y = x 2 en (0, 0)
Solución:
Tenemos,
y = x2
Al diferenciar ambos lados de x, obtenemos
dy/dx = 2x
Dado, (x 1 , y 1 ) = (0, 0)
Pendiente de la tangente, m=
= 2 (0) = 0
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y-0 = 0 (x-0)
y = 0
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y – 0 = -1/0 (x – 0)
x = 0
(iv) y = 2x 2 − 3x − 1 en (1, −2)
Solución:
Tenemos,
y = 2x 2 − 3x − 1
Al diferenciar ambos lados de x, obtenemos
dy/dx = 4x – 3
Dado, (x 1 , y 1 ) = (1, -2)
Pendiente de la tangente, m =
= 4 – 3 = 1
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y + 2 = 1 (x – 1)
y + 2 = x – 1
x-y-3 = 0
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y + 2 = -1 (x – 1)
y + 2 = -x + 1
x + y + 1 = 0
(v) 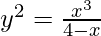 en (2, -2)
en (2, -2)
Solución:
Tenemos,
Al diferenciar ambos lados de x, obtenemos
=
=
Dado, (x 1 , y 1 ) = (2, -2)
Pendiente de la tangente, m=
=
= -2
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y + 2 = -2 (x – 2)
y + 2 = -2x + 4
2x + y – 2 = 0
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y + 2 = 1/2 (x – 2)
2y + 4 = x – 2
x-2y-6 = 0
(vi) y = x 2 + 4x + 1 en x = 3
Solución:
Tenemos,
y = x 2 + 4x + 1
Al derivar ambos lados de x, obtenemos,
dy/dx = 2x + 4
Cuando x = 3, y = 9 + 12 + 1 = 22
Entonces, (x 1 , y 1 ) = (3, 22)
Pendiente de la tangente, m=
= 10
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y-22 = 10 (x-3)
y-22 = 10x-30
10x-y-8 = 0
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y-22 = -1/10 (x-3)
10y – 220 = – x + 3
x + 10y – 223 = 0
(vii) 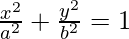 en (a cos θ, b sen θ)
en (a cos θ, b sen θ)
Solución:
Tenemos,
Al diferenciar ambos lados de x, obtenemos
dy/dx = -xb 2 /ya 2
Pendiente de la tangente, m=
Dado, (x 1 , y 1 ) = (a cos θ, b sen θ)
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y – b sen θ = -bcosθ/asinθ (x – a cos θ)
ay sen θ – ab sen 2 θ = -bx cos θ + ab cos 2 θ
bx cos θ + ay sen θ = ab
Al dividir por ab, obtenemos
x/a cosθ + y/b senθ = 1
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y – b sin θ = asinθ/bcosθ (x – a cos θ)
por cos θ – b 2 sen θ cos θ = ax sen θ – a 2 sen θ cos θ
hacha sen θ – by cos θ = (a 2 – b 2 ) sen θ cos θ
Al dividir por sen θ cos θ, obtenemos
hacha sec θ – by cosec θ = a 2 – b 2
(viii) 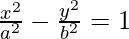 en (a sec θ, b tan θ)
en (a sec θ, b tan θ)
Solución:
Tenemos,
Al diferenciar ambos lados de x, obtenemos
dy/dx = xb 2 /ya 2
Pendiente de la tangente}, m=
Dado, (x 1 , y 1 ) = (a sec θ, b tan θ)
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y – b tan θ =
(x – a sec θ)
ay sen θ – ab(sen 2 θ/cos θ) = bx – (ab/cos θ)
ay sen θ cos θ – ab sen 2 θ = bx cos θ – ab
bx cos θ – ay sen θ cos θ = ab (1 – sen 2 θ)
bx cos θ – ay sen θ cos θ = ab cos 2 θ
Al dividir por ab cos 2 θ, obtenemos
x/a seg θ – y/b tan θ = 1
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y – b tan θ = -a sin θ/b (x – a sec θ)
por – b 2 tan θ = -ax sen θ + a 2 tan θ
hacha sen θ + by = (a 2 + b 2 ) tan θ
Al dividir por tan θ, obtenemos
hacha cos θ + by cot θ = a 2 + b 2
(ix) y 2 = 4ax en (a/m 2 , 2a/m)
Solución:
Tenemos,
y2 = 4ax
Al diferenciar ambos lados de x, obtenemos
dy/dx = 2a/y
Dado, (x 1 , y 1 ) = (a/m 2 , 2a/m)
Pendiente de la tangente =
= m
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
mi – 2a = metro 2 x – un
m 2 x – mi + a = 0
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
metro 3 y – 2a metro 2 = – metro 2 x + un
metro 2 x + metro 3 y – 2a metro 2 – un = 0
(x) c 2 (x 2 + y 2 ) = x 2 y 2 en (c/cos θ, c/sen θ)
Solución:
Tenemos,
do 2 (x 2 + y 2 ) = x 2 y 2
Al diferenciar ambos lados de x, obtenemos
2x c 2 + 2y c 2 (dy/dx) = x 2 2y(dy/dx) + 2x y 2
dy/dx(2y c 2 – 2 x 2 y) = 2x y 2 – 2x c 2
Pendiente de la tangente, m=
=
=
=
= -cos 3 θ/ sen 3 θ
Dado, (x 1 , y 1 ) = (c/cos θ, c/sen θ)
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
sen 2 θ (y sen θ – c) = -cos 2 θ (x cos θ – c)
y sen 3 θ – c sen 2 θ = – x cos 3 θ + c cos 2 θ
x cos 3 θ + y sen 3 θ = c ( sen 2 θ + cos 2 θ)
x cos 3 θ + y sen 3 θ = c
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
sen 3 θ – ycos 3 θ = 2c[-cos (2θ)/sen(2θ)]
sen 3 θ – y cos 3 θ = -2c cot 2θ
sen 3 θ – y cos 3 θ + 2c cot 2θ = 0
(xi) xy = c 2 en (ct, c/t)
Solución:
Tenemos,
xy = c 2
Al diferenciar ambos lados de x, obtenemos
dy/dx = – y/x
Dado, (x 1 , y 1 ) = (ct, c/t)
Pendiente de la tangente, m=
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
yt 2 – ct = -x + ct
x + yt 2 = 2ct
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y – c/t – t 2 (x – ct)
yt – c = t 3 x – ct 4
xt 3 – yt = ct 4 – c
(xii) 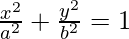 en (x 1 , y 1 )
en (x 1 , y 1 )
Solución:
Tenemos,
Al diferenciar ambos lados de x,
dy/dx = – xb 2 /ya 2
Pendiente de la tangente, m=
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y – y 1 = – x 1 segundo 2 /y 1 un 2 (x – x 1 )
yy 1 un 2 – y 1 2 un 2 = -xx 1 segundo 2 + x 1 2 segundo 2
xx 1 segundo 2 + yy 1 un 2 = X 1 2 segundo 2 + y 1 2 un 2 . . . . (1)
Dado que (x 1 , y 1 ) se encuentra en la curva, obtenemos
X 1 2 segundo 2 + y 1 2 un 2 = un 2 segundo 2
Sustituyendo esto en (1), obtenemos
xx 1 segundo 2 + yy 1 un 2 = un 2 segundo 2
Al dividir esto por a 2 b 2 , obtenemos
La ecuación de la normal es,
y – y 1 = metro (x – x 1 )
y – y 1 = y 1 un 2 /x 1 segundo 2 (x – x 1 )
yx 1 segundo 2 – x 1 y 1 segundo 2 = xy 1 un 2 – x 1 y 1 un 2
xy 1 un 2 – yx 1 segundo 2 = x 1 y 1 un 2 – x 1 y 1 segundo 2
xy 1 a 2 – yx 1 b 2 = x 1 y 1 (a 2 – b 2 )
Al dividir por x 1 y 1 , obtenemos
(xiii) 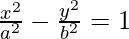 en (x 0 , y 0 )
en (x 0 , y 0 )
Solución:
Tenemos,
Al diferenciar ambos lados de x, obtenemos
dy/dx = xb 2 /ya 2
Pendiente de la tangente, m=
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y – y 0 = x 0 segundo 2 / y 0 un 2 (x – x 0 )
yy 0 un 2 – y 0 2 un 2 = xx 0 segundo 2 – x 0 2 segundo 2
xx 0 segundo 2 – yy 0 un 2 = X 0 2 segundo 2 – y 0 2 un 2 . . . . (1)
x 0 2 segundo 2 – y 0 2 un 2 = un 2 segundo 2
Sustituyendo esto en la ecuación (1), obtenemos,
xx 0 segundo 2 – yy 0 un 2 = un 2 segundo 2
Dividiendo esto por a 2 b 2 , obtenemos
La ecuación de la normal es,
y – y 1 = metro (x – x 1 )
y – y 0 = y 0 un 2 /x 0 segundo 2 (x – x 0 )
yx 0 segundo 2 – x 0 y 0 segundo 2 = -xy 0 un 2 + x 0 y 0 un 2
xy 0 un 2 + yx 0 segundo 2 = x 0 y 0 un 2 + x 0 y 0 segundo 2
xy 0 un 2 + yx 0 segundo 2 = x 0 y 0 (un 2 + segundo 2 )
Dividiendo por x 0 y 0 , obtenemos
(xiv) 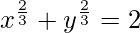 en (1, 1)
en (1, 1)
Solución:
Tenemos,
Al diferenciar ambos lados de x, obtenemos
Pendiente de la tangente, m=
= -1
Dado, (x 1 , y 1 ) = (1, 1)
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y-1 = -1 (x-1)
y – 1 = -x + 1
x + y – 2 = 0
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y-1 = 1 (x-1)
y-1 = x-1
y-x = 0
(xv) x 2 = 4y en (2, 1)
Solución:
Tenemos,
x2 = 4y
Al diferenciar ambos lados de x, obtenemos
2x = 4dy/dx
dy/dx = x/2
Pendiente de la tangente, m=
= 2/2 = 1
Dado, (x 1 , y 1 ) = (2, 1)
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y-1 = 1 (x-2)
y-1 = x-2
x-y-1 = 0
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y – 1 = – 1 (x – 2)
y – 1 = – x + 2
x + y – 3 = 0
(xvi) y 2 = 4x en (1, 2)
Solución:
Tenemos,
y2 = 4x
Al diferenciar ambos lados de x, obtenemos
2y (dy/dx) = 4
dy/dx = 2/año
Pendiente de la tangente, m=
= 2/2 = 1
Dado, (x 1 , y 1 ) = (1, 2)
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y-2 = 1 (x-1)
y-2 = x-1
x – y + 1 = 0
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y-2 = -1 (x-1)
y – 2 = -x + 1
x + y – 3 = 0
(xvii) 4x 2 + 9y 2 = 36 en (3 cos θ, 2 sen θ)
Solución:
Tenemos,
4x 2 + 9y 2 = 36
Al diferenciar ambos lados de x, obtenemos
8x + 18y dy/dx = 0
18y dy/dx = – 8x
dy/dx = -8x/18y = -4x/9y
Pendiente de la tangente, m =
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y – 2 sen θ = -2 cos θ/3 sen θ(x – 3 cos θ)
3y sen θ – 6 sen 2 θ = -2x cos θ + 6 cos 2 θ
2x cos θ + 3y sen θ = 6 (cos 2 θ + sen 2 θ)
2x cos θ + 3y sen θ = 6
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y – 2 sen θ = -3 sen θ/2 cos θ(x – 3 cos θ)
2y cos θ – 4 sen θ cos θ = 3x sen θ – 9 sen θ cos θ
3x sen θ – 2y cos θ – 5 sen θ cos θ = 0
(xviii) y 2 = 4ax en (x 1 , y 1 )
Solución:
Tenemos,
y2 = 4ax
Al diferenciar ambos lados de x, obtenemos
2y dy/dx = 4a
dy/dx = 2a/y
En (x 1 , y 1 ), tenemos
Pendiente de la tangente =
= m
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
yy 1 – y 1 2 = 2ax – 2a x 1
yy 1 – 4a x 1 = 2ax – 2a x 1
yy 1 = 2ax + 2a x 1
yy1 = 2a (x + x1 )
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y – y 1 = -y 1 /2a (x – x 1 )
(xix) 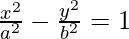 en (√2a, b)
en (√2a, b)
Solución:
Tenemos,
Al diferenciar ambos lados de x, obtenemos
dy/dx = xb 2 /ya 2
Pendiente de la tangente, m=
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y – b = √2b/a(x – √2a)
ay – ab = √2 bx – 2ab
√2 bx – ay = ab
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y – b = – a/√2b(x – √2a)
√2 por – √2 segundo 2 = – hacha + √2 un 2
hacha + √2 por = √2 segundo 2 + √2 un 2
hacha/√2 + por = a 2 + b 2
Pregunta 4. Encuentra la ecuación de la tangente a la curva x = θ + sen θ, y = 1 + cos θ en θ = π/4.
Solución:
Tenemos,
x = θ + sen θ, y = 1 + cos θ
y
Pendiente de la tangente, m =
=
=
=
=
= 1 – √2
Dado, (x 1 , y 1 ) = (π/4 + sen π/4, 1 + cos π/4) = (π/4 + 1/√2, 1 + 1/√2)
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y – (1 + 1/√2) = (1 – √2) [x – (π/4 + 1/√2)]
y – 1 – 1/√2 = (1 – √2) (x – π/4 – 1/√2)
Pregunta 5. Encuentra la ecuación de la tangente y la normal a la siguiente curva en los puntos indicados.
(i) x = θ + sen θ, y = 1 + cos θ en θ = π/2
Solución:
Tenemos,
x = θ + sen θ y y = 1 + cos θ
dx/dθ = 1 + cos θ y dy/dθ = -sinθ
=
Pendiente de la tangente, m=
= -1/(1 + 0)
= -1
Dado, (x 1 , y 1 ) = (π/2 + sen π/2, 1 + cos π/2) = (π/2 + 1, 1)
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y – 1 = -1 (x – π/2 – 1)
2y – 2 = – 2x + π + 2
x + 2y – π – 4 = 0
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y – 1 = 1 (x – π/2 -1)
2y – 2 = 2x – π – 2
2x – 2y = π
(ii) 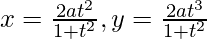 en t = 1/2
en t = 1/2
Solución:
Tenemos,
dx/dt =
=
dy/dt =
=
Pendiente de la tangente, m=
Dado, (x 1 , y 1 ) =
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
80y – 16a = 65x – 26a
65x – 80y – 10a = 0
13x – 16y – 2a = 0
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
65y – 13a = – 80x + 32a
80x + 65y – 45a = 0
16x + 13y – 9a = 0
(iii) x = en 2 , y = 2 en t = 1
Solución:
Tenemos,
x = en 2 , y = 2 en
dx/dt = 2at y dy/dt = 2a
Pendiente de la tangente, m=
= 1
Dado, (x 1 , y 1 ) = (a, 2a)
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y – 2a = 1 (x – a)
y-2a = x-a
x – y + a = 0
Ecuación de la normalidad:
y – y 1 = -1/m (x – x 1 )
y – 2a = – 1 (x – a)
y – 2a = – x + un
x + y = 3a
(iv) x = un segundo t, y = b tan t en t
Solución:
Tenemos,
x = un segundo t, y = segundo tan t
dx/dt = a sect tant y dy/dt = b sec 2 t
Pendiente de la tangente, m =
Dado (x 1 , y 1 ) = (a sec t, b tan t)
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y – b tan t = (b/a) cosec t (x – a sec t)
ay sen t cos t – ab sen 2 t = bx cos t – ab
bx cos t – ay sen t cos t – ab (1 – sen 2 t) = 0
bx cos t – ay sen t cos t = ab cos 2 t
Al dividir por cos 2 t, obtenemos
bx seg t – ay tan t = ab
La ecuación de la normal es,
y – y 1 = -1/m (x – x 1 )
y – b tant = -a/b sint(x – asect)
por cos t – b 2 sen t = – ax sen t cos t + a 2 sen t
hacha sen t cos t + by cos t = (a 2 + b 2 ) sen t
Al dividir ambos lados por sen t, obtenemos
hacha cos t + por cuna t = a 2 + b 2
(v) x = a(θ + sen θ), y = a(1 − cos θ) en θ
Solución:
Tenemos,
x = a(θ + sen θ), y = a(1 − cos θ)
dx/dθ = a(1 + cosθ) y dy/dθ = asinθ
=
=
=
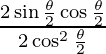
= bronceado θ/2 . . . . (1)
Pendiente de la tangente, m=
Dado (x 1 , y 1 ) = [a(θ + sin θ), a(1 − cos θ)]
La ecuación de la tangente es,
y – y 1 = metro (x – x 1 )
y – a (1 – cos θ) = tan θ/2 [x – a (θ + sen θ)]
y − 2asen 2 θ/2 =(x − aθ)tan θ/2 − 2asen 2
y = (x – aθ) tan θ/2
La ecuación de la normal es,
y – a (1 – cos θ) = -cot θ/2 [x – a (θ + sen θ)]
tan θ/2 (y – 2a) + a (2sen θ/2 cosθ/2 = -x + aθ + a senθ
tan θ/2 (y – 2a) + a sen θ = -x + aθ + a sen θ
tan θ/2 (y – 2a) = – x + aθ
tan θ/2 (y – 2a) + x – θ = 0
(vi) x = 3 cos θ − cos 3 θ, y = 3 sen θ − sen 3 θ
Solución:
Tenemos,
x = 3 cos θ − cos 3 θ, y = 3 sen θ − sen 3 θ
dx/dθ = -3sen θ + 3 cos 2 θ sen θ y dy/dθ = 3 cos θ – 3 sen 2 θ cos θ
=
=
= cos 3 θ/ -sen 3 θ
= tan 3 θ
Entonces la ecuación de la tangente en θ es,
y – 3 sen θ + sen 3 θ = -tan 3 θ (x – 3 cos θ + cos 3 θ)
4 (y cos 3 θ – x sen 3 θ) = 3 sen 4θ
Entonces la ecuación de normal en θ es,
y – 3 sen θ + sen 3 θ= (1/tan 3 θ) (x – 3 cos θ + cos 3 θ)
sen 3 θ – x cos 3 θ = 3 sen 4 θ – sen 6 θ – 3 cos 4 θ + cos 6 θ
Pregunta 6. ¿Encontrar la ecuación de la normal a la curva x 2 + 2y 2 − 4x − 6y + 8 = 0 en el punto cuya abscisa es 2?
Solución:
Dado que la abscisa = 2, es decir, x = 2
X 2 + 2y 2 – 4x – 6y + 8 = 0 . . . . (1)
Al diferenciar ambos lados de x, obtenemos
2x + 4y dy/dx – 4 – 6 dy/dx = 0
dy/dx(4y – 6) = 4 – 2x
Cuando x = 2, obtenemos
4 + 2y 2 – 8 – 6y + 8 = 0
2 años 2 – 6 años + 4 = 0
y 2 – 3y + 2 = 0
y = 2 o y = 1
m (tangente) en x = 2 es 0
Normal es perpendicular a la tangente entonces, m 1 m 2 = –1
m (normal) en x = 2 es 1/0, que no está definido.
La ecuación de lo normal viene dada por y – y 1 = m (normal) (x – x 1 )
x = 2
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
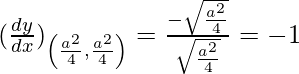
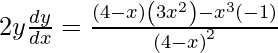
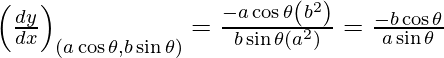
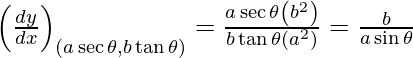
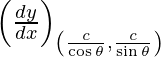
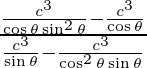
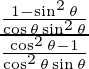
![Rendered by QuickLaTeX.com x \sin^3 \theta - y \cos^3 \theta = c\left[ \frac{\left( \sin^2 \theta + \cos^2 \theta \right)\left( \sin^2 \theta - \cos^2 \theta \right)}{\cos\theta \sin\theta} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e0be6ba0e0a40439800980bff7b09216_l3.png)
![Rendered by QuickLaTeX.com \sin^3 \theta - y \cos^3 \theta =2c \left[ \frac{- \left( \cos^2 \theta - \sin^2 \theta \right)}{2\cos\theta \sin\theta} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3a6ecbbacf92987bf95bf7652d1978d1_l3.png)