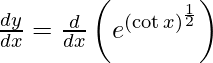Pregunta 1. Diferenciar y = sen (3x + 5) con respecto a x.
Solución:
Tenemos,
y = sen (3x + 5)
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Pregunta 2. Diferenciar y = tan 2 x con respecto a x.
Solución:
Tenemos,
y = bronceado 2 x
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Pregunta 3. Diferenciar y = tan (x + 45°) con respecto a x.
Solución:
Tenemos,
y = bronceado (x + 45°)
y =
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Pregunta 4. Diferenciar y = sen (log x) con respecto a x.
Solución:
Tenemos,
y = sen (log x)
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Pregunta 5. Diferenciar y = e sen √x con respecto a x.
Solución:
Tenemos,
y = e sen √x
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Al usar de nuevo la regla de la string, tenemos
Pregunta 6. Diferenciar y = e tan x con respecto a x.
Solución:
Tenemos,
y = e tan x
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Pregunta 7. Diferenciar y = sen 2 (2x + 1) con respecto a x.
Solución:
Tenemos,
y = sen 2 (2x + 1)
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Al usar de nuevo la regla de la string, tenemos
Como sen 2A = 2 sen A cos A, obtenemos
Pregunta 8. Derive y = log 7 (2x − 3) con respecto a x.
Solución:
Tenemos,
y = registro 7 (2x − 3)
Como
, tenemos
y =
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Pregunta 9. Diferenciar y = tan 5x° con respecto a x.
Solución:
Tenemos,
y = tan 5x°
y =
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Pregunta 10. Deriva y = 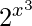 con respecto a x.
con respecto a x.
Solución:
Tenemos,
y =
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Pregunta 11. Deriva y = 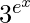 con respecto a x.
con respecto a x.
Solución:
Tenemos,
y =
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Pregunta 12. Diferenciar y = log x 3 con respecto a x.
Solución:
Tenemos,
y = logaritmo x 3
como
, obtenemos
y =
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
como
, obtenemos
Pregunta 13. Deriva y = 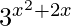 con respecto a x.
con respecto a x.
Solución:
Tenemos,
y =
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Pregunta 14. Diferenciar y = 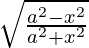 con respecto a x.
con respecto a x.
Solución:
Tenemos,
y =
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Pregunta 15. Deriva y = 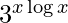 con respecto a x.
con respecto a x.
Solución:
Tenemos,
y =
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Pregunta 16. Deriva y = 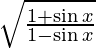 con respecto a x.
con respecto a x.
Solución:
Tenemos,
y =
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Pregunta 17. Deriva y = 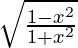 con respecto a x.
con respecto a x.
Solución:
Tenemos,
y =
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Pregunta 18. Diferenciar y = (log sen x) 2 con respecto a x.
Solución:
Tenemos,
y = (log sen x) 2
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Pregunta 19. Deriva y = 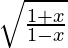 con respecto a x.
con respecto a x.
Solución:
Tenemos,
y =
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Al usar la regla del cociente, tenemos
Pregunta 20. Deriva y = 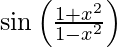 con respecto a x.
con respecto a x.
Solución:
Tenemos,
y =
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Al usar la regla del cociente, tenemos
Pregunta 21. Deriva y = 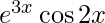 con respecto a x.
con respecto a x.
Solución:
Tenemos,
y =
Al diferenciar y con respecto a x obtenemos,
Al usar la regla del producto, tenemos
Al usar la regla de la string, tenemos
Pregunta 22. Diferenciar y = sin(log sin x) con respecto a x.
Solución:
Tenemos,
y = sen(log sen x)
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Al usar de nuevo la regla de la string, tenemos
Pregunta 23. Diferenciar y = e tan 3x con respecto a x.
Solución:
Tenemos,
y = e tan 3x
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Pregunta 24. Deriva y = 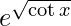 con respecto a x.
con respecto a x.
Solución:
Tenemos,
y =
Al diferenciar y con respecto a x obtenemos,
Al usar la regla de la string, tenemos
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
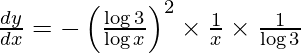
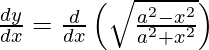
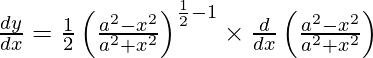
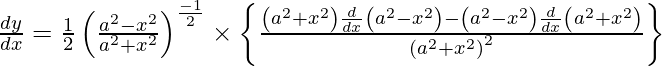

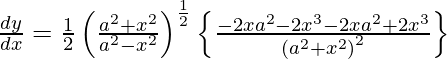
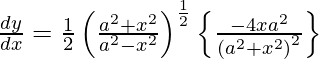
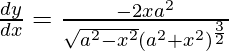
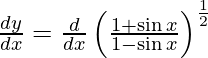
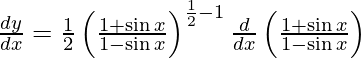
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{1}{2} \left( \frac{1 - \sin x}{1 + \sin x} \right)^\frac{1}{2} \left[ \frac{\left( 1 - \sin x \right)\left( \cos x \right) - \left( 1 + \sin x \right)\left( - \cos x \right)}{\left( 1 - \sin x \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d0af64861031fc2e10422b97e18b2666_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{1}{2}\frac{\left( 1 - \sin x \right)^\frac{1}{2}}{\left( 1 + \sin x \right)^\frac{1}{2}}\left[ \frac{\cos x - \cos x \sin x + \cos x + \sin x \cos x}{\left( 1 - \sin x \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6218bdc45f7de235481ff679392a16a7_l3.png)
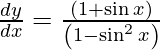
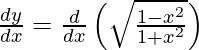
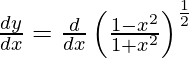
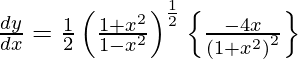

![Rendered by QuickLaTeX.com \frac{d y}{d x} = \cos x\left( \frac{1 + x^2}{1 - x^2} \right)\left[ \frac{\left( 1 - x^2 \right)\frac{d}{dx}\left( 1 + x^2 \right) - \left( 1 + x^2 \right)\frac{d}{dx}\left( 1 - x^2 \right)}{\left( 1 - x^2 \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bddedfb63b1c94b8675018ba115fda60_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \cos x\left( \frac{1 + x^2}{1 - x^2} \right)\left[ \frac{\left( 1 - x^2 \right)\left( 2x \right) - \left( 1 + x^2 \right)\left( - 2x \right)}{\left( 1 - x^2 \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b95a0dbad805cafbcbe2b162be7ef69e_l3.png)