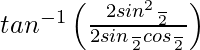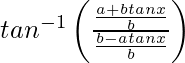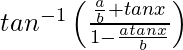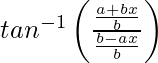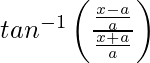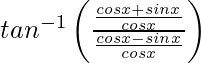Pregunta 17. Deriva 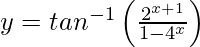 , −∞ < x < 0 con respecto a x.
, −∞ < x < 0 con respecto a x.
Solución:
Tenemos,
, −∞ < x < 0
Al poner 2 x = tan θ, obtenemos,
=
Ahora, −∞ < x < 0
=> 0 < 2 x < 1
=> 0 < θ < π/4
=> 0 < 2θ < π/2
Entonces, y = 2θ
= 2 tan −1 (2 x )
Derivando con respecto a x, obtenemos,
=
=
Pregunta 18. Diferenciar 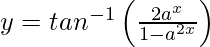 , a > 1, −∞ < x < 0 con respecto a x.
, a > 1, −∞ < x < 0 con respecto a x.
Solución:
Tenemos,
, −∞ < x < 0
Al poner a x = tan θ, obtenemos,
=
Ahora, −∞ < x < 0
=> 0 < un x < 1
=> 0 < θ < π/4
=> 0 < 2θ < π/2
Entonces, y = 2θ
= 2 tan −1 ( ax )
Derivando con respecto a x, obtenemos,
=
=
Pregunta 19. Diferenciar 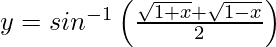 , 0 < x < 1 con respecto a x.
, 0 < x < 1 con respecto a x.
Solución:
Tenemos,
, 0 < x < 1
Al poner x = cos 2θ, obtenemos,
=
=
=
=
Ahora, 0 < x < 1
=> 0 < cos 2θ < 1
=> 0 < 2θ < π/2
=> 0 < θ < π/4
=> π/4 < (θ+π/4) < π/2
Entonces, y =
=
Derivando con respecto a x, obtenemos,
=
=
Pregunta 20. Diferenciar 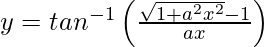 , x ≠ 0 con respecto a x.
, x ≠ 0 con respecto a x.
Solución:
Tenemos,
Al poner ax = tan θ, obtenemos,
=
=
=
=
=
=
Derivando con respecto a x, obtenemos,
=
Pregunta 21. Diferenciar 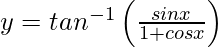 , −π < x < π con respecto a x.
, −π < x < π con respecto a x.
Solución:
Tenemos,
, −π < x < π
=
=
=
Derivando con respecto a x, obtenemos,
=
Pregunta 22. Diferenciar 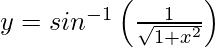 con respecto a x.
con respecto a x.
Solución:
Tenemos,
Al poner x = cot θ, obtenemos,
=
=
= θ
= cuna −1 x
Derivando con respecto a x, obtenemos,
=
Pregunta 23. Diferenciar 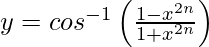 , 0 < x < ∞ con respecto a x.
, 0 < x < ∞ con respecto a x.
Solución:
Tenemos,
,0 < x < ∞
Al poner x n = tan θ, obtenemos,
=
Ahora, 0 < x < ∞
=> 0 < X norte < ∞
=> 0 < θ < π/2
=> 0 < 2θ < π
Entonces, y = 2θ
= 2 tan –1 (x n )
Derivando con respecto a x, obtenemos,
=
=
Pregunta 24. Derive 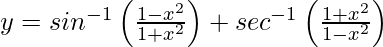 , x ∈ R con respecto a x.
, x ∈ R con respecto a x.
Solución:
Tenemos,
=
=
Derivando con respecto a x, obtenemos,
= 0
Pregunta 25. Diferenciar 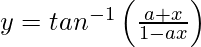 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=
Derivando con respecto a x, obtenemos,
= 0 +
=
Pregunta 26. Diferenciar 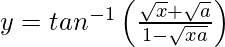 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=
Derivando con respecto a x, obtenemos,
=
=
Pregunta 27. Diferenciar 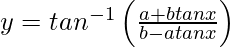 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=
=
=
=
Derivando con respecto a x, obtenemos,
= 0 + 1
= 1
Pregunta 28. Diferenciar 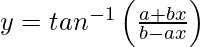 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=
=
=
Derivando con respecto a x, obtenemos,
= 0 +
=
Pregunta 29. Diferenciar 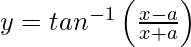 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=
=
=
Derivando con respecto a x, obtenemos,
=
=
=
Pregunta 30. Diferenciar 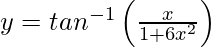 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=
=
Derivando con respecto a x, obtenemos,
=
=
Pregunta 31. Diferenciar 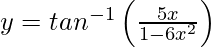 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=
=
Derivando con respecto a x, obtenemos,
=
=
Pregunta 32. Diferenciar 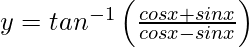 , −π/4 < x < π/4 con respecto a x.
, −π/4 < x < π/4 con respecto a x.
Solución:
Tenemos,
, −π/4 < x < π/4
=
=
=
=
=
Derivando con respecto a x, obtenemos,
= 0 + 1
= 1
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA