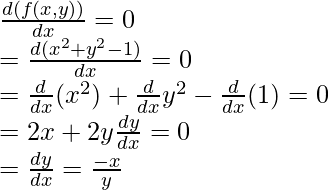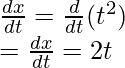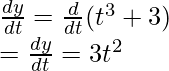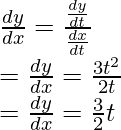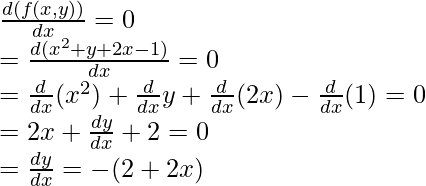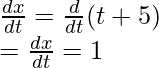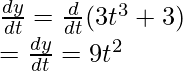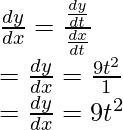Los derivados se utilizan para medir la tasa de cambio de cualquier cantidad. Este proceso se llama diferenciación. Se puede considerar como un bloque de construcción de la teoría del cálculo. Hablando geométricamente, la derivada de cualquier función en un punto particular da la pendiente de la tangente en ese punto de la función. Hay muchos métodos para resolver y calcular las derivadas de las funciones. La forma habitual es calcular a través de la regla de la string y la regla de la potencia. En algunos casos, las funciones se vuelven demasiado complejas para calcular. En tales casos, hay ciertos métodos que deben seguirse para facilitar los cálculos.
Derivados
Los derivados se definen como la tasa de cambio de alguna variable/cantidad que se observa. Supongamos que la variable o la cantidad se rige por la ecuación f(x). La derivada de esta función se denota por ![]() o F(x). Hay ciertas funciones cuyas derivadas deben tenerse en cuenta. Estas funciones ayudan a simplificar el cálculo de las derivadas. La siguiente tabla muestra las derivadas de algunas funciones estándar.
o F(x). Hay ciertas funciones cuyas derivadas deben tenerse en cuenta. Estas funciones ayudan a simplificar el cálculo de las derivadas. La siguiente tabla muestra las derivadas de algunas funciones estándar.
| Función | Derivado |
| pecado(x) | porque(x) |
| porque(x) | -sin(x) |
| x norte | nx n-1 |
| bronceado(x) | segundo 2 (x) |
| cuna(x) | cosec 2 (x) |
A veces, las funciones se componen de productos o división de dos o más funciones. En tales casos, se utiliza la regla del producto y el cociente. Considere una función h(x),
Regla del producto: Ifh(x) = f(x).g(x)
h'(x) = f'(x)g(x) + f(x)g'(x)
Regla del cociente: Ifh(x) = f(x)/g(x)
String de reglas
A menudo, las funciones se componen de una composición de dos o más funciones estándar. En tales casos, las técnicas usuales para encontrar las derivadas no son suficientes. En ese caso, la regla de la string viene al rescate. Considere f(x) y g(x) como dos funciones diferenciables, asumiendo que forman una nueva función h(x) = f(g(x)), que es básicamente una composición de estas funciones. En este caso, la regla de la string se puede aplicar como se menciona a continuación,
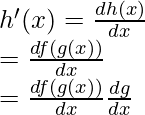
Diferenciación Avanzada
Hay algunas funciones para las que calcular la derivada no es fácil. Requiere cierta manipulación algebraica antes de calcular sus derivadas. Ejemplos de tales funciones son funciones implícitas, funciones paramétricas, derivadas de orden superior y derivadas logarítmicas. Todas estas funciones se componen de funciones estándar, pero son muy complejas de resolver mediante la regla de la string simple o regla de la potencia.
Derivadas de funciones implícitas
Las funciones implícitas son las funciones que tienen la forma f(x, y) = 0. Las funciones habituales que se encuentran tienen la forma y = f(x). Estas funciones son funciones explícitas porque la definición de y se expresa claramente y se expresa en términos de x. En funciones implícitas, la relación entre x e y no está completamente clara. Veamos este método como ejemplo.
Pregunta: Encuentra la derivada de la función x 2 + y 2 = 4.
Responder:
Observe que la función dada es una función implícita,
x2 + y2 = 4
⇒ x2 + y2 – 4 = 0
Esta función tiene la forma de f(x, y) = 0.
Derivadas de funciones paramétricas
En las funciones estudiadas anteriormente, las funciones tenían solo dos variables y se definió una relación entre ellas. A menudo, en algunas funciones, la relación entre dos variables se describe utilizando una tercera variable. Estas funciones se llaman funciones paramétricas. Por ejemplo, x = f(t) y y = g(t) en una de esas funciones. En esta función, las variables x e y se definen con respecto a la variable “t”. En este caso, calcular la tasa de cambio de x con respecto a y no es tan claro.
Pregunta: Calcula la derivada de la siguiente función.
x = t 2 y y = t 3 + 3.
Responder:
Este es un ejemplo de una función paramétrica. En este caso, las derivadas se calculan con respecto a la tercera variable para ambas funciones.
x = t 2
Diferenciando con respecto a “t”,
Ahora bien, estos derivados se pueden combinar.
Derivadas de orden superior
Al igual que las derivadas se definen como la tasa de cambio de una cantidad. De manera similar, también se puede calcular la tasa de cambio de la tasa de cambio. Tales derivados que miden la tasa de cambio de un derivado se denominan derivados de orden superior. Por ejemplo, la tasa de cambio de posición viene dada por la velocidad, y la aceleración mide la tasa de cambio de velocidad. Para la función f(x),
![]() denotes a first-order derivative. Similarly,
denotes a first-order derivative. Similarly, ![]() denotes the second-order derivative and so on.
denotes the second-order derivative and so on.
Problemas de muestra
Pregunta 1: Encuentra el segundo orden de la derivada de f(x) = x 3 .
Responder:
La derivada de primer orden de esta función viene dada por,
f(x) = x3
⇒ f'(x) = 3x 2
Derivando de nuevo la función,
f”(x) = 6x
Pregunta 2: Encuentra la derivada de la función dada,
f(x) = sen(x)cos(x)
Respuesta :
Dado: f(x) = sin(x)cos(x)
La función dada es el producto de dos funciones, por lo que se debe aplicar la regla del producto.
f(x) = h(x)g(x)
⇒f'(x) = h'(x)g(x) + h(x)g'(x)
Aquí, h(x) = sin(x) y g(x) = cos(x)
f'(x) = h'(x)g(x) + h(x)g'(x)
⇒ f'(x) =
⇒f'(x) =
Pregunta 3: Encuentra la derivada de la función dada,
f(x) = xsen(x)
Respuesta :
Dado: f(x) = xcos(x)
La función dada es el producto de dos funciones, por lo que se debe aplicar la regla del producto.
f(x) = h(x)g(x)
⇒f'(x) = h'(x)g(x) + h(x)g'(x)
Aquí, h(x) = x y g(x) = sin(x)
f'(x) = h'(x)g(x) + h(x)g'(x)
⇒ f'(x) =
⇒f'(x) = sen(x) + xcos(x)
Pregunta 4: Encuentra la derivada de la función x 2 + 2x + y = 1.
Responder:
Observe que la función dada es una función implícita,
x2 + 2x + y = 1.
⇒ x2 + 2x + y – 1 = 0
Esta función tiene la forma de f(x, y) = 0.
Pregunta 5: Calcula la derivada de la siguiente función.
x = t + 5 y y = 3t 3 + 6.
Responder:
Este es un ejemplo de una función paramétrica. En este caso, las derivadas se calculan con respecto a la tercera variable para ambas funciones.
x = t + 5
Diferenciando con respecto a “t”,
Ahora bien, estos derivados se pueden combinar.
Pregunta 6: Encuentra el tercer orden de la derivada de f(x) = e x + sin(x).
Responder:
La derivada de primer orden de esta función viene dada por,
f(x) = e x + sin(x)
⇒ f'(x) = e x + cos(x)
Derivando de nuevo la función,
f”(x) = e x – sen(x)
Derivando de nuevo la función,
f”'(x) = e x – sen(x)
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA