Pregunta 33. Diferenciar 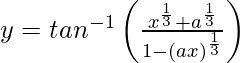 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=
Derivando con respecto a x, obtenemos,
=
=
=
Pregunta 34. Diferenciar  con respecto a x.
con respecto a x.
Solución:
Tenemos,
Al poner 2 x = tan θ, obtenemos,
=
=
=
=
=
=
=
= 2θ
= 2 tan −1 (2 x )
Derivando con respecto a x, obtenemos,
=
=
Pregunta 35. Si 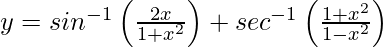 , 0 < x < 1, demuestre que
, 0 < x < 1, demuestre que 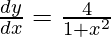 .
.
Solución:
Tenemos,
=
Al poner x = tan θ, obtenemos,
y =
=
=
=
=
=
Ahora, 0 < x < 1
=> 0 < bronceado θ < 1
=> 0 < θ < π/4
=> 0 < 2θ < π/2
Entonces, y = 2θ + 2θ
= 4θ
= 4 tan −1 x
Ahora, LHS =
=
= lado derecho
Por lo tanto probado.
Pregunta 36. Si 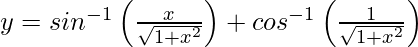 , 0 < x < ∞, demuestre que
, 0 < x < ∞, demuestre que 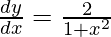 .
.
Solución:
Tenemos,
Al poner x = tan θ, obtenemos,
=
=
=
=
Ahora, 0 < x < ∞
=> 0 < tan θ < ∞
=> 0 < θ < π/2
Entonces, y = θ + θ
= 2θ
= 2 tan −1 x
Ahora, LHS =
=
= lado derecho
Por lo tanto probado.
Pregunta 37 Diferencie lo siguiente con respecto a x :
(i) cos −1 (sen x)
Solución:
Tenemos, y = cos −1 (sen x)
=
=
Derivando con respecto a x, obtenemos,
= 0 − 1
= −1
(ii) 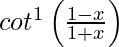
Solución:
Tenemos, y =
Al poner x = tan θ, obtenemos,
=
=
=
=
=
=
Derivando con respecto a x, obtenemos,
= 0 +
=
Pregunta 38. Diferenciar ![Rendered by QuickLaTeX.com y=cot^{-1}\left[\frac{\sqrt{1+sinx}+\sqrt{1-sinx}}{\sqrt{1+sinx}-\sqrt{1-sinx}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9015b75f6699eacdbfd989ff26cc9c13_l3.png) , 0 < x < π /2 con respecto a x.
, 0 < x < π /2 con respecto a x.
Solución:
Tenemos,
=
=
=
=
=
=
=
=
Derivando con respecto a x, obtenemos,
=
Pregunta 39. Si 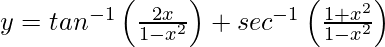 , x > 0, demuestre que
, x > 0, demuestre que 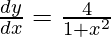 .
.
Solución:
Tenemos,
=
Al poner x = tan θ, obtenemos,
y =
=
=
=
=
=
=
=
=
Aquí, 0 < x < ∞
=> 0 < tan θ < ∞
=> 0 < θ < π/2
=> 0 < 2θ < π
Entonces, y = 2θ + 2θ
= 4θ
= 4 tan −1 x
Ahora, LHS =
=
= lado derecho
Por lo tanto probado.
Pregunta 40. Si  , x > 0, encuentra
, x > 0, encuentra  .
.
Solución:
Tenemos,
=
=
Derivando con respecto a x, obtenemos,
= 0
Pregunta 41. Si ![Rendered by QuickLaTeX.com y=sin\left[2tan^{-1}\sqrt{(\frac{1-x}{1+x})}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bb6ed5ceb9104cb290498f06714f900a_l3.png) , encuentra
, encuentra  .
.
Solución:
Tenemos,
Al poner x = cos 2θ, obtenemos,
=
=
=
=
=
=
=
=
Derivando con respecto a x, obtenemos,
=
=
Pregunta 42. Si 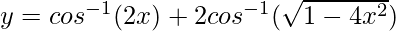 , 0 < x < 1/2, encuentre
, 0 < x < 1/2, encuentre  .
.
Solución:
Tenemos,
Al poner 2x = cos θ, obtenemos,
=
=
Ahora, 0 < x < 1/2
=> 0 < 2x < 1
=> 0 < cos θ < 1
=> 0 < θ < π/2
y 0 > −θ > −π/2
=> π/2 > (π/2 −θ) > 0
Entonces, y =
= π − θ
= π − cos −1 (2x)
Derivando con respecto a x, obtenemos,
=
=
Pregunta 43. Si la derivada de tan −1 (a + bx) toma el valor de 1 en x = 0, demuestre que 1 + a 2 = b.
Solución:
Tenemos, y = tan −1 (a + bx)
Derivando con respecto a x, obtenemos,
=
En x = 0, tenemos,
=>
= 1
=>
= 1
=> 1 + un 2 = segundo
Por lo tanto probado.
Pregunta 44. Si 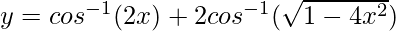 , −1/2 < x < 0, encuentra
, −1/2 < x < 0, encuentra  .
.
Solución:
Tenemos,
Al poner 2x = cos θ, obtenemos,
=
=
Ahora, −1/2 < x < 0
=> −1 < 2x < 0
=> −1 < cos θ < 0
=> π/2 < θ < π
y −π/2 > −θ > −π
=> 0 > (π/2 −θ) > −π/2
Entonces, y =
= −π + 3θ
= −π + 3 porque −1 (2x)
Derivando con respecto a x, obtenemos,
= 0 +
=
Pregunta 45. Si 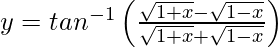 , encuentra
, encuentra  .
.
Solución:
Tenemos,
Al poner x = cos 2θ, obtenemos,
=
=
=
=
=
=
=
=
Derivando con respecto a x, obtenemos,
= 0 –
=
Pregunta 46. Si 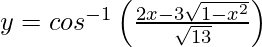 , encuentra
, encuentra .
.
Solución:
Tenemos,
Al poner x = cos θ, obtenemos,
=
=
Dejar
=> sen Ø =
=> sen Ø =
=> sen Ø =
=> sen Ø =
=> sen Ø =
Entonces, y =
=
= Ø + θ
=
Derivando con respecto a x, obtenemos,
= 0 +
=
Pregunta 47. Diferenciar ![Rendered by QuickLaTeX.com y=sin^{-1}\left[\frac{2^{x+1}×3^x}{1+(36)^x}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b8746d78a8494be45d3ac06c2f1e906a_l3.png) con respecto a x.
con respecto a x.
Solución:
Tenemos,
=
=
Al poner 6 x = tan θ, obtenemos,
=
=
=
=
=
=
=
= 2θ
= 2 tan −1 (6 x )
Derivando con respecto a x, obtenemos,
=
=
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
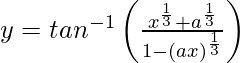
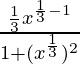
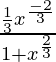
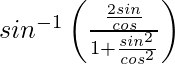
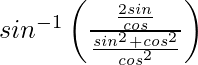
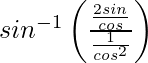
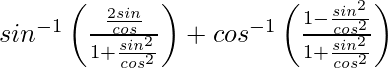

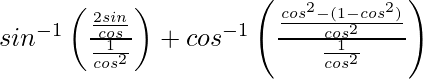

![Rendered by QuickLaTeX.com cot^{-1}\left[\frac{2cos^2\frac{x}{2}}{2sin\frac{x}{2}cos\frac{x}{2}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-af4eec886c5c4caaae06798e0e77ad4c_l3.png)

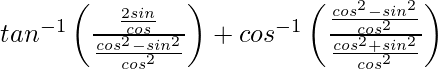
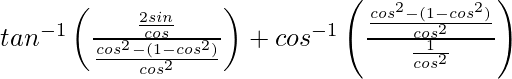
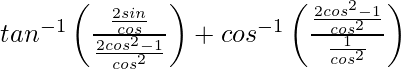
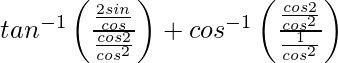
![Rendered by QuickLaTeX.com sin\left[2tan^{-1}\sqrt{(\frac{2sin^2θ}{2cos^2θ})}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-386f3373d40772239850276da57be226_l3.png)
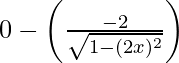
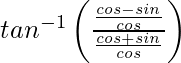
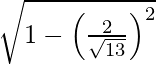
![Rendered by QuickLaTeX.com sin^{-1}\left[\frac{\frac{2sinθ}{cosθ}}{1+\frac{sin^2θ}{cos^2θ}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2d24c4bb96cc1748918916bfac394f18_l3.png)
![Rendered by QuickLaTeX.com sin^{-1}\left[\frac{\frac{2sinθ}{cosθ}}{\frac{cos^2θ+sin^2θ}{cos^2θ}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-18742e0c0322a1587ac817cd437ed921_l3.png)
![Rendered by QuickLaTeX.com sin^{-1}\left[\frac{\frac{2sinθ}{cosθ}}{\frac{1}{cos^2θ}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a47897252e094680ce2b8a1701a32302_l3.png)