Dados dos números enteros L y R , la tarea es calcular el valor de la expresión:
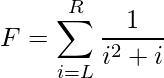
Ejemplos:
Entrada: L = 6, R = 12
Salida: 0,09
Entrada: L = 5, R = 6
Salida: 0,06
Enfoque: Se puede observar que ![]() .
.
Entonces, por lo ![]()
tanto, la respuesta será (1 / L) – (1 / (R + 1)) .
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
// Function to return the value
// of the given expression
double get(double L, double R)
{
// Value of the first term
double x = 1.0 / L;
// Value of the last term
double y = 1.0 / (R + 1.0);
return (x - y);
}
// Driver code
int main()
{
int L = 6, R = 12;
// Get the result
double ans = get(L, R);
cout << fixed << setprecision(2) << ans;
return 0;
}
Java
// Java implementation of the approach
import java.util.*;
class GFG
{
// Function to return the value
// of the given expression
static double get(double L, double R)
{
// Value of the first term
double x = 1.0 / L;
// Value of the last term
double y = 1.0 / (R + 1.0);
return (x - y);
}
// Driver code
public static void main(String []args)
{
int L = 6, R = 12;
// Get the result
double ans = get(L, R);
System.out.printf( "%.2f", ans);
}
}
// This code is contributed by Surendra_Gangwar
Python3
# Python3 implementation of the approach # Function to return the value # of the given expression def get(L, R) : # Value of the first term x = 1.0 / L; # Value of the last term y = 1.0 / (R + 1.0); return (x - y); # Driver code if __name__ == "__main__" : L = 6; R = 12; # Get the result ans = get(L, R); print(round(ans, 2)); # This code is contributed by AnkitRai01
C#
// C# implementation of the approach
using System;
public class GFG
{
// Function to return the value
// of the given expression
static double get(double L, double R)
{
// Value of the first term
double x = 1.0 / L;
// Value of the last term
double y = 1.0 / (R + 1.0);
return (x - y);
}
// Driver code
public static void Main(String []args)
{
int L = 6, R = 12;
// Get the result
double ans = get(L, R);
Console.Write( "{0:F2}", ans);
}
}
// This code contributed by PrinciRaj1992
Javascript
<script>
// JavaScript implementation of the approach
// Function to return the value
// of the given expression
function get(L, R)
{
// Value of the first term
let x = 1.0 / L;
// Value of the last term
let y = 1.0 / (R + 1.0);
return (x - y);
}
// Driver code
let L = 6, R = 12;
// Get the result
let ans = get(L, R);
document.write(Math.round(ans * 100) / 100);
// This code is contributed by Surbhi Tyagi.
</script>
Producción:
0.09
Complejidad de tiempo: O(1)
Espacio Auxiliar: O(1)