Diámetro de un árbol indexado binario con N Nodes

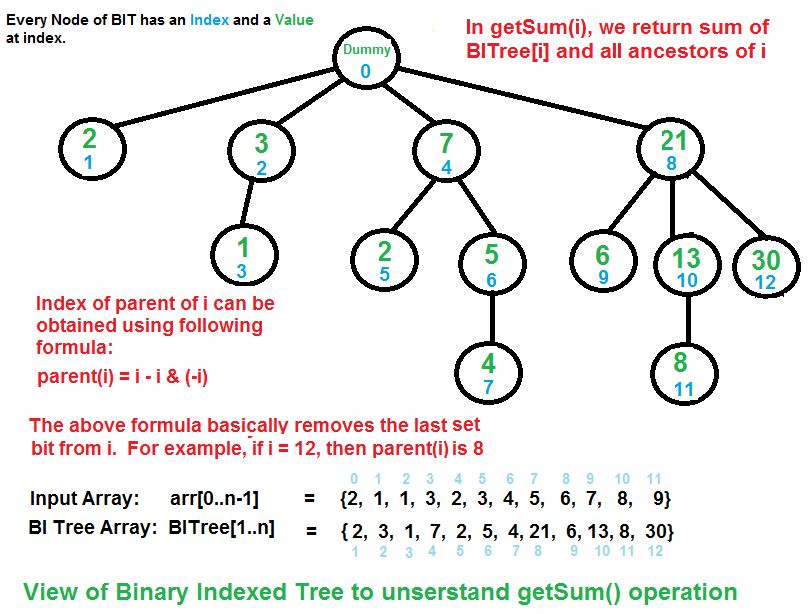
Dado un árbol indexado binario con N Nodes excepto el Node raíz 0 (numerados del 1 al N), encuentre su diámetro. 
Árbol indexado binario es un árbol donde el padre de un número de Node X = X – (X & (X – 1)), es decir, el último bit no está configurado en X. El diámetro de un árbol es el camino simple más largo entre dos hojas cualesquiera. 
Ejemplos: 
 

Entrada: N = 12 
Salida: 6 
Explicación: Ruta del Node 7 al Node 11.
 

Entrada: n = 15  
Salida: 7 
 

Acercarse: 
 

• En un BIT, la raíz es siempre el Node 0. En el primer nivel, todos los Nodes son de potencia 2. (1, 2, 4, 8, ….)
• Considere cualquier Node en el primer nivel (1, 2, 4, 8, ), su subárbol incluirá todos los Nodes que tengan el mismo número de bits que la raíz. 
  1. El subárbol con la raíz 1 no tendrá ningún hijo.
  2. El subárbol con raíz 2 tendrá 3 como hijo.
  3. El subárbol con raíz 4 tendrá 5, 6, 7 como hijo.
  4. El subárbol con raíz 8 tendrá 9, 10, 11, 12, 13, 14, 15 como hijo. (El doble del tamaño del subárbol anterior)
  5. Entonces, el subárbol con raíz K tendrá K Nodes, incluida la raíz. Y la altura de cada subárbol sería igual: 
     • para subárbol con raíz 1
     • para subárbol con raíz 2
     • para subárbol con raíz 4
• Ahora, necesitamos encontrar el subárbol en el que se encuentra N. Digamos que la altura del subárbol justo antes del subárbol en el que se encuentra N es H y el tamaño es L. Por lo tanto, son posibles los siguientes casos: 
  • Caso 1: Cuando N >= L*2 – 1, en tal escenario N está en el último nivel de su subárbol. Por lo tanto, el diámetro será 2*H + 1. (Camino desde la hoja de nivel más bajo del subárbol anterior hasta el N).
     
  • Caso 2: cuando N >= L + L/2 – 1, en tal escenario N está en el nivel H en su subárbol. Por lo tanto, el diámetro será 2*H.
     
  • Caso 3: De lo contrario, es óptimo considerar la longitud máxima de la ruta entre los Nodes hoja de dos subárboles justo antes del subárbol en el que se encuentra N, es decir, el diámetro es 2*H – 1.

A continuación se muestra la implementación del enfoque anterior: 
 

#include <bits/stdc++.h>
using namespace std;
 
// Function to find diameter
// of BIT with N + 1 nodes
int diameter(int n)
{
    // L is size of subtree just before subtree
    // in which N lies
    int L, H, templen;
    L = 1;
 
    // H is the height of subtree just before
    // subtree in which N lies
    H = 0;
 
    // Base Cases
    if (n == 1) {
        return 1;
    }
    if (n == 2) {
        return 2;
    }
    if (n == 3) {
        return 3;
    }
 
    // Size of subtree are power of 2
    while (L * 2 <= n) {
        L *= 2;
        H++;
    }
 
    // 3 Cases as explained in Approach
    if (n >= L * 2 - 1)
        return 2 * H + 1;
    else if (n >= L + (L / 2) - 1)
        return 2 * H;
    return 2 * H - 1;
}
 
// Driver Code
int main()
{
    int n = 15;
    cout << diameter(n) << endl;
}

// Java implementation of the approach
class GFG
{
 
// Function to find diameter
// of BIT with N + 1 nodes
static int diameter(int n)
{
    // L is size of subtree just before subtree
    // in which N lies
    int L, H, templen;
    L = 1;
  
    // H is the height of subtree just before
    // subtree in which N lies
    H = 0;
  
    // Base Cases
    if (n == 1) {
        return 1;
    }
    if (n == 2) {
        return 2;
    }
    if (n == 3) {
        return 3;
    }
  
    // Size of subtree are power of 2
    while (L * 2 <= n) {
        L *= 2;
        H++;
    }
  
    // 3 Cases as explained in Approach
    if (n >= L * 2 - 1)
        return 2 * H + 1;
    else if (n >= L + (L / 2) - 1)
        return 2 * H;
    return 2 * H - 1;
}
  
// Driver Code
public static void main(String []args)
{
    int n = 15;
 
    System.out.println(diameter(n));
}
}
 
// This code contributed by PrinciRaj1992

# Python3 implementation of the approach
 
# Function to find diameter
# of BIT with N + 1 nodes
def diameter(n):
     
    # L is size of subtree just before
    # subtree in which N lies
    L, H, templen = 0, 0, 0;
    L = 1;
 
    # H is the height of subtree just before
    # subtree in which N lies
    H = 0;
 
    # Base Cases
    if (n == 1):
        return 1;
     
    if (n == 2):
        return 2;
     
    if (n == 3):
        return 3;
 
    # Size of subtree are power of 2
    while (L * 2 <= n):
        L *= 2;
        H += 1;
     
    # 3 Cases as explained in Approach
    if (n >= L * 2 - 1):
        return 2 * H + 1;
    elif (n >= L + (L / 2) - 1):
        return 2 * H;
    return 2 * H - 1;
 
# Driver Code
n = 15;
print(diameter(n));
 
# This code is contributed by Rajput-Ji

// C# implementation of the approach
using System;
 
class GFG
{
 
// Function to find diameter
// of BIT with N + 1 nodes
static int diameter(int n)
{
    // L is size of subtree just before subtree
    // in which N lies
    int L, H;
    L = 1;
 
    // H is the height of subtree just before
    // subtree in which N lies
    H = 0;
 
    // Base Cases
    if (n == 1)
    {
        return 1;
    }
    if (n == 2)
    {
        return 2;
    }
    if (n == 3)
    {
        return 3;
    }
 
    // Size of subtree are power of 2
    while (L * 2 <= n)
    {
        L *= 2;
        H++;
    }
 
    // 3 Cases as explained in Approach
    if (n >= L * 2 - 1)
        return 2 * H + 1;
    else if (n >= L + (L / 2) - 1)
        return 2 * H;
    return 2 * H - 1;
}
 
// Driver Code
public static void Main(String []args)
{
    int n = 15;
 
    Console.WriteLine(diameter(n));
}
}
 
// This code is contributed by 29AjayKumar

<script>
 
// Function to find diameter
// of BIT with N + 1 nodes
function diameter(n)
{
    // L is size of subtree just before subtree
    // in which N lies
    var L, H, templen;
    L = 1;
 
    // H is the height of subtree just before
    // subtree in which N lies
    H = 0;
 
    // Base Cases
    if (n == 1) {
        return 1;
    }
    if (n == 2) {
        return 2;
    }
    if (n == 3) {
        return 3;
    }
 
    // Size of subtree are power of 2
    while (L * 2 <= n) {
        L *= 2;
        H++;
    }
 
    // 3 Cases as explained in Approach
    if (n >= L * 2 - 1)
        return 2 * H + 1;
    else if (n >= L + (L / 2) - 1)
        return 2 * H;
    return 2 * H - 1;
}
 
// Driver Code
var n = 15;
document.write( diameter(n));
 
</script>

7

Complejidad de tiempo: O (log n)

Espacio Auxiliar: O(1)