El concepto de límites ha existido durante miles de años, los primeros matemáticos de civilizaciones antiguas usaban límites para aproximar el área de un círculo. Pero el concepto formal no existió hasta el siglo XIX. Este concepto es esencial para el cálculo y sirve como componente básico para analizar derivadas, continuidad y diferenciabilidad. Intuitivamente, los límites nos dan una idea acerca de los valores que la función aproxima a un valor particular de x. Usando esta idea, los límites también se pueden estimar hasta cierto punto simplemente mirando el gráfico. Veamos estas ideas en detalle.
Límite
El límite de una función en un número x = a se puede considerar como el valor de la función que comienza a tomar mientras se acerca a x = a. El punto x = a se puede abordar desde cualquiera de los lados, el lado izquierdo o el lado derecho. Por ejemplo, consideremos una función f(x), entonces el límite de la función en x = a se denota como,
![]()
El límite izquierdo se denota como,
![]()
De manera similar, el límite de la mano derecha se denota como,
![]()
- Si f(x) se acerca cada vez más a un valor específico L a medida que x se acerca a un valor elegido c desde la derecha, entonces se dice que el límite de f(x) cuando x se acerca a c desde la derecha es L.
- Si f(x) se acerca cada vez más a un valor específico L a medida que x se acerca a un valor elegido c desde la izquierda, entonces se dice que el límite de f(x) cuando x se acerca a c desde la izquierda es L.
- Si el límite de f(x) cuando x tiende a c es el mismo por la derecha y por la izquierda, entonces se dice que el límite de f(x) cuando x tiende a c es L.
Si f(x) nunca tiende a un valor finito específico cuando x tiende a c, entonces decimos que el límite no existe. Si f(x) tiene límites derecho e izquierdo diferentes, entonces el límite bilateral (
) no existe.
Los límites de cualquier función se pueden calcular de dos maneras:
- Método algebraico
- Método gráfico
Los métodos algebraicos implican manipular la función de manera que su límite se pueda calcular fácilmente. El método gráfico simplemente implica hacer un gráfico de la función y luego se puede estimar el límite simplemente mirando el gráfico.
Estimación de límites a partir de gráficos
Considere la función f(x),
f(x) = 3x + 4
Esta es una ecuación de una línea. Veamos cuál es el valor del límite de esta función en x = 1. La siguiente figura muestra el gráfico de esta función,

Observe que a medida que nos acercamos tanto del lado izquierdo como del lado derecho de x = 1, la función se mueve hacia un solo valor. Este valor se llama límite de la función.
Límites Ilimitados
A veces hay ciertos tipos de funciones que se mueven hacia el infinito. En tales casos, el valor del límite sube a infinito. Por ejemplo, para la función f(x) dada a continuación,
f(x) = ![]()
El límite para esta función en x = 0,
![]()

Observe en la figura que el límite en x = 0 no está acotado y sube hasta el infinito. Estos límites se denominan límites ilimitados.
Límites unilaterales
A veces las funciones no son continuas, lo que significa que nos dicen dos límites diferentes mientras se acercan desde dos lados diferentes. Por ejemplo, la función entera mayor es inherentemente discontinua y en estas discontinuidades observamos dos valores diferentes.
f(x) =[x]

En x = 1, hay dos valores cuando se aproxima desde dos lados diferentes. En tales casos, generalmente se nos pide que digamos el valor de un lado. Estos se llaman límites unilaterales.
Límites y comportamiento gráfico
Los límites pueden decir mucho sobre el comportamiento de una función en algún punto en particular. Entonces, ¿cómo se debe usar? En los casos en que se sabe que la función es discontinua, se vuelve difícil analizar la gráfica de la función utilizando únicamente derivadas. En tales casos, los límites se pueden usar para encontrar los valores de la función en los puntos de discontinuidades. Por ejemplo, digamos que tenemos una función f(x),
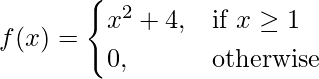
Es obvio a partir de la definición de la función que esta función es discontinua, por lo que las derivadas no son útiles en esos lugares. Ya se conocen las formas gráficas de las piezas individuales, calculemos el valor de la función en la discontinuidad x = 1.
Límite izquierdo en x = 1,
![]()
Límite derecho en x = 1,
![]()
⇒![]()
⇒ 5
Entonces, los valores de ambos límites son diferentes. Ahora podemos trazar la función en un gráfico.

Problemas de muestra
Pregunta 1: Encuentra el ![]()
Responder:
La gráfica de x 2 es una parábola ascendente que está centrada en el origen. La siguiente figura muestra la gráfica de la función dada.
Observe que la función comienza a moverse para tomar un valor de 1 a medida que uno se mueve hacia el valor de x = 1.
De este modo,
Pregunta 2: Encuentra el ![]()
Responder:
La gráfica de log(x) es una función de saturación. La siguiente figura muestra la gráfica de la función dada.
Observe que la función comienza a tomar un valor de -∞ a medida que uno se mueve hacia el valor de x = 0. Este es un ejemplo de límite ilimitado mencionado anteriormente.
De este modo,
Pregunta 3: Encuentra el límite de la función en x = 1.

Solución:
En el gráfico, el punto blanco en x = 1 indica que la función no está definida en x = 1. Eso significa que no debería haber ningún valor de la función en x = 1.
El límite nos permite calcular los valores a los que se aproximaría la función si se hubiera definido en x =1.
Entonces, en este caso del gráfico se puede ver que la función se acerca al valor de 5.
Pregunta 4: Encuentra el valor del límite de la función f(x) = ![]() en x = 0.
en x = 0.
Solución:
La figura muestra el gráfico de la función dada.
La figura deja claro que hay dos límites según desde qué lado nos acerquemos a la función.
Límite del lado izquierdo:
Mientras que acercarse a cero desde el lado negativo del origen lleva la función a infinito negativo.
Límite del lado derecho:
Mientras que acercarse a cero desde el lado positivo del origen lleva la función a infinito positivo.
Pregunta 5: Encuentra el ![]()
Responder:
La gráfica de x 2 es una parábola ascendente que está centrada en el origen. La siguiente figura muestra la gráfica de la función dada.
Observe que la función comienza a moverse para tomar un valor de 1 a medida que uno se mueve hacia el valor de x = 1.
De este modo,
Pregunta 5: Averigüe el límite en x = 0 para la función dada,

Responder:
En la figura, la función dada no es continua en el origen. Eso significa que habrá dos valores diferentes del límite: uno del lado izquierdo y otro del lado derecho.
Límite izquierdo para la función
Derecha: límite de la mano para la función,
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA


