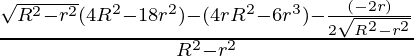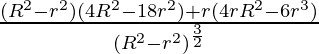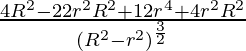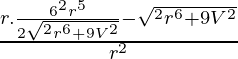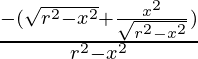Pregunta 16. Una ventana grande tiene la forma de un rectángulo coronado por un triángulo equilátero. Si el perímetro de la ventana es de 12 metros, encuentre las dimensiones del rectángulo que producirá el área más grande de la ventana.
Solución:

Según la pregunta
Supongamos que l es la longitud del rectángulo y b el ancho del rectángulo
El perímetro de la ventana = 12 m
⇒ (l + 2b) + (l + l) = 12
⇒ 3l + 2b = 12 ……(i)
Ahora encontramos el área de la ventana (A) = Área del rectángulo + Área del equilátero △
A = l (12 – 3l / 2) + √3/4 l 2
Al diferenciar wrt l, obtenemos
dA/dl = 6 – 3l + (√3/2)l = 6 – √3(√3 – 1/2)l
Para máximos y mínimos,
Poner dA/dl = 0
⇒ 6 – √3(√3 – 1/2)l = 0
⇒ l = 6/{√3(√3 – 1/2) } = 12- (6 – √3)
Ahora, d 2 A/dl 2 = -√3(√3 – 1/2) = -3 + √3/2
Entonces, l = 12/(6 – √3) es el punto de máximos locales
Entonces, cuando l = 12/(6 – √3), el área de la ventana es máxima
De la ecuación (i), obtenemos
b = (12 – 3l)/2 = [12 – 3{12/(6 – √3)}]/2 = (24 – 6√3)/(6 – √3)
Pregunta 17. Demuestra que la altura del cilindro de máximo volumen que se puede inscribir en una esfera de radio R es 2R/√3. Además, encuentre el volumen máximo.
Solución:
Según la pregunta
R sea el radio de la esfera
Entonces, supongamos que r y h son el radio y la altura del cilindro
Entonces, según la imagen.
h = 2 √(R 2 – r 2 )
Ahora encontramos que el volumen del cilindro es
V = πr 2 h = 2πr 2 √(R 2 – r 2 )
Al diferenciar wrt r, obtenemos
dV/dr = 4πr √(R 2 – r 2 ) +
= 4πr √(R 2 – r 2 ) –
=
=
Para máximos y mínimos,
Poner dV/dr = 0
4πrR 2 – 6πr 3 = 0
r2 = 2R2 / 3
Ahora, de nuevo diferenciando wrt r, obtenemos
d 2 V/ d 2 =
=
=
Entonces, en r 2 = 2R 2 /3, d 2 V/dr 2 < 0
Por tanto, el volumen es máximo cuando r 2 = 2R 2 /3
entonces, la altura del cilindro = 2√(R 2 – 2R 2 /3) = 2√(R 2 /3) = 2R/√3
Por lo tanto probado
Pregunta 18. Un rectángulo está inscrito en un semicírculo de radio r con uno de sus lados en el diámetro del semicírculo. Encuentra las dimensiones del rectángulo para que su área sea máxima. Encuentra también el área.
Solución:
Supongamos que EFGH es un rectángulo inscrito en un semicírculo. Entonces, r es el radio del semicírculo.
Y l y b son la longitud y el ancho del rectángulo.
Ahora en △OHE,
HE 2 = OE 2 – OH 2
ÉL = b =
…..(i)
Ahora encontramos el área del rectángulo EFGH
A = lb = l ×
A = 1/2 l √(4r 2 – l 2 )
Al diferenciar wrt l, obtenemos
dA/dl = 1/2 \sqrt{4r^2-l^2}-\frac{l^2}{\sqrt{4r^2-l^2}}
= 1/2 \frac{4r^2-l^2-l^2}{\sqrt{4r^2-l^2}}
=
Para máximos y mínimos,
Poner dA/dl = 0
⇒
⇒ l = ±√2r
Como sabemos que l no puede ser negativo entonces l ≠ -√2r
Entonces, cuando l = √2r, d 2 A/dl 2 < 0
Por lo tanto, el área del rectángulo es máxima cuando l = √2r
Ahora pon el valor de l = √2r en la ecuación (i), obtenemos
Ahora encontramos el área del rectángulo = lb
= √2r × r/√2
= r 2
Pregunta 19. Demuestre que una tienda cónica de capacidad dada requerirá la menor cantidad de lona cuando la altura es √2 veces el radio de la base.
Solución:
Supongamos que el radio y la altura del cono son r y h.
Entonces, el volumen del cono es
V = 1/3 πr 2 h
h = 3V/r 2 ……(i)
Y el área de la superficie del cono es
A = πrl
Aquí, l es la altura inclinada = √(r 2 + h 2 )
= πr√(r 2 + h 2 )
=
Al diferenciar wrt r, obtenemos
dA/dr =
=
Para máximos y mínimos,
Poner dA/dr = 0
2π 2 r 6 = 9V 2
r 6 = 9V 2 /2π 2
Cuando, r 6 = 9V 2 /2π 2 , d 2 S/dr 2 > 0
Por lo tanto, el área superficial del cono es mínima cuando r 6 = 6V 2 /2π 2
Ahora ponga r 6 = 9V 2 /2π 2 en la ecuación (i), obtenemos
h = 3V/πr 2 = 3/πr 2 ( 2π 2 r 6/9 ) 1/2 = (3/πr 2 ) (√2πr 3/3 ) = √2r
Por lo tanto probado
Pregunta 20. Demostrar que el cono de mayor volumen que se puede inscribir en una esfera dada tiene una altura igual a 2/3 del diámetro de la esfera.
Solución:
Supongamos que R es el radio de la esfera
Entonces, de la figura, obtenemos OD = x y AO = OB = R
BD = √(R 2 – x 2 ) y AD = (R + x)
Ahora,
El volumen del cono es
V = 1/3 πr 2 h
= 1/3 πBD 2 × AD
= 1/3 π (R 2 – x 2 ) × (R + x)
Al derivar wrt x, obtenemos
dV/dx = π/3 [-2x (R + x) + R 2 – x 2 ]
= π/3 [R 2 – 2xR – 3x 2 ]
Para máximo y mínimo
Poner dv/dx = 0
⇒ π/3 [R 2 – 2xR – 3x 2 ] = 0
⇒ π/3 [(R – 3x) (R + x)] = 0
⇒ R – 3x = 0 o x = -R
Aquí, x = -R no es posible porque -r hará que la altitud sea 0
⇒x = R/3
Ahora,
d 2 V/dx 2 = π/3[-2R – 6x]
Entonces, cuando x = R/3, d 2 v/dx 2 = π/3[-2R – 2R] = -4πR/3 < 0
Entonces, x = R/3 es el punto de máximos locales.
Por lo tanto, el volumen es máximo cuando x = R/3
Entonces, la altitud AD = (R + x) = (R + R/3) = 4R/3 = 2/3d
Aquí, d es el diámetro de la esfera.
Pregunta 21. Demostrar que el ángulo semivertical del cono circular recto de volumen dado y superficie menos curvada es cot -1 (√2).
Solución:

Supongamos que h, r y θ son la altura, el radio y el ángulo semivertical del triángulo rectángulo.
Entonces, el volumen del cono (V) = 1/3 πr 2 h
⇒ h = 3V/ πr2
Altura inclinada del cono (l) = √(r 2 + h 2 )
yo =
Y el área de la superficie curva del cono es
A = πrl
A = πr
un =
Al diferenciar wrt r, obtenemos
dA/dr =
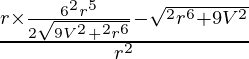
=
Para máximo y mínimo
Poner dA/dr = 0
= 0
⇒ 2π 2 r 6 – 9V 2 = 0
⇒ V 2 = 2π 2 r 6 /9
⇒ V= √2π 2 r 6 /9
⇒ V= πr 3 √2/3
0r
r = (3V/π√2) 1/3
h/r = √2
cotθ = √2
Ángulo semivertical, θ = cot -1 √2
Además, cuando r < (3V/π√2) 1/3 , dA/dr < 0
Cuando r > (3V/π√2) 1/3 , dA/dr > 0
Por lo tanto, la superficie curva para r = (3V/π√2) 1/3 es mínima.
Pregunta 22 Un triángulo isósceles de ángulo vertical 2θ está inscrito en una circunferencia de radio a. Demuestre que el área del triángulo es máxima cuando θ = π/6.
Solución:

Consideremos que ABC es un triángulo isósceles tal que AB = AC
y el ángulo vertical∠BAC = 2θ
Radio del círculo = a
Ahora, dibuja AM perpendicular a BC.
De la figura concluimos que en △ABC es un triángulo isósceles
el circuncentro del círculo se encuentra en la perpendicular de A a BC y
O sea el circuncentro del círculo
Entonces, ∠BOC = 2 × 2θ = 4θ
y ∠COM = 2θ [Ya que △OMB y △OMC son triángulos congruentes]
OA = OB = OC =a [Radio del círculo]
En △OMC,
CM = asen2θ y OM = acos2θ
BC = 2CM [Perpendicular desde el centro biseca la cuerda]
BC = 2asen2θ …..(i)
En △ABC,
AM = AO + OM
AM = a + acos2θ …..(ii)
Ahora el área de △ABC es,
A = 1/2 × BC × AM
= 1/2 × 2asen2θ × (a + acos2θ) ……(iii)
Al derivar wrt θ , obtenemos
dA/dθ = a 2 (2cos2θ + 1/2 × 4cos4θ)
dA/dθ = 2a 2 (cos2θ + cos4θ)
Nuevamente, diferenciando con θ , obtenemos
d2A / dθ2 = 2a2 ( -2sen2θ – 4sen4θ)
Para máximo y mínimo
Poner dA/dθ = 0
2a 2 (cos2θ + cos4θ) = 0
cos2θ + cos4θ = 0
cos2θ + 2cos 2 2θ – 1 = 0
(2cos2θ – 1)(2cos2θ + 1) = 0
cos2θ = 1/2 o cos2θ = -1
2θ = π/3 o 2θ = π
θ = π/6 o θ = π/2
Cuando θ = π/2, no formará un triángulo.
Cuando θ = π/6, d 2 A/dθ 2 < 0
Por lo tanto, el área del triángulo es máxima cuando θ = π/6
Pregunta 23. Encuentra las dimensiones del rectángulo de 36 cm de perímetro que barrerá un volumen lo más grande posible cuando se gire alrededor de uno de sus lados.
Solución:
Supongamos que l, b y V son el largo, el ancho y el volumen del rectángulo.
el perimetro del rectangulo es de 36cm
2(l + b) = 36
l + b = 18
l = 18 – b ……(yo)
El volumen del cilindro que gira alrededor del ancho,
V = πl 2 segundo
V = π(18 – segundo ) 2 segundo
V = π(324 + segundo 2 – 36b) segundo
V = π(324b + segundo 3 – 36b 2 )
Al diferenciar wrt b, obtenemos
dV/db = π(324 + 3b 2 – 72b)
Nuevamente diferenciando wrt b, obtenemos
d 2 V/db 2 = π(6b– 72)
Para máximo y mínimo
Poner dV/db = 0
π(324b + b 3 – 36b 2 ) = 0
(b – 6)(b – 18) = 0
b = 6, 18
Cuando b = 6, d 2 V/db 2 = -36π < 0
Cuando b = 18, d 2 V/db 2 = 36π > 0
Entonces, en b = 6 es el máximo
Por lo tanto, el volumen es máximo cuando b = 6
Ahora pon el valor de b en la ecuación (i), obtenemos
l = 18 – 6
l = 12
Por lo tanto, las dimensiones del rectángulo son 12 cm y 6 cm.
Pregunta 24. Demuestra que la altura del cono de máximo volumen que se puede inscribir en una esfera de 12 cm de radio es de 16 cm.
Solución:
Supongamos que r y h son el radio de la base del cono y la altura del cono.
De la figura OD = x, y R = 12, BD = r
En △DBO,
BD = √(R 2 – x 2 )
= √(144 – x2 )
= (144 – x2 )
y AD = AO + OD
= R + x = 12 + x
El volumen del cono es
V = 1/3 πr 2 h
= 1/3 π BD 2 × AD
= 1/3 π(144 – x 2 )(12 + x)
= 1/3 π(1728 + 144x – 12x 2 – x 3 )
Al derivar wrt x, obtenemos
dV/dx = 1/3π (144 – 24x – 3x 2 )
Para máximo y mínimo
Poner dV/dx = 0
⇒ 1/3 π(144 – 24x – 3x 2 ) = 0
⇒ x = -12, 4
Aquí x = -12 no es posible
Entonces, x = 4
Ahora,
d 2 V/dx 2 = π/3(-24 – 6x)
En x = 4, d 2 v/dx 2 = -2π(4 + x) = -2π × 8 = -16π < 0
Entonces, x = 4 es el punto de los máximos locales.
Por lo tanto, la altura del cono de volumen máximo = R + x
= 12 + 4 = 16cm
Pregunta 25. Un cilindro cerrado tiene un volumen de 2156 cm 3 . ¿Cuál será el radio de su base para que su superficie total sea mínima?
Solución:
Dado que el volumen del cilindro cerrado (V) = 2156 cm 3
Supongamos que r y h son el radio y la altura del cilindro.
Entonces, el volumen del cilindro es
V= πr 2 h = 2156 …..(i)
y la superficie total es
A = 2πrh + 2πr 2
A = 2πr (h + r) …..(ii)
Entonces, de la ecuación (i) y (ii)
A = (2156 × 2)/r + 2πr 2
Al diferenciar wrt r, obtenemos
dA/dr = – 4312/4π + 4πr
Para máximo y mínimo
Poner dA/dr = 0
⇒ (-4312 + 4πr 3 )/r 2 = 0
⇒ r3 = 4312/4π
⇒ r = 7
En r = 7, d 2 s/dr 2 = (8624/r3 + 4π) > 0
Entonces, r = 7 es el punto de mínimos locales
Por lo tanto, el área total de la superficie de contacto del cilindro cerrado será mínima cuando r = 7 cm.
Pregunta 26. Demuestre que el volumen máximo del cilindro que se puede inscribir en una esfera de radio 5√3 cm es 500π cm 3 .
Solución:
Sean r y h el radio y la altura del cilindro.
Dado que R sea el radio de la esfera = 5√3
Entonces, de la figura LM = h, OL = x
Entonces, h = 2x
Ahora, en △AOL,
AL = √(AO 2 – OL 2 )
= √(75 – x2 )
Como sabemos que el volumen del cilindro es
V = πr 2 horas
= πAL 2 × ML
= π(75 – x 2 ) × 2x
Al derivar wrt x, obtenemos
dV/dx = π[150 – 6x 2 ]
Para máximo y mínimo
Poner dV/dx = 0
⇒ π[150 – 6x 2 ] = 0
⇒ x = 5 cm
Además, d 2 v/dx 2 = -12πx
En x = 5, d 2 v/dx 2 = -60πx < 0
Entonces, x = 5 es el punto de los máximos locales.
Por lo tanto, el volumen es máximo cuando x = 5
Entonces, el volumen máximo del cilindro es
= π(75 – 25) × 10 = 500π cm 3
Pregunta 27. Muestre que entre todos los números positivos x e y con x 2 + y 2 = r 2 , la suma x + y es mayor cuando x = y = r/√2.
Solución:
Consideremos que los dos números positivos son x e y con
x 2 + y 2 = r 2 ……(i)
Sea S la suma de dos números positivos
S = x + y …..(ii)
= x + √(r 2 – x 2 ) [De la ecuación (ii)]
Al derivar wrt x, obtenemos
dS/dx = 1 – x/√(r 2 – x 2 )
Para máximo y mínimo
Poner dS/dx = 0
⇒ 1 – x/√(r 2 – x 2 ) = 0
⇒ x = √( r2 – x2 )
⇒ 2x 2 = r 2
⇒ x = r/√2, -r/√2
De acuerdo con la pregunta x e y son los números positivos
Entonces, x ≠ -r/√2
Ahora, d 2 S/dx 2 =
En, x = r/√2, d 2 S/dx 2 =
< 0
Entonces, x = r/√2 es el punto de los máximos locales.
Por lo tanto, la suma es máxima cuando x = y = r/√2
Pregunta 28. Determine los puntos de la curva x 2 = 4y que están más cerca del punto (0, 5).
Solución:
La ecuación dada de la parábola es
x2 = 4y …….(i)
Consideremos que P(x, y) es el punto de la parábola dada más cercano al punto A (0, 5)
Sea Q el cuadrado de la distancia de P a A
Q = x 2 + (y – 5) 2 …..(ii)
Q = 4y + (y – 5) 2
Al diferenciar wrt y, obtenemos
⇒ dQ/dy = 4 + 2(y – 5)
Para máximo y mínimo
Ponga dQ/dy = 0
⇒ 4 + 2(y – 5) = 0
⇒ 2 años = 6
⇒ y = 3
De la ecuación (i), obtenemos
× 2 = 12
x = 2√3
⇒ P = (2√3, 3) y p’ = (-2√3, 3)
Ahora,
d 2 Q/ día 2 = 2 > 0
Entonces, P y P’ son el punto de los mínimos locales.
Por lo tanto, los puntos más cercanos son P(2√3, 3) y P”(2√3, 3).
Pregunta 29. Encuentra el punto de la curva y 2 = 4x que está más cerca del punto (2, -8).
Solución:
La ecuación dada de la curva es
y 2 = 4x ….(1)
Supongamos que P(x, y) es un punto en la curva dada y
Sea Q el cuadrado de la distancia entre A(2,-8) y P.
Entonces, Q = (x – 2) 2 + (y + 8) 2 …….(ii)
= (y 2 /4 – 2) 2 + (y + 8) 2
Al diferenciar wrt y, obtenemos
dQ/dy = 2(y 2 /4 – 2) × y/2 + 2(y + 8)
= (y 3 – 8y)/4 + 2y + 16
= y 3 /4 + 16
Para máximo y mínimo
Ponga dQ/dy = 0
⇒ y 3 /4 + 16 = 0
⇒ y = -4
Ahora,
d 2 Q/ día 2 = 3y 2 /4
En y = -4, d 2 S/dy 2 = 12 > 0
Ao, y = -4 es el punto de mínimos locales
Ahora ponga el valor de y en la ecuación (i), obtenemos
x = y 2 /4 = 4
Por lo tanto, el punto es (4, -4) que es el más cercano a (2, -8).
Pregunta 30. Encuentra el punto de la curva x 2 = 8y que está más cerca del punto (2, 4).
Solución:
La ecuación dada de la curva es
x2 = 8y ….(1)
Sea P(x, y) un punto en la curva dada, y
Q sea el cuadrado de la distancia entre P y A(2, 4).
Q = (x – 2) 2 + (y – 4) 2 ……..(ii)
= (x – 2) 2 + (x 2 /8 – 4) 2
Al derivar wrt x, obtenemos
dQ/dx = 2(x – 2) + 2(x 2 /8 – 4) × 2x/8
= 2(x – 2) + (x2 – 32)x/16
Además, d 2 Q/dx 2 = 2 + 1/16[x 2 – 32 + 2x 2 ]
= 2 + 1/16[3x 2 – 32]
Para máximos y mínimos,
dQ/dx = 0
⇒ 2(x – 2) + x(x 2 – 32)/16 = 0
⇒ 32x – 64 + x3 -32x = 0
⇒ x 3 – 64 = 0
⇒ x = 4
En x = 4, d 2 Q/dx 2 = 2 + 1/16[16 × 3 – 32] = 2 + 1 = 3 > 0
Entonces, x = 4 es el punto de mínimos locales
Ahora pon el valor de x en la ecuación (1), obtenemos
y = x 2 /8 = 2
Entonces, el P(4, 2) es el punto más cercano a (2, 4)
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA