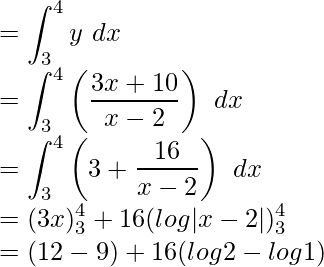Pregunta 11. Dibuja la región {(x, y) : 9x 2 + 4y 2 = 36} y encuentra el área encerrada por ella, usando integración.
Solución:
9×2 + 4y2 = 36
Área del Sector OABCO =
Área de toda la figura = 4 x área de DOABCO
Pregunta 12. Dibuja un bosquejo aproximado de la gráfica de la función  , x
, x
Solución:
Aquí, tenemos que encontrar el área encerrada entre la curva y el eje x.
La ecuación (1) representa una elipse con centro en el origen y pasa por (±1, 0) y (0, ±2) y x ∈ [0, 1] representada por la región entre el eje y y la línea x = 1.
Aquí, está el boceto aproximado.
La región sombreada representa el área requerida.
Lo cortamos en un rectángulo de aproximación de
Ancho = △x
Longitud = y
Área del rectángulo = y△x
Los rectángulos aproximados se deslizan de x = 0 a x = 1,
De este modo,
Área requerida = Región OAPBO
área requerida =
unidades cuadradas
Aquí,
Tenemos que encontrar el área bajo la curva.
x2 + y2 = un ………..(1)
entre x = 0 ………(2)
x = un ………..(3)
La ecuación (1) representa un círculo con Centro (0, 0) y pasa ejes en (0, ±a), (±a, 0).
La ecuación (2) representa el eje y y
La ecuación x = a representa una línea paralela al eje y que pasa por (a, 0)
Aquí, está el boceto aproximado,
La región sombreada representa el área requerida.
Lo cortamos en un rectángulo de aproximación de
Ancho = △x
Longitud = y
Área del rectángulo = y△x
Los rectángulos aproximados se deslizan de x = 0 a x = a,
De este modo,
Área requerida = Región OAPBO
área requerida =
unidades cuadradas
Aquí,
Tenemos que encontrar el área delimitada por el eje x
2y + 5x = 7 ………(1)
x = 2 ……..(2)
x = 8 ………(3)
La ecuación (1) representa la línea que pasa
y la
ecuación.
La ecuación (2), (3) muestra una línea paralela al eje y que pasa por (2, 0), (8, 0) respectivamente.
Aquí, está el bosquejo aproximado;
La región sombreada representa el área requerida.
Lo cortamos en un rectángulo de aproximación de
Ancho = △x
Longitud = y
Área del rectángulo = y△x
Los rectángulos aproximados se deslizan de x = 2 a x = 8,
De este modo,
Área requerida = Región ABCDA
Área requerida = 96 unidades cuadradas
Aquí, tenemos que encontrar el área del círculo,
x2 + y2 = a2
La ecuación (1) representa un círculo con centro (0, 0) y radio a, por lo que cumple con los ejes (±a, 0), (0, ±a).
Aquí, está el bosquejo aproximado;
La región sombreada representa el área requerida.
Lo cortamos en un rectángulo de aproximación de
Ancho = △x
Longitud = y
Área del rectángulo = y△x
Los rectángulos aproximados se deslizan de x = 0 a x = a,
De este modo,
Área requerida = Región ABCDA
= 4 (Región ABOA)
Aquí, tenemos que encontrar el área encerrada por;
x = -2,
x = 3,
y = 0 y
y = 1 + |x + 1|
⇒ y = 1 + x + 1, si x + 1 0
⇒ y = 2 + x ……….(1), si x ≥ -1
y
⇒ y = 1 – (x + 1), si x + 1 < 0
⇒ y = 1 – x – 1, si x < -1
⇒ y = -x ………(2), si x < -1
De este modo,
La ecuación (1) es una línea recta que pasa por (0, 2) y (-1, 1).
La ecuación (2) es una recta que pasa por (-1, 1) y (-2, 2) y está delimitada por las rectas x = 2 y x = 3, que son rectas paralelas al eje y y pasan por (2, 0 ) y (3, 0) respectivamente y = 0 es el eje x
Aquí está el boceto aproximado
La región sombreada representa el área requerida.
De este modo,
Área requerida = Región (ABECDFA)
Área requerida = (Región ABEFA + Región ECDFE) ……..(1)
Región ECDFE
Lo cortamos en un rectángulo de aproximación de
Ancho = △x
Longitud = y1
Área del rectángulo = y1△x
Los rectángulos aproximados se deslizan de x = -2 a x = -1,
Región ABEFA
Lo cortamos en un rectángulo de aproximación de
Ancho = △x
Longitud = y2
Área del rectángulo = y2△x
Los rectángulos aproximados se deslizan de x = -1 a x = 3,
Área requerida =
área requerida =
unidades cuadradas
Aquí, está el bosquejo del gráfico dado:
y = |x – 5|
Por eso,
Área requerida =
De este modo,
La integral dada representa el área delimitada por las curvas que son,
x = 0,
y = 0,
X = 1
y
y = -(x – 5).
Pregunta 18. Dibuja la gráfica de y = |x + 3| y evaluar 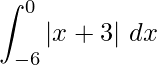 ¿Qué representa esta integral en la gráfica?
¿Qué representa esta integral en la gráfica?
Solución:
Aquí,
La ecuación dada es y = |x + 3|
Los valores correspondientes de x e y se dan en la siguiente tabla.
X -6 -5 -4 -3 -2 -1 0 y 3 2 1 0 1 2 3 De este modo,
Después de trazar estos puntos,
Obtendremos la gráfica de y = |x + 3|
Se muestra como;
Se sabe que (x + 3) ≤ 0 para -6 ≤ x ≤ -3 y (x + 3) ≥ 0 para -3 ≤ x ≤ 0
Por lo tanto,
Pregunta 19. Dibuja la gráfica y = |x + 1|. evaluar 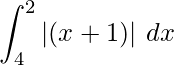 _ ¿Qué representa el valor de esta integral en este gráfico?
_ ¿Qué representa el valor de esta integral en este gráfico?
Solución:
Aquí,
Dado:
y = |x + 1|=
y = x + 1 …………(1)
y
y = -x – 1 ……….(2)
La ecuación (1) representa una línea que se encuentra con los ejes en (0, 1).
La ecuación (2) representa una línea que pasa por (0, -1) y (-1, 0)
Aquí está el boceto aproximado
Área requerida = 9 unidades cuadradas.
Pregunta 20. Encuentra el área de la región delimitada por la curva xy – 3x – 2y – 10 = 0, eje x y las líneas x = 3, x = 4.
Solución:
Aquí,
Tenemos que encontrar el área delimitada por
eje x,
x = 3,
x = 4
y
xy – 3x -2y – 10 = 0
⇒ y(x – 2) = 3x + 10
⇒
Aquí, está el boceto aproximado.
La región sombreada representa el área requerida.
Lo cortamos en un rectángulo de aproximación de
Ancho = △x
Longitud = y
Área del rectángulo = y△x
Los rectángulos aproximados se deslizan de x = 3 a x = 4,
Área requerida = Región ABCDA
Área requerida = (3 + 16 log2) unidades cuadradas.
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA


![Rendered by QuickLaTeX.com \displaystyle \int_0^2\sqrt{\frac{36-9x^2}{4}}\ dx\\ =\frac{3}{2}\int_0^2\sqrt{4-x^2}\ dx\\ =\frac{3}{2}\left[\frac{x\sqrt{4-x^2}}{2}+\frac{2^2}{2}sin^{-1}\left(\frac{x}{2}\right)\right]_0^2\\ =\frac{3}{2}\left[\frac{2\sqrt{4-2^2}}{2}+\frac{2^2}{2}sin^{-1}\left(\frac{2}{2}\right)\right]-\frac{3}{2}\left[\frac{0\sqrt{4-0^2}}{2}+\frac{2^2}{2}sin^{-1}\left(\frac{0}{2}\right)\right]\\ =\frac{3}{2}\times2\times\frac{\pi}{2}-0\\ =\frac{3\pi}{2}\ sq.\ units](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bdf39fc937adba83b48121b6dd84b441_l3.png)
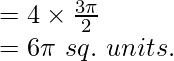
![Rendered by QuickLaTeX.com y=2\sqrt{1-x^2},\ x\ ∈\ [0,\ 1 ]\\ \Rightarrow y^2+4x^2=4,\ x\ ∈\ [0,\ 1]\\ \Rightarrow \frac{x^2}{1}+\frac{y^2}{4},\ x\ ∈\ [0,\ 1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-434207a7f565e59f1b2845c87cb01749_l3.png)

![Rendered by QuickLaTeX.com \displaystyle =\int_0^1y\ dx\\ =\int_0^12\sqrt{1-x^2}\ dx\\ =2\left[\frac{x}{2}\sqrt{1-x^2}+\frac{1}{2}sin^{-1}(x)\right]_0^1\\ =2\left[\left(\frac{1}{2}\sqrt{1-x^2}+\frac{1}{2}sin^{-1}(1)\right)-(0+0)\right]\\ =2\left[0+\frac{1}{2}\times\frac{\pi}{2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2562246359fb868b0ab589d4a1fc082f_l3.png)

![Rendered by QuickLaTeX.com \displaystyle =\int_0^ay\ dx\\ =\int_0^a\sqrt{a^2-x^2}\ dx\\ =\left[\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}sin^{-1}\frac{x}{a}\right]_0^a\\ =\left[\left(\frac{a}{2}\sqrt{a^2-a^2}+\frac{a^2}{2}sin^{-1}(1)\right)-(0)\right]\\ =2\left[0+\frac{a^2}{2}\times\frac{\pi}{2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-93ab57e2d3d4ccfe64559fe18dd43043_l3.png)

![Rendered by QuickLaTeX.com \displaystyle =\int_2^8\left(\frac{5x+7}{2}\right)\\ =\frac{1}{2}\left(\frac{5x^2}{2}+7x\right)_2^8\\ =\frac{1}{2}\left[\left(\frac{5(8)^2}{2}+7(8)\right)-\left(\frac{5(2)^2}{2}+7(2)\right)\right]\\ =\frac{1}{2}[(160+56)-(10+14)]\\ =\frac{192}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cabd17649f4c6bce44e0e558c747c18c_l3.png)

![Rendered by QuickLaTeX.com \displaystyle =4\int_0^ay\ dx\\ =4\int_0^a\sqrt{a^2-x^2}\ dx\\ =4\left[\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}sin^{-1}\frac{x}{a}\right]_0^a\\ =4\left[\left(\frac{a}{2}\sqrt{a^2-a^2}+\frac{a^2}{2}sin^{-1}(1)\right)-(0+0)\right]\\ =4\left[0+\frac{a^2}{2}\times\frac{\pi}{2}\right]\\ =4\left(\frac{a^2\pi}{4}\right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9207e9fb74db70a7f579908fc853c36a_l3.png)

![Rendered by QuickLaTeX.com \displaystyle \int_{-2}^{-1}y_1\ dx+\int_{-1}^3y_2\ dx\\ =-\left[\frac{x^2}{2}\right]^{-1}_{-2}+\left[\frac{x^2}{2}+2x\right]_{-1}^3\\ =-\left[\frac{1}{2}+\frac{4}{2}\right]+\left[\left(\frac{9}{2}+6\right)-\left(\frac{1}{2}-2\right)\right]\\ =\frac{3}{2}+\left(\frac{21}{2}+\frac{3}{2}\right)\\ =\frac{27}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ea3a439528ce57e6200a788dd12f7ddc_l3.png)
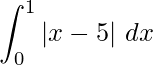

![Rendered by QuickLaTeX.com \displaystyle =\int_0^1y\ dx\\ =\int_0^1|x-5|\ dx\\ =\int_0^1-(x-5)\ dx\\ =\left[\frac{-x^2}{2}+5x\right]_0^1\\ =\left[-\frac{1}{2}+5\right]\\ =\frac{9}{2}\ sq.\ units](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-126fd5932752b43cada6a73749de8ffb_l3.png)

![Rendered by QuickLaTeX.com \displaystyle \int_{-6}^0|(x+3)|\ dx=-\int_{-6}^{-3}(x + 3)\ dx\\ =-\left[\frac{x^2}{2}+3x\right]_{-6}^{-3}+\left[\frac{x^2}{2}+3x\right]_{-3}^0\\ =\left[\left(\frac{(-3)^2}{2}+3(-3)\right)-\left(\frac{(-6)^2}{2}+3(-6)\right)\right]+\left[0-\frac{(-3)^2}{2}+3(-3)\right]\\ =-\left[-\frac{9}{2}\right]-\left[-\frac{9}{2}\right]\\ =9](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f4c2ebae7cc2c8d808cb39f38cd42af4_l3.png)
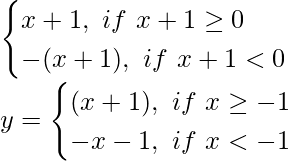

![Rendered by QuickLaTeX.com \displaystyle \int_{4}^2|(x+1)|\ dx=-\int_{-4}^{-1}(x + 1)\ dx\ +\int_{-1}^2(x+1)\ dx\\ =-\left[\frac{x^2}{2}+x\right]_{-4}^{-1}+\left[\frac{x^2}{2}+x\right]_{-1}^2\\ =-\left[\left(\frac{1}{2}-1\right)-\left(\frac{16}{2}-4\right)\right]+\left[\left(\frac{4}{2}+2\right)-\left(\frac{1}{2}-1\right)\right]\\ =-\left[\left(-\frac{1}{2}-4\right)\right]+\left[4+\frac{1}{2}\right]\\ =\frac{9}{2}+\frac{9}{2}\\ =\frac{18}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-25b01443cfbd38702c16b9f38c0a7d42_l3.png)