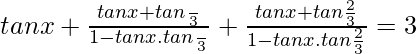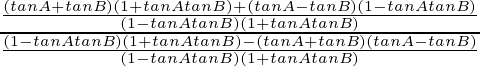Pregunta 17. Demostrar que:
(i) tan 8x – tan 6x – tan 2x = tan 8x tan 6x tan 2x
(ii) tan π/12 + tan π/6 + tan π/12 tan π/6 = 1
(iii) tan 36 ° + tan 9° + tan 36° tan 9° = 1
(iv) tan 13x – tan 9x – tan 4x = tan 13x tan 9x tan 4x
Solución:
(i) Demuestre: tan 8x – tan 6x – tan 2x = tan 8x tan 6x tan 2x
Prueba:
Resolvamos LHS
= tan 8x – tan 6x – tan 2x
= bronceado 8x
= tan(6x + 2x)
Como sabemos que
tan(A + B) = (tanA + tanB) / (1 – tanA tanB)
Asi que,
= tan 8x (tan 6x + tan 2x)/(1 tan 6x tan 2x)
Ahora, multiplicando en cruz obtenemos,
= tan 8x (1 – tan 6x tan 2x) = tan 6x + tan 2x
= bronceado 8x – bronceado 8x bronceado 6x bronceado2x = bronceado 6x + bronceado 2x
Después de reorganizar obtenemos,
= tan 8x – tan 6x – tan 2x = tan 8x tan 6x tan 2x
= lado derecho
LHS = RHS
Por lo tanto probado.
(ii) Demuestre: tan π/12 + tan π/6 + tan π/12 tan π/6 = 1
Prueba:
Como sabemos que
π/12 15° y π/6 = 30°
Entonces, tenemos 15° + 30° = 45°
bronceado (15° +30°) = bronceado 45°
Ya que, tan (A + B)= (tan A+ tan B) / (1 – tanA tanB)
Asi que,
(bronceado 15°+bronceado 30°)/(1-bronceado 15° bronceado 30°) = 1
bronceado 15° bronceado 30° = 1 – bronceado 15° bronceado 30°
Después de reorganizar obtenemos,
tan15° + tan30° + tan 15° tan30° = 1
Por lo tanto probado.
(iii) Demostrar: tan 36° + tan 9° + tan 36° tan 9° = 1
Prueba:
Como sabemos que
36° + 9° = 45°
bronceado (36° + 9°) = bronceado 45°
Dado que, tan (A + B) = (tan A + tan B)/(1 – tanA tanB)
Asi que,
(bronceado 36° + bronceado 9°)/(1 – bronceado 36° bronceado 9°) = 1
bronceado 36° + bronceado 9° = 1 – bronceado 36° bronceado 9°
Después de reorganizar obtenemos,
bronceado 36° + bronceado 9° + bronceado 36° bronceado 9° = 1 = RHS
LHS = RHS
Por lo tanto probado.
(iv) Demuestre: tan 13x-tan 9x-tan 4x = tan 13x tan 9x tan 4x
Prueba:
Vamos a resolver LHS,
= bronceado 13x – bronceado 9x – bronceado 4x
⇒ bronceado 13x = bronceado (9x + 4x)
Sabemos,
tan(A + B) = (tanA + tanB)/(1 – tanA tanB)
Asi que,
tan 13x = (tan 9x + tan 4x)/(1 – tan 9x tan 4x)
Ahora al multiplicar en cruz obtenemos,
tan 13x (1-tan 9x tan 4x) = tan 9x + tan 4x
bronceado 13x – bronceado 13x bronceado 9x bronceado 4x = bronceado 9x + bronceado 4x
Después de reorganizar obtenemos,
tan 13x – tan 9x – tan 4x = tan 13x tan 9x tan 4x = RHS
LHS = RHS
Por lo tanto probado.
Pregunta 18. Probó que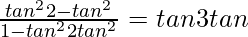
Solución:
Demostrar:
Prueba:
Resolvamos RHS,
= tan3θ tanθ
= tan(2θ + θ) x tan(2θ – θ)
=
=
= LHS
LHS = RHS
Por lo tanto probado
Pregunta 19. Si 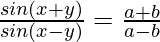 , demuestre que tanx/tany = a/b
, demuestre que tanx/tany = a/b
Solución:
Dado que
⇒
⇒
Ahora usando componendo y Dividendo, obtenemos
⇒
⇒tanx/tany = a/b
Por lo tanto Probado.
Pregunta 20. Si tanA = x tanB, demuestre que 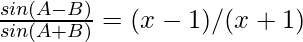
Solución:
Dado que
tanA = x tanB
senA/cosA = x senB/cosB
⇒ senAcosB = x cosA senB
Ahora,
=
=
= (x – 1)(x + 1)
Por lo tanto Probado.
Pregunta 21. Si tan(A + B) = x y tan(A – B) = y, encuentre los valores de tan2A y tan2B.
Solución:
Dado que
tan(A + B) = x y tan(A – B) = y
Como sabemos que tan2A = tan[(A+B) + (AB)]
=
= (x + y) / (1 – xy)
Ya que, tan2B = tan[(A + B) – (A – B)]
Asi que,
=
= (x – y) / (1 + xy)
Pregunta 22. Si cosA + sinB = m y sinA + sinB = n, prueba que 2sin(A + B) = m 2 + n 2 – 2
Solución:
Dado que
cosA + senB = m y senA + cosB = n
Demostrar: 2sen(A + B) = m 2 + n 2 – 2
Prueba:
Resolvamos RHS, m 2 + n 2 – 2
= (cosA + senB) 2 + (senA + cosB) 2 – 2
= cos2A + sen2B + 2cosA senB + sen2A + cos2B + 2 senA cosB – 2
= (sen 2 A + cos 2 A) + (sen 2 B + cos 2 B) + 2 cosA senB + 2 senA cosB – 2
= 1 + 1 + 2 cosA senB + 2 senA cosB – 2
= 2 + 2(senA cosB + cosA senB) – 2
= 2(senA cosB + cosA senB)
= 2 sen(A + B)
LHS = RHS
Por lo tanto Probado.
Pregunta 23. Si tanA + tanB = a y cotA + cotB = b, demuestre que cot(A + B) = 1/a – 1/b.
Solución:
Dado que
tanA + tanB = a y cotA + cotB = b
Demostrar: cot(A + B) = 1/a – 1/b.
Prueba:
Resolvamos cotA + cotB = b
⇒ 1/tanA + 1/tanB = b
⇒ (tanA + tanB)/(tanA tanB) = b
⇒ a/(tanA tanB) = b
⇒ a/b = tanA tanB
Ahora lwts resuelve LHS = cot (A + B) = 1/ tan (A + B)
= 1 / (tanA + tanB)/(1 – tanA tanB)
= (1 – tanA tanB)(tanA + tanB)
= (1 – a/b) / a
= (ba)/ab
= b/ab – a/ab
= 1/a – 1/b
Por lo tanto probado.
Pregunta 24. Si θ está en el primer cuadrante y cosθ = 8/17, entonces prueba que:
cos(π/6 + θ) + cos(π/4 – θ) + cos(2π/3 – θ) = {(√3 – 1)/2 + 1/√2}23/17.
Solución:
Dado,
0 <x <π/2
Ahora, senx =
Resolvamos LHS = cos(π/6 + x) + cos(π/4 – x) + cos(2π/3 – x)
= cos 30° cosx – sen 30° senx + cos 45° cosx + sen 45° senx +
cos 120° cosx + sen 120° senx= cosx (cos 30° + cos 45° + cos 120°) + senx (- sen 30° + sen 45° + sen 120°)
= (8/17)(√3/2 + 1/√2 – 1/2) + (15/17)(-1/2 + 1/√2 + √3/2)
= (8/17)((√3-1)/2 + 1/√2) + (15/17)((√3 – 1)/2 + 1/√2)
= (23/17)((√3-1)/2 + 1/√2)
= lado derecho
LHS = RHS
Por lo tanto probado
Pregunta 25. tanx + tan(x + π/3) + tan(x + 2π/3) = 3, luego prueba que (3tanx – tan 3 x)/(1 – 3tan 2 x) = 1
Solución:
Dado,
tanx + tan(x + π/3) + tan(x + 2π/3) = 3
Demostrar: (3tanx – tan 3 x)/(1 – 3tan 2 x) = 1
Prueba:
⇒
⇒
⇒
⇒
⇒
Por lo tanto probado.
Pregunta 26. Si sen(α + β) = 1 y sen(α – β) = 1/2, donde 0 ≤ α, β ≤ π/2, entonces encuentre los valores de tan(α + 2β) y tan(2α + β)
Solución:
Dado,
sin(α + β) = 1 y sin(α – β) = 1/2
Encuentre los valores de tan(α + 2β) y tan(2α + β)
Asi que,
⇒ α + β = 90° …..(i)
y α – β = 30° …..(ii)
Ahora sumando la ecuación (i) y la ecuación (ii) obtenemos,
⇒ 2α = 120°
⇒ α = 60°
Y al restar la ecuación (ii) de la ecuación (i), obtenemos,
⇒ 2β = 60°
⇒ β = 30°
Asi que,
tan(α + 2β) = tan(60° + 2 × 30°) = tan120° = -√3
tan(2α + β) = tan(2 × 60° + 30°) = tan150° = -1/√3
Pregunta 27. Si α, β son dos valores diferentes de x que se encuentran entre 0 y 2π, que satisfacen la ecuación 6cosx + 8sinx = 9, encuentra el valor de sin(α + β).
Solución:
Dado,
6 cosx + 8 senx = 9
⇒ 6 cosx = 9 – 8 senx
⇒ 36 cos 2 x = (9 – 8 senx) 2
⇒ 36(1 – sen 2 x) = 81 + 64 sen 2 x – 144 senx
⇒ 100 sen 2 x – 144 sen x + 45 = 0
Ahora, consideremos que α y β son las raíces de la ecuación dada,
Entonces, cosα y cosβ son las raíces de la ecuación anterior.
⇒ sinα sinβ = 45/100
Otra vez,
6 cos x + 8 sen x = 9
⇒ 8senx = 9 – 6 cosx
⇒ 64 sen 2 x = (9 – 6 cosx) 2
⇒ 64(1 – cos 2 x) = 81 + 36 cos 2 x – 108 cos x
⇒ 100 cos 2 x – 108 cos x + 17 = 0
Ahora, consideremos que α y β son las raíces de la ecuación dada,
Entonces, sinα y sinβ son las raíces de la ecuación anterior.
entonces, cosα cosβ = 17/100
Por tanto, cos(α + β) = cosα cosβ – sinα sinβ
= 17/100 – 45/100
= -28/100
= -7/25
sen(α + β) = √(1 – cos 2 (α + β))
= √(1 – (-7/25) 2 )
= √(576/625
= 24/25
Pregunta 28 (i), Si senα + senβ = a y cosα + cosβ = b, demuestre que sen(α + β) = 2ab/(a 2 + b 2 )
Solución:
Dado que, sinα + sinβ = a y cosα + cosβ = b
Mostrar: sen(α + β) = 2ab/(a 2 + b 2 )
Entonces, ahora resuelve b 2 + a 2 = (cosα + coβ) 2 + ( sinα + sinβ) 2
= (cos 2 α + sen 2 α) + (sen 2 β + cos 2 β) + 2(cosα cosβ + senα senβ)
= 1 + 1 + 2 cos(α – β)
= 2 + 2 cos(α – β) ……..(i)
y,
b 2 – a 2 = (cosα + coβ) 2 – ( sinα + sinβ) 2
= cos 2 α + cos 2 β – sen 2 α – sen 2 β + 2(cosα cosβ – senα senβ)
= (cos 2 α – sen 2 α) + (cos 2 β – sen 2 β) + 2 cos (α + β)
= 2cos(α + β)cos(α – β) + 2cos(α + β)
= cos(α + β){2cos(α – β) + 2}
= cos(α + β)(b 2 + a 2 ) …….(ii)
⇒ (b 2 – a 2 )/(b 2 + a 2 ) = cos(α + β)
⇒ sen(α + β) = √(1 – cos 2 (α + β))
=
= 2ab/(a 2 + b 2 )
Pregunta 28 (ii). Si senα + senβ = a y cosα + cosβ= b, demuestre que cos(α + β) = (b 2 – a 2 )/(b 2 + a 2 )
Solución:
Dado que, sinα + sinβ = a y cosα + cosβ= b
Mostrar: cos(α + β) = (b 2 – a 2 )/(b 2 + a 2 )
Entonces, ahora resuelve b 2 + a 2 = (cosα + coβ) 2 + ( sinα + sinβ) 2
= (cos 2 α + sen 2 α) + (sen 2 β + cos 2 β) + 2(cosα cosβ + senα senβ)
= 1 + 1 + 2 cos(α – β)
= 2 + 2 cos(α – β) ……(i)
y,
b 2 – a 2 = (cosα + coβ) 2 – ( sinα + sinβ) 2
= cos 2 α + cos 2 β – sen 2 α – sen 2 β + 2(cosα cosβ – senα senβ)
= (cos 2 α – sen 2 α) + (cos 2 β – sen 2 β) – 2 cos (α + β)
= 2cos(α + β) cos(α – β) + 2cos(α – β)
= cos(α + β) {2cos(α – β) + 2} ……..(ii)
Ahora de (i) y (ii), tenemos
⇒ b 2 – a 2 = cos(α + β)(a 2 + b 2 )
⇒ (b 2 – a 2 )/(b 2 + a 2 ) = cos(α + β)
Pregunta 29 (i). probado que 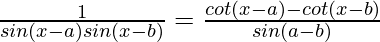
Solución:
Resolvamos RHS
=
=
=
=
=
=
= LHS
LHS = RHS
Por lo tanto probado.
Pregunta 29 (ii). probado que 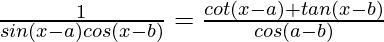
Solución:
Resolvamos RHS
=
=
=
=
=
=
= lado derecho
LHS = RHS
Por lo tanto Probado.
Pregunta 29 (iii). probado que 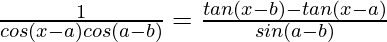
Solución:
Resolvamos RHS
=
=
=
=
=
=
= LHS
LHS = RHS
Por lo tanto probado
Pregunta 30. Si sinα sinβ – cosα cosβ + 1 = 0, se demostró que 1 + cotα tanβ = 0
Solución:
Dado,
sinα sinβ – cosα cosβ + 1 = 0
⇒ -(cosα cosβ – sinα sinβ) + 1 = 0
⇒ -cos(α + β) + 1 = 0
⇒ cos(α + β) = 1
Por tanto, sen(α + β) = 0 ……(i)
Resolvamos LHS
= 1 + cotα tanβ = 1 + (cosα sinβ)/(sinα cosβ)
= (sinα cosβ + cosα sinβ)/ (sinα cosβ)
= sin(α + β)/ (sinα cosβ)
Ahora de la ecuación (i), obtenemos
= 0
LHS = RHS
Por lo tanto Probado.
Pregunta 31. tanα = x + 1 y tanβ = x – 1, demuestra que 2cot(α – β) = x 2
Solución:
Tenemos,
tanα = x + 1 y tanβ = x – 1
Como sabemos que tan(α – β) = (tanα – tanβ) / (1 + tanα tanβ)
= [(x + 1) – (x – 1)] / [1 + (x + 1)(x – 1)]
= (x + 1 – x + 1) / (1 + x 2 – 1)
= 2/ (1 + x 2 – 1)
= 2/ x2
cuna(α – β) = x 2 /2
2cot(α – β) = x 2
LHS = RHS
Por lo tanto Probado.
Pregunta 32. Si el ángulo θ se divide en dos partes tales que las tangentes de una parte son λ partes por la tangente de la otra, y ϕ es su diferencia, entonces demuestre que senθ = (λ + 1)/(λ – 1) senϕ .
Solución:
Consideremos α y β como las dos partes del ángulo θ.
Entonces, θ = α + β y ϕ = α – β
Según la pregunta, obtenemos
tanα = λ tanβ
⇒ tanα / tanβ = λ/1
Ahora, aplicando componendo y dividendo, obtenemos
⇒ (tanα + tanβ) / (tanα – tanβ) = (λ+1) / (λ-1)
⇒
⇒
⇒
⇒
⇒
Por lo tanto probado.
Pregunta 33. Si tanθ = (sinα – cosα)/(sinα + cosα), entonces demuestre que sinα + cosα = √2cosθ
Solución:
Dado que tanθ = (sinα – cosα)/(sinα + cosα)
Ahora, al dividir el numerador y el denominador por cosα, obtenemos
⇒ tanθ = (tanα – 1)(tanα + 1)
⇒ tanθ = (tanα – tan(π/4))(1+tan(π/4)tanα)
⇒ tanθ = tan(α – π/4)
⇒ θ = (α – π/4)
Ahora tomando cos en ambos lados, obtenemos
⇒ cosθ = cos(α – π/4)
⇒ cosθ = cosα.cos(π/4) + sinα.sin(π/4)
⇒ cosθ = cosα(1/√2) + senα(1/√2)
⇒ cosθ = (cosα + senα)/√2
⇒ √2cosθ = senα + cosα
Por lo tanto probado
Pregunta 34. Si tan(A + B) = p, tan(A – B) = q, entonces demuestre que tan2A = (p + q)/(1 – pq)
Solución:
Dado que, tan(A + B) = p, tan(A – B) = q
Ahora resolvamos RHS,
(p + q)/(1 – pq) =
=
=
=
=
=
=
= tan2A = LHS
LHS = RHS
Por lo tanto Probado.
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA