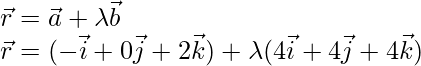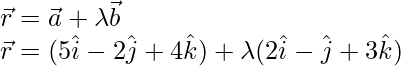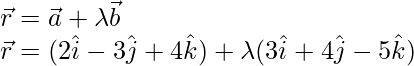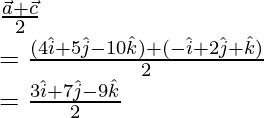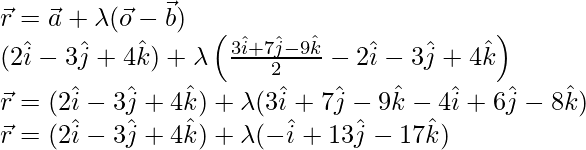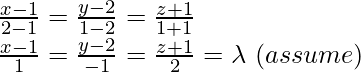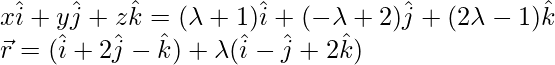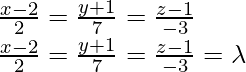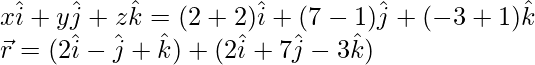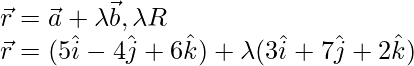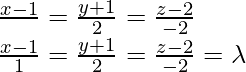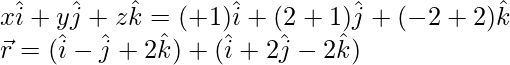Clase 12 Soluciones RD Sharma – Capítulo 28 La línea recta en el espacio – Ejercicio 28.1

Pregunta 1. Encuentra el vector y la ecuación cartesiana de la recta que pasa por los puntos (5, 2, -4) y que es paralela al vector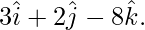 $3\hat{i}+2\hat{j}-8\hat{k}.$

Solución:

Como sabemos que la ecuación vectorial de una recta es;

$\vec{r}=\vec{a}+\lambda\vec{b}$

Así, la ecuación cartesiana de una recta es;

$\frac{x-x_1}{a_1}=\frac{y-y_1}{a_2}=\frac{x-x_3}{a_3}$

Después de aplicar las fórmulas anteriores;

La ecuación vectorial de la recta es;

$\vec{r}=(5\hat{i}+2\hat{j}-4\hat{k})+\lambda(3\hat{i}+2\hat{j}-8\hat{k})$

La ecuación cartesiana de una línea es;

$\frac{x-5}{3}=\frac{y-2}{2}=\frac{z+4}{-8}$

Pregunta 2. Encuentra la ecuación vectorial de la recta que pasa por los puntos (-1, 0, 2) y (3, 4, 6).

Solución:

Dado:

Aquí, las relaciones de dirección de la línea son;

(3 + 1, 4 – 0, 6 – 2) = (4, 4, 4)

Por tanto, la recta dada pasa por

(-1, 0, 2)

Como sabemos que la ecuación vectorial de una línea se da como;

$\vec{r}=\vec{a}+\lambda\vec{b}$

Así, valores sustitutivos

Por lo tanto, obtenemos

$\vec{r}=\vec{a}+\lambda\vec{b}\\ \vec{r}=(-\vec{i}+0\vec{j}+2\vec{k})+\lambda(4\vec{i}+4\vec{j}+4\vec{k})$

Por lo tanto,

La ecuación vectorial de la recta es;

$\vec{r}=(-\vec{i}+0\vec{j}+2\vec{k})+\lambda(4\vec{i}+4\vec{j}+4\vec{k})$

Cuestión 3. Fina la ecuación vectorial de una recta que es paralela al vector 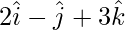$2\hat{i}-\hat{j}+3\hat{k}$ y que pasa por el punto (5, -2, 4), También redúcela a forma cartesiana.

Solución:

Considerar,

La ecuación vectorial de la línea que pasa por un punto fijo vector a y paralela al vector b se muestra como;

$\vec{r}=\vec{a}+\lambda\vec{b}$

Aquí, λ es escalar

$\vec{b}=2\hat{i}-\hat{j}+3\hat{k}$ y $\vec{a}=5\hat{i}-2\hat{j}+4\hat{k}$

La ecuación de la línea requerida es;

$\vec{r}=\vec{a}+\lambda\vec{b}\\ \vec{r}=(5\hat{i}-2\hat{j}+4\hat{k})+\lambda(2\hat{i}-\hat{j}+3\hat{k})$

Ahora sustituya el valor de r aquí

$\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$

Así, obtenemos

$(x\hat{i}+y\hat{j}+z\hat{k})=(5+2\lambda)\hat{i}+(-2-\lambda)\hat{j}+(4+3\lambda)\hat{k}$

Ahora compare los coeficientes del vector

x = 5 + 2λ,y = -2 – λ,z = 4 + 3λ

Después de igualar a λ,

Tendremos

$\frac{x-5}{2}=λ ,\ \ \frac{y+2}{-0}=λ ,\ \ \frac{z-4}{3}=λ$

Por lo tanto,

La forma cartesiana de ecuación de la recta es;

$\frac{x-5}{2} =\ \ \frac{y+2}{-0} =\ \ \frac{z-4}{3}$

Pregunta 4. Una línea que pasa por el punto con vector de posición 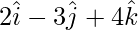$2\hat{i}-3\hat{j}+4\hat{k}$ y tiene la dirección de 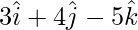$3\hat{i}+4\hat{j}-5\hat{k}$ . Encuentra ecuaciones de la recta en forma vectorial y cartesiana.

Solución:

Considerar,

La ecuación vectorial de la línea que pasa por un punto fijo vector a y paralela al vector b se muestra como;

$\vec{r}=\vec{a}+\lambda\vec{b}$

Aquí, λ es escalar

$\vec{a}=2\hat{i}-3\hat{j}+4\hat{k}$ y $\vec{b}=3\hat{i}+4\hat{j}-5\hat{k}$

La ecuación de la línea requerida es;

$\vec{r}=\vec{a}+\lambda\vec{b}\\ \vec{r}=(2\hat{i}-3\hat{j}+4\hat{k})+\lambda(3\hat{i}+4\hat{j}-5\hat{k})$

Ahora sustituya el valor de r aquí

$\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$

Así, obtenemos

$(x\hat{i}+y\hat{j}+z\hat{k})=(2+3\lambda)\hat{i}+(-3+4\lambda)\hat{j}+(4-5\lambda)\hat{k}$

Ahora compare los coeficientes del vector

x = 2 + 3λ,y = -3 + 4λ,z = 4 – 5λ

Después de igualar a λ,

Tendremos

$\frac{x-2}{3}=λ ,\ \ \frac{y+3}{4}=λ ,\ \ \frac{z-4}{-5}=λ$

Por lo tanto,

La forma cartesiana de ecuación de la recta es;

$\frac{x-2}{3} =\ \ \frac{y+3}{4} =\ \ \frac{z-4}{-5}$

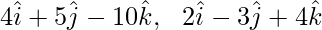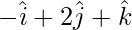Pregunta 5. ABCD es un paralelogramo. Los vectores de posición de los puntos A, B y C son respectivamente, $4\hat{i}+5\hat{j}-10\hat{k},\ \ 2\hat{i}-3\hat{j}+4\hat{k}$ y $-\hat{i}+2\hat{j}+\hat{k}$ . Encuentra la ecuación vectorial de la línea BD. También redúzcalo a la forma cartesiana.

Solución:

Dado: ABCD es un paralelogramo.

Considere: AC y BD se bisecan en el punto O.

De este modo,

Vector posición del punto O = $\frac{\vec{a}+\vec{c}}{2}\\ =\frac{(4\hat{i}+5\hat{j}-10\hat{k})+(-\hat{i}+2\hat{j}+\hat{k})}{2}\\ =\frac{3\hat{i}+7\hat{j}-9\hat{k}}{2}$

Ahora, considere que los vectores de posición del punto O y B están representados por

$\vec{o}$ y $\vec{b}$

De este modo,

La ecuación de la recta BD es la recta que pasa por O y B viene dada por

$\vec{r}=\vec{a}+\lambda(\vec{b}-\vec{a})$ [Puesto que la ecuación de la recta que pasa por dos puntos $\vec{a}$ y $\vec{b}$ ]

$\vec{r}=\vec{a}+\lambda(\vec{o}-\vec{b})\\ (2\hat{i}-3\hat{j}+4\hat{k})+\lambda\left(\frac{3\hat{i}+7\hat{j}-9\hat{k}}{2}-2\hat{i}-3\hat{j}+4\hat{k}\right)\\ \vec{r}=(2\hat{i}-3\hat{j}+4\hat{k})+\lambda(3\hat{i}+7\hat{j}-9\hat{k}-4\hat{i}+6\hat{j}-8\hat{k})\\ \vec{r}=(2\hat{i}-3\hat{j}+4\hat{k})+\lambda(-\hat{i}+13\hat{j}-17\hat{k})$

Ahora, compare los coeficientes del vector i, j, R

x = 2 – λ, y = -3 – 13λ, z = 4 – 17λ

Después de igualar a λ,

Tendremos

$\frac{x-2}{-1}=λ ,\ \ \frac{y+3}{13}=λ ,\ \ \frac{z-4}{-17}=λ$

Por lo tanto,

La forma cartesiana de ecuación de la recta es;

$\frac{x-2}{-1} =\ \ \frac{y+3}{13} =\ \ \frac{z-4}{-17}$

Pregunta 6. Halla en forma vectorial, así como en forma cartesiana, la ecuación de la recta que pasa por los puntos A(1, 2, -1) y B(2, 1, 1).

Solución:

Sabemos que la ecuación de la recta que pasa por dos puntos (x ₁ , y ₁ ,z ₁ ) y (x ₂ , y ₂ , z ₂ ) es

$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}\ \ \ \ \ \ \ ....(i)\\$

Aquí,

(x ₁ , y ₁ , z ₁ ) = A(1, 2, -1)

(x ₂ , y ₂ ,z ₂ ) = B(2, 1, 1)

Usando la ecuación (i), la ecuación de la línea AB,

$\frac{x-1}{2-1}=\frac{y-2}{1-2}=\frac{z+1}{1+1}\\ \frac{x-1}{1}=\frac{y-2}{-1}=\frac{z+1}{2}=\lambda\ (assume)$

x = λ + 1, y = -λ + 2, z = 2λ – 1

La forma vectorial de la ecuación de la línea AB es,

$x\hat{i}+y\hat{j}+z\hat{k}=(\lambda+1)\hat{i}+(-\lambda+2)\hat{j}+(2\lambda-1)\hat{k}\\ \vec{r}=(\hat{i}+2\hat{j}-\hat{k})+\lambda(\hat{i}-\hat{j}+2\hat{k})$

Pregunta 7. Encuentra la ecuación vectorial de la recta que pasa por el punto (1, 2, 3) y es paralela al vector 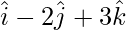$\hat{i}-2\hat{j}+3\hat{k}$ . Reducir la ecuación correspondiente en forma cartesiana.

Solución:

Sabemos que la ecuación vectorial de una recta que pasa por $\vec{a}$ el vector y es paralela al $\vec{b}$ mismo está dada por,

$\vec{r}=\vec{a}+\lambda\vec{b}$

Aquí,

$\vec{a}=\hat{i}+2\hat{j}+3\hat{k}$ y $\vec{b}=\hat{i}-2\hat{j}+3\hat{k}$

Entonces, la ecuación vectorial requerida de la línea es,

$\vec{r}=(\hat{i}+2\hat{j}+3\hat{k})+\lambda(\hat{i}-2\hat{j}+3\hat{k})$

Ahora,

$(x\hat{i}+y\hat{j}+z\hat{k})=(1+\lambda)\hat{i}+(2-2\lambda)\hat{j}+(3+3\lambda)\hat{k}$

Igualando los coeficientes de $\hat{i},\ \hat{j},\ \hat{k}$

x = 1 + λ, y = 2 – 2λ, z = 3 + 3λ

x – 1 = λ, $\frac{y-2}{2}=λ,\ \frac{z-3}{3}=λ$

Entonces, la ecuación requerida de la línea es la forma cartesiana,

$\frac{x-1}{1}=\frac{y-2}{-2}=\frac{z-3}{3}$

Pregunta 8. Encuentra la ecuación vectorial de una recta que pasa por (2, −1, 1) y es paralela a la recta cuyas ecuaciones son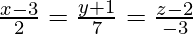 $\frac{x-3}{2}=\frac{y+1}{7}=\frac{z-2}{-3}$

Solución:

Sabemos que, la ecuación de una línea que pasa por un punto (x ₁ , y ₁ , z ₁ ) y que tiene relaciones de dirección proporcionales a a, b, c es

$\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}\ \ \ \ .....(i)$

Aquí,

(x ₁ , y ₁ , z ₁ ) = (2, -1, 1) y

La línea dada $\frac{x-3}{2}=\frac{y+1}{7}=\frac{z-2}{-3}$ es paralela a la línea requerida.

a = 2 μ, b = 7 μ, c = -3 μ

Entonces, la ecuación de la línea requerida usando la ecuación (i)

$\frac{x-2}{2μ }=\frac{y+1}{7μ }=\frac{z-1}{-3μ }\\ \frac{x-2}{2}=\frac{y+1}{7}=\frac{z-1}{-3}=\lambda$

x = 2λ + 2, y = 7λ – 1, z = -3λ + 1

Asi que,

$x\hat{i}+y\hat{j}+z\hat{k}=(2λ+2)\hat{i}+(7λ-1)\hat{j}+(-3λ+1)\hat{k}\\ \vec{r}=(2\hat{i}-\hat{j}+\hat{k})+λ(2\hat{i}+7\hat{j}-3\hat{k})$

Pregunta 9. La ecuación cartesiana de una recta es 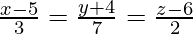$\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}$ . Escribe su forma vectorial

Solución:

La ecuación cartesiana de la recta es

$\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}$ ….(i)

La recta dada pasa por el punto (5, -4, 6). El vector de posición de este punto es

$\vec{a}=5\hat{i}-4\hat{j}+6\hat{k}$

Además, las relaciones de dirección de la línea dada son 3, 7 y 2.

Esto significa que la línea está en la dirección del vector,

$\vec{b}=3\hat{i}+7\hat{j}+2\hat{k}$

Se sabe que la línea que pasa por el vector de posición $\vec{a}$ y en la dirección del vector $\vec{b}$ está dada por la ecuación,

$\vec{r}=\vec{a}+\lambda \vec{b}, \lambda ∈R\\ \vec{r}=(5\hat{i}-4\hat{j}+6\hat{k})+\lambda(3\hat{i}+7\hat{j}+2\hat{k})$

Pregunta 10. Encuentra la ecuación cartesiana de una recta que pasa por (1, -1, 2) y es paralela a la recta cuyas ecuaciones son 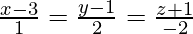$\frac{x-3}{1}=\frac{y-1}{2}=\frac{z+1}{-2}$ . Además, reduce la ecuación obtenida en forma vectorial.

Solución:

Sabemos que, la ecuación de una línea que pasa por un punto (x ₁ , y ₁ , z ₁ ) y que tiene relaciones de dirección proporcionales a a, b, c es

$\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}\ \ \ \ \ ......(i)$

Aquí,

(x ₁ , y ₁ , z ₁ ) = (1, -1, 2) y

La línea dada $\frac{x-3}{1}=\frac{y-1}{2}=\frac{z+1}{-2}$ es paralela a la línea requerida,

Asi que,

a = μ, b = 2 μ, c = -2 μ

Entonces, la ecuación de la línea requerida usando la ecuación (i) es,

$\frac{x-1}{μ }=\frac{y+1}{2μ }=\frac{z-2}{-2μ }\\ \frac{x-1}{1}=\frac{y+1}{2}=\frac{z-2}{-2}=\lambda$

x = λ + 1, y = 2λ – 1, z = -2λ +2

Asi que,

$x\hat{i}+y\hat{j}+z\hat{k}=(λ+1)\hat{i}+(2λ+1)\hat{j}+(-2λ+ 2)\hat{k}\\ \vec{r}=(\hat{i}-\hat{j}+2\hat{k})+λ(\hat{i}+2\hat{j}-2\hat{k})$

Publicación traducida automáticamente

Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones RD Sharma – Capítulo 28 La línea recta en el espacio – Ejercicio 28.1 | Serie 1

Pregunta 1. Encuentra el vector y la ecuación cartesiana de la recta que pasa por los puntos (5, 2, -4) y que es paralela al vector $3\hat{i}+2\hat{j}-8\hat{k}.$

Pregunta 2. Encuentra la ecuación vectorial de la recta que pasa por los puntos (-1, 0, 2) y (3, 4, 6).

Cuestión 3. Fina la ecuación vectorial de una recta que es paralela al vector $2\hat{i}-\hat{j}+3\hat{k}$ y que pasa por el punto (5, -2, 4), También redúcela a forma cartesiana.

Pregunta 4. Una línea que pasa por el punto con vector de posición $2\hat{i}-3\hat{j}+4\hat{k}$ y tiene la dirección de $3\hat{i}+4\hat{j}-5\hat{k}$ . Encuentra ecuaciones de la recta en forma vectorial y cartesiana.

Pregunta 5. ABCD es un paralelogramo. Los vectores de posición de los puntos A, B y C son respectivamente, $4\hat{i}+5\hat{j}-10\hat{k},\ \ 2\hat{i}-3\hat{j}+4\hat{k}$ y $-\hat{i}+2\hat{j}+\hat{k}$ . Encuentra la ecuación vectorial de la línea BD. También redúzcalo a la forma cartesiana.

Pregunta 6. Halla en forma vectorial, así como en forma cartesiana, la ecuación de la recta que pasa por los puntos A(1, 2, -1) y B(2, 1, 1).

Pregunta 7. Encuentra la ecuación vectorial de la recta que pasa por el punto (1, 2, 3) y es paralela al vector $\hat{i}-2\hat{j}+3\hat{k}$ . Reducir la ecuación correspondiente en forma cartesiana.

Pregunta 8. Encuentra la ecuación vectorial de una recta que pasa por (2, −1, 1) y es paralela a la recta cuyas ecuaciones son $\frac{x-3}{2}=\frac{y+1}{7}=\frac{z-2}{-3}$

Pregunta 9. La ecuación cartesiana de una recta es $\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}$ . Escribe su forma vectorial

Pregunta 10. Encuentra la ecuación cartesiana de una recta que pasa por (1, -1, 2) y es paralela a la recta cuyas ecuaciones son $\frac{x-3}{1}=\frac{y-1}{2}=\frac{z+1}{-2}$ . Además, reduce la ecuación obtenida en forma vectorial.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra el vector y la ecuación cartesiana de la recta que pasa por los puntos (5, 2, -4) y que es paralela al vector

Pregunta 2. Encuentra la ecuación vectorial de la recta que pasa por los puntos (-1, 0, 2) y (3, 4, 6).

Cuestión 3. Fina la ecuación vectorial de una recta que es paralela al vector y que pasa por el punto (5, -2, 4), También redúcela a forma cartesiana.

Pregunta 4. Una línea que pasa por el punto con vector de posición y tiene la dirección de . Encuentra ecuaciones de la recta en forma vectorial y cartesiana.

Pregunta 5. ABCD es un paralelogramo. Los vectores de posición de los puntos A, B y C son respectivamente, y . Encuentra la ecuación vectorial de la línea BD. También redúzcalo a la forma cartesiana.

Pregunta 6. Halla en forma vectorial, así como en forma cartesiana, la ecuación de la recta que pasa por los puntos A(1, 2, -1) y B(2, 1, 1).

Pregunta 7. Encuentra la ecuación vectorial de la recta que pasa por el punto (1, 2, 3) y es paralela al vector . Reducir la ecuación correspondiente en forma cartesiana.

Pregunta 8. Encuentra la ecuación vectorial de una recta que pasa por (2, −1, 1) y es paralela a la recta cuyas ecuaciones son

Pregunta 9. La ecuación cartesiana de una recta es . Escribe su forma vectorial

Pregunta 10. Encuentra la ecuación cartesiana de una recta que pasa por (1, -1, 2) y es paralela a la recta cuyas ecuaciones son . Además, reduce la ecuación obtenida en forma vectorial.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra el vector y la ecuación cartesiana de la recta que pasa por los puntos (5, 2, -4) y que es paralela al vector $3\hat{i}+2\hat{j}-8\hat{k}.$

Cuestión 3. Fina la ecuación vectorial de una recta que es paralela al vector $2\hat{i}-\hat{j}+3\hat{k}$ y que pasa por el punto (5, -2, 4), También redúcela a forma cartesiana.

Pregunta 4. Una línea que pasa por el punto con vector de posición $2\hat{i}-3\hat{j}+4\hat{k}$ y tiene la dirección de $3\hat{i}+4\hat{j}-5\hat{k}$ . Encuentra ecuaciones de la recta en forma vectorial y cartesiana.

Pregunta 5. ABCD es un paralelogramo. Los vectores de posición de los puntos A, B y C son respectivamente, $4\hat{i}+5\hat{j}-10\hat{k},\ \ 2\hat{i}-3\hat{j}+4\hat{k}$ y $-\hat{i}+2\hat{j}+\hat{k}$ . Encuentra la ecuación vectorial de la línea BD. También redúzcalo a la forma cartesiana.

Pregunta 7. Encuentra la ecuación vectorial de la recta que pasa por el punto (1, 2, 3) y es paralela al vector $\hat{i}-2\hat{j}+3\hat{k}$ . Reducir la ecuación correspondiente en forma cartesiana.

Pregunta 8. Encuentra la ecuación vectorial de una recta que pasa por (2, −1, 1) y es paralela a la recta cuyas ecuaciones son $\frac{x-3}{2}=\frac{y+1}{7}=\frac{z-2}{-3}$

Pregunta 9. La ecuación cartesiana de una recta es $\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}$ . Escribe su forma vectorial

Pregunta 10. Encuentra la ecuación cartesiana de una recta que pasa por (1, -1, 2) y es paralela a la recta cuyas ecuaciones son $\frac{x-3}{1}=\frac{y-1}{2}=\frac{z+1}{-2}$ . Además, reduce la ecuación obtenida en forma vectorial.