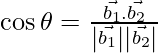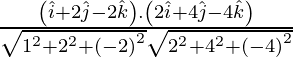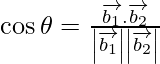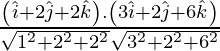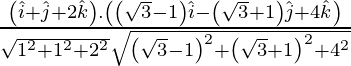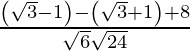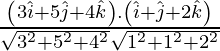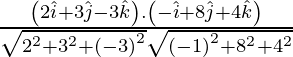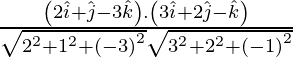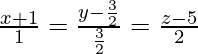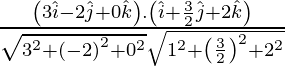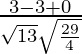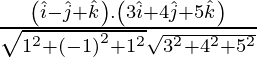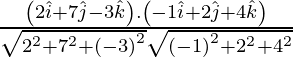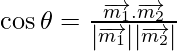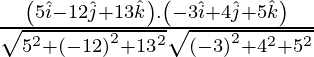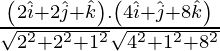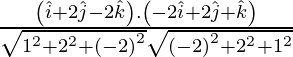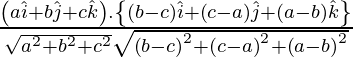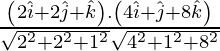Pregunta 1. Muestre que las tres rectas con cosenos directores 12/13, -3/13, – 4/13; 13/4, 13/12, 13/3; 3/13, – 4/13, 12/13 son mutuamente perpendiculares.
Solución:
Los cosenos directores de las tres rectas son
l 1 = 12/13, m 1 = -3/13, n 1 = -4/13
l 2 = 4/13, m 2 = 12/13, n 2 = 3/13
l 3 = 3/13, m 3 = -4/13, n 3 = 12/13
Entonces, l 1 l 2 + metro 1 metro 2 + norte 1 norte 2 =
= 0
También,
l 2 l 3 + metro 2 metro 3 + norte 2 norte 3 =
= 0
l 1 l 3 + metro 1 metro 3 + norte 1 norte 3 =
= 0
Por lo tanto, las rectas dadas son perpendiculares entre sí.
Por lo tanto probado.
Pregunta 2. Demuestra que la recta que pasa por los puntos (1, −1, 2) y (3, 4, −2) es perpendicular a la que pasa por los puntos (0, 3, 2) y (3, 5, 6).
Solución:
Tenemos,
pasa por los puntos (1, -1, 2) y (3, 4, -2).
Además,
está pasando por los puntos (0, 3, 2) y (3, 5, 6).
Después,
Ahora,
= 6 + 10 – 16
= 0
Por lo tanto, las rectas dadas son perpendiculares entre sí.
Por lo tanto probado.
Pregunta 3. Demuestra que la recta que pasa por los puntos (4, 7, 8) y (2, 3, 4) es paralela a la recta que pasa por los puntos (−1, −2, 1) y (1, 2, 5 ).
Solución:
Las ecuaciones de las rectas que pasan por los puntos (x 1 , y 1 , z 1 ) y (x 2 , y 2 , z 2 ) están dadas por
Entonces, la ecuación de una recta que pasa por (4, 7, 8) y (2, 3, 4) es
Además, la ecuación de la recta que pasa por los puntos (-1, -2,1) y (1, 2, 5) es
Sabemos que dos rectas son paralelas si,
Y las ecuaciones cartesianas de las dos rectas vienen dadas por,
Entonces, obtenemos,
Por lo tanto, las rectas dadas son paralelas entre sí.
Por lo tanto probado.
Pregunta 4. Encuentra la ecuación cartesiana de la recta que pasa por el punto (−2, 4, −5) y paralela a la recta dada por 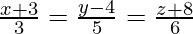 .
.
Solución:
Sabemos que la ecuación cartesiana de una recta que pasa por un punto con posición vectorial
y paralela al vector
está dada por,
Aquí,
La ecuación cartesiana de la línea requerida es,
=>
Pregunta 5. Demuestra que las rectas 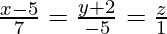 y
y 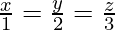 son perpendiculares entre sí.
son perpendiculares entre sí.
Solución:
Tenemos
Y también,
Estas ecuaciones se pueden reescribir como,
. . . . (1)
. . . . (2)
Por tanto, el vector paralelo a la recta (1) viene dado por,
Y el vector paralelo a la recta (2) viene dado por,
Ahora,
= 7 – 10 + 3
= 0
Por lo tanto, las dos rectas dadas son perpendiculares entre sí.
Por lo tanto probado.
Pregunta 6. Demuestra que la recta que une el origen con el punto (2, 1, 1) es perpendicular a la recta determinada por los puntos (3, 5, −1) y (4, 3, −1).
Solución:
Las razones de dirección de la línea que une el origen con el punto (2, 1, 1) son 2, 1, 1.
Dejar
Las razones de dirección de la línea que une los puntos (3, 5, -1) y (4, 3, -1) son 1, -2, 0.
Dejar
Ahora,
= 2 – 2 + 0
= 0
Entonces, obtenemos
.
Por tanto, las dos rectas que unen los puntos dados son perpendiculares entre sí.
Por lo tanto probado.
Pregunta 7. Encuentra la ecuación de una línea paralela al eje x y que pasa por el origen.
Solución:
Las relaciones de dirección de la línea paralela al eje x son proporcionales a 1, 0, 0.
La ecuación de la recta que pasa por el origen (0, 0, 0) y es paralela al eje x es
=>
Pregunta 8. Encuentra el ángulo entre el siguiente par de líneas:
(yo) ![]() y
y![]()
Solución:
Tenemos,
Y también,
Sean
y
vectores paralelos a las rectas dadas.
Ahora,
Si θ es el ángulo entre las rectas dadas, entonces
=
=
= 1
Como cos θ = 1
=> θ = 0°
Por lo tanto, el ángulo entre dos líneas es 0°.
(ii) ![]() y
y![]()
Solución:
Tenemos,
Y también,
Sean
y
vectores paralelos a las rectas dadas.
Ahora,
Si θ es el ángulo entre la línea dada, entonces
=
=
= 19/21
Como cos θ = 19/21
=> θ = cos -1 (19/21)
Por tanto, el ángulo entre dos rectas es cos -1 (19/21).
(iii) ![]() y
y![]()
Solución:
Tenemos,
Y también,
Sean
y
vectores paralelos a la recta dada.
Ahora,
Si θ es el ángulo entre la línea dada, entonces
=
=
= 6/12
= 1/2
Como cos θ = 1/2
=> θ = π/3
Por lo tanto, el ángulo entre dos rectas es π/3.
Pregunta 9. Encuentra el ángulo entre el siguiente par de líneas:
(yo) ![]() y
y ![]()
Solución:
Tenemos,
Y también,
Sean ,
y
vectores paralelos a la recta dada.
Si θ es el ángulo entre la línea dada, entonces
=
=
= 8/5√3
Como cos θ = 8/5√3
=> θ = cos -1 (8/5√3)
Por lo tanto, el ángulo entre dos rectas es cos -1 (8/5√3).
(ii) ![]() y
y![]()
Solución:
Tenemos,
Y también,
Sean
y
vectores paralelos a las rectas dadas.
Ahora,
Si θ es el ángulo entre las rectas dadas, entonces
=
=
=
Como cos θ =
=> θ =
Por lo tanto, el ángulo entre dos rectas es
.
(iii) ![]() y
y![]()
Solución:
Tenemos,
Y también,
La ecuación de la recta dada se puede reescribir como
Sean
y
vectores paralelos a las rectas dadas.
Ahora,
Si θ es el ángulo entre las rectas dadas, entonces
=
=
= 11/14
Como cos θ = 11/14
=> θ = cos -1 (11/14)
Por tanto, el ángulo entre dos rectas es cos -1 (11/14).
(iv) ![]() y
y![]()
Solución:
Tenemos,
Y también,
Las ecuaciones de las líneas dadas se pueden reescribir como
Sean
y
vectores paralelos a las rectas dadas.
Ahora,
Si θ es el ángulo entre las rectas dadas, entonces
=
=
= 0
Como cos θ = 0
=> θ = π/2
Por lo tanto, el ángulo entre dos rectas es π/2.
(v) ![]() y
y![]()
Solución:
Tenemos,
Y también,
Las ecuaciones de las líneas dadas se pueden reescribir como,
Sean
y
vectores paralelos a las rectas dadas.
Ahora,
Si θ es el ángulo entre las rectas dadas, entonces
=
=
= 4/5√6
Como cos θ = 4/5√6
=> θ = cos -1 (4/5√6)
Por lo tanto, el ángulo entre dos rectas es cos -1 (4/5√6).
(vi) ![]() y
y![]()
Solución:
Tenemos,
Y también,
Las ecuaciones de las líneas dadas se pueden reescribir como
Sean
y
vectores paralelos a las rectas dadas.
Ahora,
Si θ es el ángulo entre las rectas dadas, entonces
=
=
= 0
Como cos θ = 0
=> θ = π/2
Por lo tanto, el ángulo entre dos rectas es π/2.
Pregunta 10. Encuentra el ángulo entre los pares de líneas con relaciones de dirección proporcionales a:
(i) 5, −12, 13 y −3, 4, 5
Solución:
Tenemos pares de líneas con razones de dirección proporcionales a 5, −12, 13 y −3, 4, 5.
Sean
y
vectores paralelos a las dos rectas dadas.
Entonces, el ángulo entre las dos rectas dadas es igual al ángulo entre
y
.
Ahora,
El vector paralelo a la línea que tiene relaciones de dirección proporcionales a 5, – 12, 13 es,
Y el vector paralelo a la línea que tiene relaciones de dirección proporcionales a -3, 4, 5 es,
Sea θ el ángulo entre las rectas.
Ahora,
=
=
= 1/65
Como cos θ = 1/65
=> θ = cos -1 (1/65)
Por tanto, el ángulo entre dos rectas es cos -1 (1/65).
(ii) 2, 2, 1 y 4, 1, 8
Solución:
Tenemos pares de rectas con razones de dirección proporcionales a 2, 2, 1 y 4, 1, 8.
Sean
y
vectores paralelos a las dos rectas dadas.
Entonces, el ángulo entre las líneas es igual al ángulo entre
y
.
Ahora,
El vector paralelo a la línea que tiene relaciones de dirección proporcionales a 2, 2, 1 es,
Y el vector paralelo a la línea que tiene relaciones de dirección proporcionales a 4, 1, 8 es,
Sea θ el ángulo entre las rectas.
Ahora,
=
=
= 2/3
Como cos θ = 2/3
=> θ = cos -1 (2/3)
Por tanto, el ángulo entre dos rectas es cos -1 (2/3).
(iii) 1, 2, −2 y −2, 2, 1
Solución:
Tenemos pares de líneas con razones de dirección proporcionales a 1, 2, −2 y −2, 2, 1.
Sean
y
vectores paralelos a las dos rectas dadas.
Entonces, el ángulo entre las dos rectas dadas es igual al ángulo entre
y
.
Ahora,
El vector paralelo a la línea que tiene relaciones de dirección proporcionales a 1, 2, – 2 es,
Y el vector paralelo a la línea que tiene relaciones de dirección proporcionales a -2, 2, 1 es,
Sea θ el ángulo entre las rectas.
Ahora,
=
=
= 0
Como cos θ = 0
=> θ = π/2
Por lo tanto, el ángulo entre dos rectas es π/2.
(iv) a, b, c y b − c, c − a, a − b
Solución:
Tenemos pares de líneas con razones de dirección proporcionales a a, b, c y b − c, c − a, a − b.
Sean
y
vectores paralelos a las dos rectas dadas.
Entonces, el ángulo entre las dos líneas es igual al ángulo entre
y
.
Ahora,
El vector paralelo a la línea que tiene relaciones de dirección proporcionales a a, b, c es,
Y el vector paralelo a la línea que tiene relaciones de dirección proporcionales a b – c, c – a, a – b es,
Sea θ el ángulo entre las rectas.
Ahora,
=
=
= 0
Como cos θ = 0
=> θ = π/2
Por lo tanto, el ángulo entre dos rectas es π/2.
Pregunta 11. Encuentra el ángulo entre dos rectas, una de las cuales tiene relaciones de dirección 2, 2, 1 mientras que la otra se obtiene uniendo los puntos (3, 1, 4) y (7, 2, 12).
Solución:
Las razones de dirección de la línea que une los puntos (3, 1, 4) y (7, 2, 12) son proporcionales a 4, 1, 8.
Sean
y
vectores paralelos a las rectas que tienen relaciones de dirección proporcionales a 2, 2, 1 y 4, 1, 8.
Ahora,
Si θ es el ángulo entre las rectas dadas, entonces
=
=
= 2/3
Como cos θ = 2/3
=> θ = cos -1 (2/3)
Por tanto, el ángulo entre dos rectas es cos -1 (2/3).
Pregunta 12. Encuentra la ecuación de la recta que pasa por el punto (1, 2, −4) y es paralela a la recta 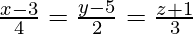 .
.
Solución:
Las relaciones de dirección de la línea paralela a la línea
son proporcionales a 4, 2, 3.
La ecuación de la línea requerida que pasa por el punto (1, 2,-4) que tiene relaciones de dirección proporcionales a 4, 2, 3 es
=>
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA