Integre las siguientes integrales:
Pregunta 1. ∫sen4x cos7x dx
Solución:
Sea yo =
Sabemos,
Aplicando esta fórmula a la pregunta dada obtenemos
yo=
=
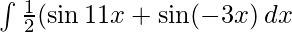
=
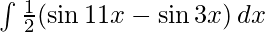
=
Sabemos,
Aplicando esta fórmula a la pregunta dada obtenemos
yo=
yo=
Pregunta 2. ∫ cos3x cos4x dx
Solución:
Sea yo =
Multiplicando y dividiendo la ecuación por 2, obtenemos
yo=
Sabemos,
Aplicando esta fórmula a la pregunta dada obtenemos
yo=
=
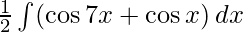
Sabemos,
y
Aplicando estas fórmulas a la pregunta dada obtenemos
yo=
yo=
Pregunta 3. ∫
Solución:
Sea yo =
Multiplicando y dividiendo la ecuación por 2, obtenemos
yo=
Sabemos,
Aplicando esta fórmula a la pregunta dada obtenemos
yo=
Sabemos,
Aplicando estas fórmulas a la pregunta dada obtenemos
yo=
Pregunta 4.
Solución:
Sea yo =
Multiplicando y dividiendo la ecuación por 2, obtenemos
yo=
Sabemos,
Aplicando esta fórmula a la pregunta dada obtenemos
yo=
Sabemos,
Aplicando estas fórmulas a la pregunta dada obtenemos
yo=
Publicación traducida automáticamente
Artículo escrito por manandeep1610 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA