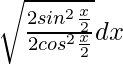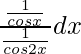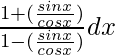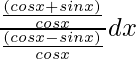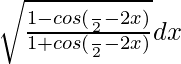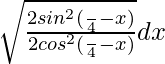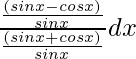Pregunta 1. Evalúa ∫ 1/√1 – cos2x dx
Solución:
Supongamos que I = ∫ 1/√1 – cos2x dx
∫ 1/√1 – cos2x dx = ∫1/√2sen 2 x dx
= ∫ 1/(√2 senx) dx
= (1/√2) ∫ cosec x dx
Integrar la ecuación anterior entonces obtenemos
= (1/√2) log|tan x/2| +c
Por lo tanto, I = (1/√2) log|tan x/2| +c
Pregunta 2. Evalúa ∫ 1/√1 + cos2x dx
Solución:
Supongamos que I = ∫ 1/√1 + cos2x dx
∫ 1/√1 + cos2x dx = ∫1/√2cos 2 x/2 dx
= ∫ 1/(√2 cosx/2) dx
= (1/√2) ∫ seg x/2 dx
= (1/√2) ∫ cosec (π/2 + x/2) dx
Integrar la ecuación anterior entonces obtenemos
= (2/√2) log|tan (π/4 + x/4| + c
Por lo tanto, I = √2 log|tan (π/4 + x/4| + c
Pregunta 3. Evaluar 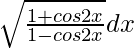
Solución:
Supongamos que yo =
= ∫ √(2 cos 2 x/2 sen 2 x) dx
= ∫ √cot 2 x dx
= ∫ cox dx
Integrar la ecuación anterior entonces obtenemos
= log|senx| + c [∫ cotx dx = log|senx| +c]
Por lo tanto, I = log|senx| +c
Pregunta 4. Evaluar 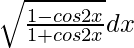
Solución:
Supongamos que yo =
=
= ∫ √tan 2 x/2 dx
= ∫ tanx/2 dx
Integrar la ecuación anterior entonces obtenemos
= -2log|cosx/2| + c [∫ tanx dx = – log|cosx| +c]
Por lo tanto, I = -2log|cosx/2| +c
Pregunta 5. Evalúa ∫secx/sec2x dx
Solución:
Supongamos que I = ∫secx/sec2x dx
∫segx/seg2x dx
=
= ∫cos2x/cosx dx
=
=
= ∫ 2cosx dx – ∫ secx dx
= 2∫ cosx dx – ∫ secx dx
Integrar la ecuación anterior entonces obtenemos
= 2senx – log|secx + tanx| +c
Por lo tanto, I = 2senx – log|secx + tanx| +c
Pregunta 6. Evalúa ∫ cos2x/(cosx + senx) 2 dx
Solución:
Supongamos que I = ∫ cos2x/(cosx + senx) 2 dx
∫ cos2x/(cosx + senx) 2 dx
=
= ∫ cos2x/(1 + sen2x) dx ………….(i)
Pon 1 + sen2x = t
2cos2x dx = dt
Ponga todos estos valores en la ecuación (i) entonces, obtenemos
= 1/2 ∫ 1/t dt
Integrar la ecuación anterior entonces obtenemos
= 1/2 registro|t| +c
= 1/2 log|1 + sen2x| +c
= 1/2 log|(cosx + senx) 2 | +c
Por lo tanto, I = log|senx + cosx| +c
Pregunta 7. Evalúa ∫ sin(x – a)/sin(x – b) dx
Solución:
Supongamos que I = ∫ sin(x – a)/sin(x – b) dx
∫ sin(x – a)/sin(x – b) dx = ∫ sin(x – a + b – b)/sin(x – b) dx
= ∫ sen(x – b + b – a)/sen(x – b) dx
=
=
= ∫ cos(b – a) dx + ∫ cot(x – b)sen(b – a) dx
= cos(b – a) ∫dx + sin(b – a)∫ cot(x – b) dx
Integrar la ecuación anterior entonces obtenemos
= xcos(b – a) + sen(b – a) log|sen(x – b)| +c
Por lo tanto, I = xcos(b – a) + sin(b – a) log|sin(x – b)| +c
Pregunta 8. Evalúa ∫ sin(x – a)/sin(x + a) dx
Solución:
Supongamos que I = ∫ sin(x – a)/sin(x + a) dx
∫ sin(x – a)/sin(x + a) dx = ∫ sin(x – a + a – a)/sin(x + a) dx
= ∫ sin(x + a – 2a)/sin(x + a) dx
=
=
= ∫ cos(2a) dx – ∫ cot(x+a)sen(2a) dx
= cos(2a) ∫dx + sin(2a)∫ cot(x+a) dx
Integrar la ecuación anterior entonces obtenemos
xcos(2a) + sen(2a) log|sen(x + a)| +c
Por lo tanto, I = xcos(2a) + sin(2a) log|sin(x + a)| +c
Pregunta 9. Evalúa ∫ 1 + tanx/1 – tanx dx
Solución:
Supongamos que I = ∫ 1 + tanx/1 – tanx dx
∫ 1 + tanx/1 – tanx dx
=
=
= ∫ (cosx + senx) / (cosx – senx) dx ………….(i)
Poner cosx – senx dx = t
(-senx – cosx) dx = dt
– (senx + cosx) dx = dt
dx = – dt/(senx + cosx)
Ponga todos estos valores en la ecuación (i), obtenemos
= – ∫dt/t
Integrar la ecuación anterior entonces obtenemos
= – registro|t| +c
= – log|cosx – senx| +c
Por lo tanto, I = – log|cosx – senx| +c
Pregunta 10. Evalúa ∫ cosx/cos(x – a) dx
Solución:
Supongamos que I = ∫ cosx/cos(x – a) dx
∫ cosx/cos(x – a) dx = ∫ cos(x + a – a)/cos(x – a) dx
= ∫ [cos(x – a)cosa – sen(x – a)sina]/cos(x – a) dx
= ∫ [cos(x – a)cosa]/cos(x – a) dx – ∫ [sen(x – a)sina]/cos(x – a) dx
= ∫ cosa dx – ∫ tan(x – a)sina dx
= cosa ∫dx – sina∫ tan(x – a) dx
Integrar la ecuación anterior entonces obtenemos
= x cosa – sina log|sec(x – a)| +c
Por tanto, I = x cosa – sina log|sec(x – a)| +c
Pregunta 11. Evaluar 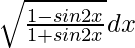
Solución:
Supongamos que yo =
=
=
= ∫ √tan 2 (π/4 – x) dx
= ∫ tan(π/4 – x) dx
Integrar la ecuación anterior entonces obtenemos
= log|cos(π/4 – x)| +c
Por lo tanto, I = log|cos(π/4 – x)| +c
Pregunta 12. Evalúa ∫ e 3x /(e 3x + 1) dx
Solución:
Supongamos que I = ∫ e 3x /(e 3x + 1) dx ………..(i)
Ponga e 3x + 1 = t, entonces
3e 3x dx = dt
dx = dt/3e 3x
Ponga todos estos valores en la ecuación (i), obtenemos
= 1/3 ∫dt/t
Integrando la ecuación anterior, obtenemos
= 1/3 registro|t| +c
= 1/3 registro |3e 3x + 1| +c
Por lo tanto, I = 1/3 log |3e 3x + 1| +c
Pregunta 13. Evalúa ∫ secxtanx/3secx + 5 dx
Solución:
Supongamos que I = ∫ secxtanx/3secx + 5 dx ………..(i)
Poner 3secx + 5 = t
3segxtanx dx = dt
dx = dt/3segxtanx
Ponga todos estos valores en la ecuación (i), obtenemos
= 1/3 ∫ dt/t
Integrando la ecuación anterior, obtenemos
= 1/3 registro|t| +c
= 1/3 log|3segx + 5| +c
Por lo tanto, I = 1/3 log|3secx + 5| +c
Pregunta 14. Evalúa ∫ 1 – cotx/1 + cotx dx
Solución:
Supongamos que I = ∫ 1 – cotx/1 + cotx dx
=
=
=
………..(yo)
Poner senx + cosx = t
cosx – senx dx = dt
-(senx – cosx) dx = dt
– dx = dt/senx – cosx
Ponga todos estos valores en la ecuación (i), obtenemos
= ∫ – dt/t
Integrando la ecuación anterior, obtenemos
= – registro|t| +c
= – log|senx + cosx| +c
Por lo tanto, I = – log|senx + cosx| +c
Pregunta 15. Evalúa ∫ secxcosecx/log(tanx) dx
Solución:
Supongamos que I = ∫ secxcosecx/log(tanx) dx ………..(i)
log(tanx) = t
secxcosecx dx = dt
Ponga todos estos valores en la ecuación (i), obtenemos
= ∫ dt/t
Integrando la ecuación anterior, obtenemos
= registro|t| +c
= log|log(tanx)| +c
Por lo tanto, I = log|log(tanx)| +c
Pregunta 16. Evalúa ∫1/ x(3+logx) dx
Solución:
Supongamos que I = ∫1/ x(3+logx) dx ………..(i)
Sea 3 + logx = t
d(3 + log x) = dt
\1/x dx = dt
dx = x dt
Poniendo 3 + logx =t y dx = xdt en la ecuación (i), obtenemos,
= ∫ dt/t
Integrando la ecuación anterior, obtenemos
= registro |t| +c
= registro|(3 + registro x)| +c
Por lo tanto, I = log|(3 + log x)| +c
Pregunta 17. Evalúa ∫ e x + 1 / e x + x dx
Solución:
Supongamos que I = ∫ e x + 1 / e x + x dx ………..(i)
Sea e x + x = t
d(ex + x ) = dt
(ex + 1) dx = dt
Ponga todos estos valores en la ecuación (i), obtenemos
= ∫ dt/t
Integrando la ecuación anterior, obtenemos
= registro |t| +c
= log|e x + x| +c
Por lo tanto, I = log|e x + x| +c
Pregunta 18. Evalúa ∫1/ (xlogx) dx
Solución:
Supongamos que I = ∫1/(xlogx) dx ………..(i)
Sea logx = t
d(log x) = dt
1/x dx = dt
dx = x dt
Ponga todos estos valores en la ecuación (i), obtenemos
= ∫ dt/t
Integrando la ecuación anterior, obtenemos
= registro |t| +c
= registro|(registro x)| +c
Por lo tanto, I = log|(log x)| +c
Pregunta 19. Evalúa ∫ sen2x/ (acos 2 x + bsen 2 x) dx
Solución:
Supongamos que I = ∫ sen2x/ (acos 2 x + bsen 2 x) dx ………..(i)
Sea acos 2 x + bsen 2 x = t
Al diferenciar ambos lados con respecto a x, obtenemos
d(acos 2 x + bsen 2 x) = dt
[a(2 cosx (-senx)) + b(2senxcosx)] dx = dt
[ -a (2 cosx senx) + b(2 senx cosx)] dx = dt
[ -a sen2x + bsen2x] dx = dt
sen2x (-a + b) dx = dt
sen2x (b – a) dx = dt
sen2x dx = dt/(b – a)
Ponga todos estos valores en la ecuación (i), obtenemos
= 1/(b – a) ∫ dt/t
Integrando la ecuación anterior, obtenemos
= 1/(b – a) registro |t| +c
= 1/(b – a) log|acos 2 x + bsen 2 x| +c
Por tanto, I = 1/(b – a) log|acos 2 x + bsen 2 x| +c
Pregunta 20. Evalúa ∫ cosx/ 2 + 3senx dx
Solución:
Supongamos que I = ∫ cosx/ 2 + 3senx dx ………..(i)
Sea 2 + 3senx = t
d(2 + 3senx) = dt
3cosx dx = dt
cosx dx = dt/3
Ponga todos estos valores en la ecuación (i), obtenemos
= 1/3 ∫ dt/t
Integrando la ecuación anterior, obtenemos
= 1/3 registro |t| +c
= 1/3 log|2 + 3senx| +c
Por lo tanto, I = 1/3 log|2 + 3senx| +c
Pregunta 21. Evalúa ∫ 1 – senx/ x + cosx dx
Solución:
Supongamos que I = ∫ 1 – senx/ x + cosx dx ………..(i)
Sea x + cosx = t
d(x + cosx) = dt
(1 – senx) dx = dt
Ponga todos estos valores en la ecuación (i), obtenemos
= ∫ dt/t
Integrando la ecuación anterior, obtenemos
= registro|t| +c
= log|x + cosx| +c
Por lo tanto, I = log|x + cosx| +c
Pregunta 22. Evalúa ∫ a/ b + ce x dx
Solución:
Supongamos que I = ∫ a/ b + ce x dx
=
= ∫ a/ e x (ser -x +c) dx ………..(i)
Sea -x + c = t
d(ser -x + c) = dt
-ser -x dx = dt
-b/e x dx = dt
1/e x dx = -dt/b
Ponga todos estos valores en la ecuación (i), obtenemos
= -a/b ∫ dt/t
Integrando la ecuación anterior, obtenemos
= -a/b registro|t| +c
= -a/b log|ser -x + c| +c
Por lo tanto, I = -a/b log|be -x + c| +c
Pregunta 23. Evalúa ∫ 1/ e x + 1 dx
Solución:
Supongamos que I = ∫ 1/ e x + 1 dx
=
= ∫ 1/ e x [1 + e -x ] dx ………..(i)
Sea 1 + e -x = t
d(1 + e -x ) = dt
-e -x dx = dt
1/e x dx = -dt
Ponga todos estos valores en la ecuación (i), obtenemos
= -∫ dt/t
Integrando la ecuación anterior, obtenemos
= -log|t| +c
= -log|1 + e -x | +c
Por lo tanto, I = -log|1 + e -x | +c
Pregunta 24. Evalúa ∫ cotx/logsinx dx
Solución:
Supongamos que I = ∫ cotx/logsinx dx ………..(i)
Sea logsinx = t
d(logsinx) = dt
cosx/senx dx = dt
cox dx = dt
Ponga todos estos valores en la ecuación (i), obtenemos
= ∫ dt/t
Integrando la ecuación anterior, obtenemos
= registro|t| +c
= log|log senx| +c
Por lo tanto, I = log|log senx| +c
Pregunta 25. Evalúa ∫ e 2x / e 2x – 2 dx
Solución:
Supongamos que I = ∫ e 2x / e 2x – 2 dx ………..(i)
Sea e 2x – 2 = t
d(e 2x – 2) = dt
e 2x dx = dt
Ponga todos estos valores en la ecuación (i), obtenemos
= 1/2 ∫ dt/t
Integrando la ecuación anterior, obtenemos
= 1/2 registro|t| +c
= 1/2 log|e 2x – 2| +c
Por lo tanto, I = 1/2 log|e 2x – 2| +c