Evalúe las siguientes integrales definidas:
Pregunta 23. 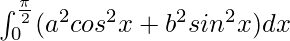
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo = [(a 2 + b 2 )/2][π/2]
yo = π(a 2 + b 2 )/4
Por lo tanto, el valor de
es π(a 2 + b 2 )/4.
Pregunta 24. 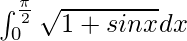
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo = 2[senπ/4 – cosπ/4 – 0 + 1]
Yo = 2[1/√2 – 1/√2 – 0 + 1]
yo = 2 (1)
yo = 2
Por lo tanto, el valor de
es 2.
Pregunta 25. 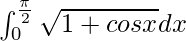
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo = 2√2[senπ/4 – sen0]
yo = 2√2[1/√2- sen0]
yo = 2√2[1/√2]
yo = 2
Por lo tanto, el valor de
es 2.
Pregunta 26. 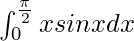
Solución:
Tenemos,
yo =
Al usar la integración por partes, obtenemos,
yo = x ∫senxdx – ∫(∫sen x (1)dx)dx
yo = -xcosx – ∫(∫sen xdx)dx
yo = -xcosx + ∫cosxdx
I = -xcosx + senx
Entonces obtenemos,
yo =
yo = [-π/2cosπ/2 + senπ/2 + 0 – 0]
yo = 0 + 1 + 0 – 0
yo = 1
Por lo tanto, el valor de
es 1.
Pregunta 27. 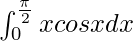
Solución:
Tenemos,
yo =
Al usar la integración por partes, obtenemos,
yo = x∫cosxdx – ∫(∫cos x (1)dx)dx
yo = xsenx – ∫(∫cosxdx)dx
I = xsenx – ∫senxdx
I = x sen x + cos x
Entonces obtenemos,
yo =
yo = [π/2senπ/2 + cosπ/2 – 0 – cos0]
yo = π/2 + 0 – 0 – 1
yo = π/2 – 1
Por lo tanto, el valor de
es π/2 – 1.
Pregunta 28. 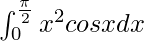
Solución:
Tenemos,
yo =
Al usar la integración por partes, obtenemos,
yo = x 2 senx – ∫(2x∫(cosx)dx)dx
yo = x 2 senx – ∫(2xsenx)dx
yo = x 2 senx – 2[-xcosx – ∫(1∫sinxdx)dx]
I = x 2 senx – 2[-xcosx + ∫sinxdx]
I = x 2 senx – 2[-xcosx + senx]
yo = x 2 senx + 2xcosx – 2senx
Entonces obtenemos,
yo =
yo = [(π/2) 2 sinπ/2 + 2(π/2)cosπ/2 – 2sinπ/2 – 0 – 0 + sin0]
yo = [π 2 /4 + 0 – 2 – 0 – 0 + 0]
yo = π 2 /4 – 2
Por lo tanto, el valor de
es π 2 /4 – 2.
Pregunta 29. 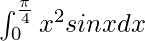
Solución:
Tenemos,
yo =
Al usar la integración por partes, obtenemos,
yo = -x 2 cosx – ∫(2x∫senxdx)dx
yo = -x 2 cosx + ∫(2xcosx)dx
yo = -x 2 cosx + 2[xsenx – ∫(∫cosxdx)dx]
I = -x 2 cosx + 2[xsenx – ∫senxdx]
I = -x 2 cosx + 2[xsenx + cosx]
yo = -x 2 cosx + 2xsenx + 2cosx
Entonces obtenemos,
yo =
yo = -(4) 2 cos4 + 2π/4senπ/4 + 2cosπ/4 + 0 – 0 – 2
yo = – 2 16(1/√2) + π/2(1/√2) + 2(1/√2) + 0 – 0 – 2
yo = – 2 16√2 + π/2√2 + √2 – 2
Por lo tanto, el valor de
es -π 2 /16√2 + π/2√2 + √2 – 2.
Pregunta 30. 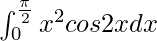
Solución:
Tenemos,
yo =
Al usar la integración por partes, obtenemos,
yo = 1/2x 2 sen2x – ∫(2x∫cos2xdx)dx
yo = 1/2x 2 sen2x – ∫(xsen2x)dx
yo = 1/2x 2 sen2x – [-1/2xcos2x – ∫(∫sen2xdx)dx]
I = 1/2x 2 sen2x – [-1/2xcos2x + ∫1/2 cos2xdx]
I = 1/2x 2 sen2x – [-1/2xcos2x + 1/4sen2xdx]
yo = 1/2x 2 sen2x + 1/2xcos2x – 1/4sen2xdx
Entonces obtenemos,
yo =
yo = [1/2(π 2 /4)senπ + 1/2(π/2)cosπ – 0 – 0 – 0 + 0]
yo = -π/4
Por lo tanto, el valor de
es -π/4.
Pregunta 31. 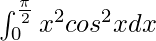
Solución:
Tenemos,
yo =
yo =
yo =
yo =
Al usar la integración por partes, obtenemos,
I = 1/2[x 3 /3] + x 2 sin2x/2 – [x ∫sin2x – ∫(∫sin2xdx)dx]
I = 1/2[x 3 /3] + x 2 sen2x/2 + xcosx/2 – sen2x/4
Entonces obtenemos,
yo =
yo = [1/6[π 3/8 ] + 0 + 0 – π/8]
yo = π 3/48 – π/8
Por lo tanto, el valor de
es π 3/48 – π/8.
Pregunta 32. 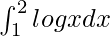
Solución:
Tenemos,
yo =
Al usar la integración por partes, obtenemos,
yo =
yo = xlogx – ∫1dx
yo = xlogx – x
Entonces obtenemos,
yo =
I = 2log2 – 2 – log1 + 1
I = 2 log 2 – 1
Por lo tanto, el valor de
es 2 log 2 – 1.
Pregunta 33. 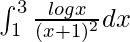
Solución:
Tenemos,
yo =
Al usar la integración por partes, obtenemos,
yo =
yo =
yo =
yo =
Entonces obtenemos,
yo =
I = -log3/4 + log3 – log4 + log1/2 – log1 + log2
I = log3(1 – 1/4) – 2log2 + 0 – 0 + log2
I = 3/4 log3 – log2
Por lo tanto, el valor de
es 3/4log3 – log2.
Pregunta 34. 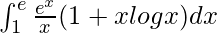
Solución:
Tenemos,
yo =
yo =
yo =
Al usar la integración por partes, obtenemos,
yo =
yo = e x logx
Entonces obtenemos,
yo =
I = e e loge – e 1 log1
yo = mi mi ( 1) – 0
yo = mi
Por lo tanto, el valor de
es e e .
Pregunta 35. 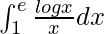
Solución:
Tenemos,
yo =
Sea log x = t, entonces tenemos,
=> (1/x) dx = dt
Ahora, el límite inferior es, x = 1
=> t = log x
=> t = registro 1
=> t = 0
Además, el límite superior es, x = e
=> t = log x
=> t = log e
=> t = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo = 1/2 – 0/2
yo = 1/2
Por lo tanto, el valor de
es 1/2.
Pregunta 36. 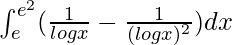
Solución:
Tenemos,
yo =
yo =
Al usar la integración por partes, obtenemos,
yo =
yo =
yo =
yo = x/logx
Entonces obtenemos,
yo =
yo =
yo =
yo = mi 2 /2 – mi
Por lo tanto, el valor de
es e 2 /2 – e.
Pregunta 37. 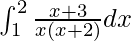
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
I = 1/2[3log2 – log4 + log3]
I = 1/2[3log2 – 2log2 + log3]
I = 1/2[registro 2 – registro 3]
yo = 1/2[log6]
yo = log6/2
Por lo tanto, el valor de
es log6/2.
Pregunta 38. 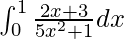
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
I = [1/5log6 + 3/√5tan -1 (√5) – 1/5log1 – 3/√5tan -1 (0)]
Yo = [1/5 log6 + 3√5 tan -1 (√5) – 0 – 0]
yo = 1/5 log6 + 3√5 tan -1 (√5)
Por lo tanto, el valor de
es 1/5 log6 + 3√5 tan -1 (√5).
Pregunta 39. 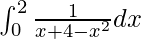
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
Sea x – 1/2 = t, entonces tenemos,
=> dx = dt
Ahora, el límite inferior es, x = 0
=> t = x – 1/2
=> t = 0 – 1/2
=> t = 1/2
Además, el límite superior es, x = 2
=> t = x – 1/2
=> t = 2 – 1/2
=> t = 3/2
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 40. 
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Yo = 4/2√7[tan -1 (5/√7) – tan -1 (1/√7)]
Yo = 2/√7[tan -1 (5/√7) – tan -1 (1/√7)]
Por lo tanto, el valor de
es 2/√7[tan -1 (5/√7) – tan -1 (1/√7)].
Pregunta 41. 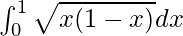
Solución:
Tenemos,
yo =
Sea x = sen 2 t, entonces tenemos,
=> dx = 2 sen t cos t dt
Ahora, el límite inferior es, x = 0
=> sen 2 t = 0
=> sen t = 0
=> t = 0
Además, el límite superior es, x = 1
=> sen 2 t = 1
=> sen t = 1
=> t = π/2
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Yo = 1/4[π/2 – 0] – 1/16[sen2π – 0]
Yo = 1/4[π/2] – 1/16[0 – 0 ]
yo = π/8
Por lo tanto, el valor de
es π/8.
Pregunta 42. 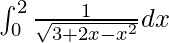
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
I = [sin -1 (1/2) – sin -1 (-1/2)]
yo = π/6 -(-π/6)
yo = π/6 + π/6
yo = π/3
Por lo tanto, el valor de
es π/3 .
Pregunta 43. ![]()
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
I = [sin -1 (2/2) – sin -1 (-2/2)]
I = sen -1 1 – sen -1 (-1)
yo = π/2 – (-π/2)
yo = π/2 + π/2
yo = π
Por lo tanto, el valor de
es π.
Pregunta 44. 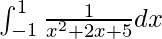
Solución:
Tenemos,
yo =
yo =
yo =
Sea x + 1 = t, entonces tenemos,
=> dx = dt
Ahora, el límite inferior es, x = –1
=> t = x + 1
=> t = – 1 + 1
=> t = 0
Además, el límite superior es, x = 1
=> t = x + 1
=> t = 1 + 1
=> t = 2
Entonces, la ecuación se convierte en,
yo =
yo =
I = 1/2 bronceado -1 2/2 – 1/2 bronceado -1 0/2
I = 1/2 bronceado -1 1 – 1/2 bronceado -1 0
yo = 1/2(π/4) – 0
yo = π/8
Por lo tanto, el valor de
es π/8.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
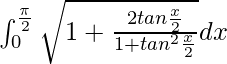
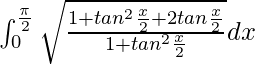
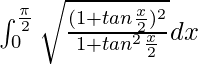
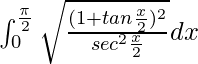
![Rendered by QuickLaTeX.com \left[\frac{1}{2}[\frac{x^3}{3}]+\frac{x^2sin2x}{2}+\frac{xcosx}{2}-\frac{sin2x}{4}\right]^{\frac{\pi}{2}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b3bbb3879a9d263c0ab554cf48cd640a_l3.png)
![Rendered by QuickLaTeX.com \left[-\frac{logx}{x+1}+logx - log(x+1)\right]^3_1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-92eb41692f3ce1a9f4a1fac71725c4b4_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{t^2}{2}\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2c5e346021330c4a8ef2df592857430d_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{x}{logx}\right]^{e^2}_e](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c41bee9ad48fab71e4ef0cd7571b6d82_l3.png)
![Rendered by QuickLaTeX.com \frac{1}{5}\left[log(5x^2+1)\right]^1_0+\left[\frac{3}{5}(\frac{1}{\frac{1}{\sqrt{5}}})tan^{-1}\frac{x}{\frac{1}{\sqrt{5}}}\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0f228b21737ca59dc90cee0b755569e6_l3.png)
![Rendered by QuickLaTeX.com \frac{1}{5}\left[log(5x^2+1)\right]^1_0+\left[\frac{3}{\sqrt{5}}tan^{-1}\sqrt{5}x\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-35cc75fa111655ca12bf3afc44ef1b81_l3.png)
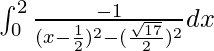
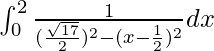
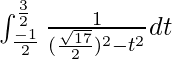
![Rendered by QuickLaTeX.com \left[\frac{1}{2(\frac{\sqrt{17}}{2})}log\frac{\frac{\sqrt{17}}{2}+t}{\frac{\sqrt{17}}{2}-t}\right]^{\frac{3}{2}}_{\frac{-1}{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-562ac3f9c240f5a66e18fc5243d23a61_l3.png)
![Rendered by QuickLaTeX.com \frac{1}{\sqrt{17}}\left[log\frac{\frac{\sqrt{17}}{2}+\frac{3}{2}}{\frac{\sqrt{17}}{2}-\frac{3}{2}}-log\frac{\frac{\sqrt{17}}{2}-\frac{1}{2}}{\frac{\sqrt{17}}{2}+\frac{1}{2}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-49669824fd492bd39218be251feda718_l3.png)
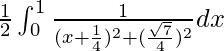
![Rendered by QuickLaTeX.com \left[\frac{1}{2}\frac{4}{\sqrt{7}}\tan^{-1}(\frac{x+\frac{1}{4}}{\frac{\sqrt{7}}{4}})\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c9d7b11410a5a98467c5427e0b0586d6_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{4}{2\sqrt{7}}\tan^{-1}(\frac{x+\frac{1}{4}}{\frac{\sqrt{7}}{4}})\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-084917ed9640ef8d40167fb7f2f1206c_l3.png)
![Rendered by QuickLaTeX.com \frac{4}{2\sqrt{7}}\left[\tan^{-1}(\frac{\frac{5}{4}}{\frac{\sqrt{7}}{4}})-\tan^{-1}(\frac{\frac{1}{4}}{\frac{\sqrt{7}}{4}})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e303c8083796eca125cb325dd8af4170_l3.png)