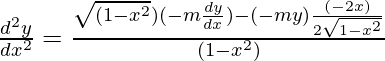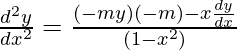Clase 12 Soluciones RD Sharma – Capítulo 22 Ecuaciones diferenciales – Ejercicio 22.3 | conjunto 2

Posted on by Rudeus Greyrat

Pregunta 11: Demuestra que y=(cx)/(1+cx) es la solución de la ecuación diferencial.

(1+x 2 )(dy/dx)+(1+y 2 )=0

Solución:

Tenemos,

 y=(cx)/(1+cx)                (yo)

Ecuación diferencial (i) con x,

\frac{dy}{dx}=\frac{(-1)(1+cx)-(c)(c-x)}{(1+cx)^2}

dy/dx=(-1-cx+cx-c 2 )/(1+cx) 2

dy/dx=-(c 2 +1)/(1+cx 2 ) 2

LHS,

(1+x 2 )(dy/dx)+(1+y 2 )

=(1+x2)[-(c2+1)/(1+cx2)2]+[1+(cx) 2 /(1+cx) 2 ]

=-\frac{(1+c^2)(1+x^2)}{(1+cx)^2}+[\frac{(1+cx)^2+(c-x)^2}{(1+cx)^2}]

Simplifica la ecuación anterior,

=0/(1+cx) 2

=0

Entonces, (1+x 2 )(dy/dx)+(1+y 2 )=0

Pregunta 12: Demuestra que y=e x (Acosx+Bsenx) es la solución de la ecuación diferencial.

d 2 y/dx 2 -2(dy/dx)+2y= 0

Solución:

tenemos,

y=e x (Acosx+Bsenx)              (i)

Ecuación diferencial (i) con x,

dy/dx=e x (Acosx+Bsenx)+e x (-Asenx+Bcosx)             (ii)

dy/dx=e x [(A+B)cosx-(AB)senx] (iii)

Nuevamente diferenciando la ecuación (ii) con x,

 d 2 y/dx 2 =e x (Acosx+Bsenx)+e x (-Asenx+Bcosx)+e x (-Asenx+Bcosx)+e x (-Acosx-Bsenx)

d 2 y/dx 2 =2e x [Bcosx-Asenx] (iv)

d2y/dx2=2e x [(A+B)cosx-(AB)senx] -2e x (Acosx+Bsenx)

d 2 y/dx 2 =2(dy/dx)-2y

d 2 y/dx 2 -2(dy/dx)+2y= 0

Pregunta 13: Verifica que y=cx+2c 2 es una solución de la ecuación diferencial.

2(dy/dx) 2 +x(dy/dx)-y=0

Solución:

tenemos,

y=cx+2c 2                (yo) 

Ecuación diferencial (i) con x,

dy/dx=c (ii)

LHS,

2(dy/dx) 2 +x(dy/dx)-y=2(c) 2 +x(c)-cx+2c 2

=0

Pregunta 14: Verifica que y=-x-1 es una solución de la ecuación diferencial. 

(yx)dy-(y 2 -x 2 )dx=0

Solución:

tenemos,

y=-x-1             (yo)

Ecuación diferencial (i) con x,

dy/dx=-1

LHS,

=(yx)dy-(y 2 -x 2 )dx

=(yx)(dy/dx)-(y 2 -x 2 )

=(-x-1-x)(-1)-[(-x-1) 2 -x 2 ]

=(2x+1)-(x2 + 2x +1- x2 )

=(x 2 -x 2 +2x-2x-1+1)

=0

Pregunta 15: Verifica que y 2 =4a(x+a) es una solución de la ecuación diferencial. 

y[1-(día/dx) 2 ]=2x(día/dx)

Solución:

tenemos,

y2 = 4a(x+a)            (i)

Ecuación diferencial (i) con x,

2y(dy/dx)=4a

(dy/dx)=(2a/y)

LHS,

=y[1-(dy/dx) 2 ]

=y[1-(2a/y) 2 ] 

=y[1-(4a 2 /y 2 )] 

=y[(y 2 -4a 2 )/y 2 ]

=(4a(x+a)-4a 2 )/y

=(4ax+4a 2 -4a 2 )/y  

=[2x(2a)]/y

=2x(dy/dx)

=lado derecho

Pregunta 16: Verifica que y=ce tan-1 x es una solución de la ecuación diferencial. 

(1+x 2 )(d 2 y/dx 2 )+(2x-1)(dy/dx)=0

Solución:

tenemos,

y=ce tan-1 x                 (i)

Ecuación diferencial (i) con x,

dy/dx=ce tan-1 x *(1/1+x 2 )   

(1+x2)(dy/dx)=y               (ii)

Nuevamente diferenciando la ecuación (ii) con x,

2x(dy/dx)+(1+x 2 )d 2 y/dx 2 =dy/dx

(2x-1)(dy/dx)+(1+x 2 )d 2 y/dx 2 =0

Pregunta 17: Verifica que y=e m cos-1 x es una solución de la ecuación diferencial. 

(1-x 2 )(d 2 y/dx 2 )-x(dy/dx)-m 2 y=0

Solución:

tenemos,

y=e m cos-1 x                 (i)

Ecuación diferencial (i) con x,

dy/dx=\frac{me^mcos^{-1}x}{-\sqrt{1-x^2}}

dy/dx = (ii)\frac{-my}{\sqrt{1-x^2}}                 

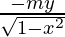
Nuevamente diferenciando la ecuación (ii) con x,

\frac{d^2y}{dx^2}=\frac{\sqrt{(1-x^2})(-m\frac{dy}{dx})-(-my)\frac{(-2x)}{2\sqrt{1-x^2}}}{(1-x^2)}

\frac{d^2y}{dx^2}=\frac{(-my)(-m)-x\frac{dy}{dx}}{(1-x^2)}

(1-x 2 )d 2 y/dx 2 =m 2 y-xdy/dx

(1-x 2 )d 2 y/dx 2 -m 2 y-xdy/dx=0

 Pregunta 18: Verifica que y=log(x+1/√(x 2 +a 2 )) 2 es una solución de la ecuación diferencial. 

(a 2 +x 2 )d 2 y/dx 2 +x(dy/dx)=0

Solución:

tenemos,

y=log(x+1/√(x 2 +a 2 )) 2               (i)

Ecuación diferencial (i) con x,

dy/dx=\frac{1}{(x+\sqrt{a^2+x^2})^2}*2(x+\sqrt{a^2+x^2})*\frac{d}{dx}(x+\sqrt{a^2+x^2}))

dy/dx =\frac{2}{(x+\sqrt{a^2+x^2})}*(1+\frac{2x}{2\sqrt{x^2+a^2}})

dy/dx=\frac{2}{(x+\sqrt{x^2+a^2})}\frac{(x+\sqrt{x^2+a^2})}{2\sqrt{x^2+a^2}}

\sqrt{x^2+a^2}(\frac{dy}{dx})=1                     (ii)

Nuevamente diferenciando la ecuación (ii) con x,

(√x 2 +a 2 ) d 2 y/dx 2 + (1/(2√x 2 +a 2 ))*(2x)*(dy/dx)=0

(a 2 +x 2 )d 2 y/dx 2 +x(dy/dx)=0

Pregunta 19: Muestre que la ecuación diferencial de la cual y=2(x 2 -1)+ce -x2 es la solución 

dy/dx+2xy=4x 3

Solución:

tenemos,

y=2(x 2 -1)+ce -x2                 (i)

Ecuación diferencial (i) con x,

dy/dx=4x+ce -x2 (-2x)

dy/dx=4x-2cxe- x2                     (ii)

LHS,

=dy/dx+2xy

= 4x-2cxe -x2 -2x(y=2(x 2 -1)+ce -x2   

= 4x-2cxe -x2 +4x 3 -4x+2xce -x2

=0

Pregunta 20: Demuestra que y=e -x +ax+c es la solución de la ecuación diferencial.

e x re 2 y/dx 2 =1

Solución:

Tenemos,

 y=e -x+ ax +c                       (i)

Ecuación diferencial (i) con x,

dy/dx=-e -x +a                 (ii)

Nuevamente diferenciando la ecuación (ii) con x,

d 2 y/dx 2 = e -1

(1/e -1 )d 2 y/dx 2 =1

e x re 2 y/dx 2 =1

Pregunta 21: Para cada una de las siguientes ecuaciones diferenciales verifique que la función que las acompaña sea una solución en el dominio mencionado.

(i) Función, y=ax , Ecuación diferencial, x(dy/dx)=y 

Solución:

Tenemos,

y=ax                     (yo)

Ecuación diferencial (i) con x,

dy/dx=a                  (ii)

De la ecuación (i) a=(y/x)

Poniendo el valor de a en la ecuación (i)

(dy/dx)=a

(dy/dx)=(y/x)

x(dy/dx)=y 

(ii) Función, y=±√(a 2 -x 2 ), Ecuación diferencial : x+y( dy/dx)=0 

Solución:

tenemos,

y=±√(a 2 -x 2 )                     (i)

Elevando al cuadrado ambos lados, tenemos

y 2 =(a 2 -x 2 )

2y(dy/dx)=-2x

x+y(dy/dx)=0 

(iii) Función, y=a/(x+a), Ecuación diferencial, y+x(dy/dx)=y 2 

Solución:

tenemos _

 y=a/(x+a)                 (yo)

Ecuación diferencial (i) con x,

dy/dx=a(-1)/(x+a) 2   

dy/dx=-a/(x+a) 2   

LHS,

 =y+x(dy/dx)

=a/(x+a)-ax/(x+a) 2 

=(-ax+ax+a 2 )/(x+a) 2

=a 2 /(x+a) 2

2 años

(iv) Función, y=ax+b+1/2x, Ecuación diferencial, x 3 d 2 y/dx 2 =1

Solución:

Tenemos,

y=ax+b+1/2x                 (yo)

Ecuación diferencial (i) con x,

dy/dx=a+1/(-2x 2 )

dy/dx=a-1/2x 2                              (ii)

Nuevamente diferenciando la ecuación (ii) con x,

d 2 y/dx 2 =0-(-2)/(2x 3 )

d 2 y/dx 2 = 1/x 3

x 3 d 2 y/dx 2 =1

(v) Función, y=(1/4)*(x±a) 2 , Ecuación diferencial, y=(dy/dx) 2 

Solución:

Tenemos,

y=(1/4)*(x±a) 2

Ecuación diferencial (i) con x,

dy/dx=(1/4)*2(x±a)

Elevando al cuadrado ambos lados, tenemos

(dy/dx) 2 =(1/4)*(x±a)2

(dy/dx) 2 =y

Publicación traducida automáticamente

Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *