Pregunta 11. Suponga que una gota de lluvia se evapora a una velocidad proporcional a su área de superficie. Forme una ecuación diferencial que involucre la tasa de cambio del radio de la gota de lluvia.
Solución:
Consideremos que ‘r’ es el radio de la gota de lluvia, el volumen de la gota es ‘V’ y el área de la gota es ‘A’
(dV/dt) proporcional a A
(dV/dt) – kA -(V disminuye con el aumento en t tan negativo cantar)
Aquí, k es constante de proporcionalidad,
= -k(4π r 2 )
4πr 2 (dr/dt) = -k(4πr 2 )
(dr/dt) = -k
Pregunta 12. Encuentra la ecuación diferencial de todas las parábolas con latus rectum 4a’ y cuyos ejes son paralelos al eje x.
Solución:
Ecuación de parábola cuya área es paralela al eje x y vértices en (h, k).
(y – k) 2 = 4a(x – h) -(1)
Al diferenciar wrt x,
2(y – k)(dy/dx) = 4a
(y – k)(dy/dx) = 2a
-(2)
De nuevo, diferenciando wrt x,
d 2 y/dx 2 (y – k) + (dy/dx)(dy/dx) = 0
2a(d 2 y/dx 2 ) + (dy/dx) 3 = 0
Pregunta 13. Demostrar que la ecuación diferencial de la cual 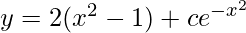 es solución, es (dy/dx) + 2xy = 4x 3
es solución, es (dy/dx) + 2xy = 4x 3
Solución:
-(1)
Al diferenciar wrt x,
Al sumar 2xy en RHS y LHS,
Al poner el valor de y en la ecuación anterior,
=
(dy/dx) + 2xy = 4x 3
Pregunta 14. De la ecuación diferencial que tiene y = (sen -1 x) 2 + A cos -1 x + B, donde A y B son constantes arbitrarias, como su solución general.
Solución:
y = (sen -1 x) 2 + A cos -1 x + B
Al diferenciar wrt x,
De nuevo, al diferenciar wrt x,
Pregunta 15. Formar la ecuación diferencial de la familia de curvas representada por la ecuación (siendo a el parámetro)
(i) (2x + a) 2 + y 2 = a 2
Solución:
(2x + a) 2 + y 2 = a 2 -(1)
Al diferenciar wrt x,
2(2x + a) + 2y(dy/dx) = 0
(2x + a) + y(dy/dx) = 0
a = -2x – y(dy/dx) -(2)
Al poner el valor de ‘a’ en la ecuación (1), tenemos
y2 = 4×2 + 4xy (dy/dx)
y 2 – 4x 2 – 4xy(dy/dx) = 0
(ii) (2x – a) 2 – y 2 = a 2
Solución:
(2x – a) 2 – y 2 = a 2
4x 2 – 4ax + un 2 – y 2 = un 2
4ax = 4x 2 – y 2
a = (4x 2 – y 2 )/4x
Al diferenciar wrt x,
4x 2 + y 2 = 2xy(dy/dx)
(iii) (x – a) 2 + 2y 2 = a 2
Solución:
(x – a) 2 + 2y 2 = a 2 -(1)
Al diferenciar wrt x,
2(x – a) + 4y(dy/dx) = 0
(x – a) + 2y(dy/dx) = 0
a = x + 2y(dy/dx) -(2)
Al poner el valor de a en la ecuación (1)
2y 2 – 4xy(dy/dx) – x 2 = 0
Pregunta 16. Representa las siguientes familias de curvas formando las ecuaciones diferenciales correspondientes (siendo a, b parámetros):
(i) x 2 + y 2 = un 2
Solución:
x 2 + y 2 = un 2
Al diferenciar wrt x,
2x + 2y(dy/dx) = 0
x + y(dy/dx) = 0
(ii) x 2 – y 2 = un 2
Solución:
x 2 – y 2 = un 2
Al diferenciar wrt x,
2x – 2y(dy/dx) = 0
x – y(dy/dx) = 0
(iii) y2 = 4ax
Solución:
y2 = 4ax
(y2/x) = 4a
Al diferenciar wrt x,
2xy(dy/dx) – y 2 = 0
2x(dy/dx) – y = 0
(iv) x 2 + (y – b) 2 = 1
Solución:
x 2 + (y – b) 2 = 1 -(1)
Al diferenciar wrt x,
2x + 2(y – b)(dy/dx) = 0
Al poner el valor de (y – b) en la ecuación (1)
x 2 (dy/dx) 2 + x 2 = (dy/dx) 2
x 2 [(dy/dx) 2 + 1] = (dy/dx) 2
(v) (x – a) 2 – y 2 = 1
Solución:
(x – a) 2 – y 2 = 1 -(1)
Al diferenciar wrt x,
2(x – a) – 2y(dy/dx) = 0
(x – a) – y(dy/dx) = 0
(x – a) = y(dy/dx)
Al poner el valor de (y – b) en la ecuación (i), obtenemos
y 2 (dy/dx) 2 – y 2 = 1
y 2 [(dy/dx)2 – 1] = 1
(vi)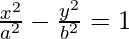
Solución:
Tenemos,
-(1)
{(bx) 2 – (ay) 2 } = (ab) 2 -(2)
Al diferenciar wrt x,
2xb 2 – 2a 2 y(dy/dx) = 0
xb 2 – a 2 y(dy/dx) = 0 -(3)
De nuevo, diferenciando wrt x,
Al poner el valor de b 2 en la ecuación (3), obtenemos
xb 2 – a 2 y(dy/dx) = 0
(vii) y 2 = 4a(x – b)
Solución:
Tenemos,
y 2 = 4a(x – b)
Al diferenciar wrt x,
2y(dy/dx) = 4a
Nuevamente diferenciando wrt x,
[(dy/dx) 2 + y(d 2 y/dx 2 )] = 0
(viii) y = eje 3
Solución:
Tenemos,
y = eje 3 -(1)
Al diferenciar wrt x,
(dy/dx) = 3ax 2
De la ecuación (1),
a=(y/x 3 -(1)
Al poner el valor de a en la ecuación (1)
dy/dx = 3(y/x 3 ) × x 2
x(dy/dx) = 3y
(ix) x 2 + y 2 = eje 3
Solución:
Tenemos,
x 2 + y 2 = eje 3
a = (x2 + y2 ) / ( x3 )
Al diferenciar wrt x,
2x 3 y(dy/dx) = x 4 + 3x 2 y 2
2x 3 y(dy/dx) = x 2 (x 2 + 3y 2 )
2xy (dy/dx) = (x2 + 3y2 )
(x) y = eje e
Solución:
Tenemos,
y = eje e -(1)
Al diferenciar wrt x,
dy/dx = ae hacha
dy/dx = ay -(2)
y = eje e
Al tomar registro de ambos lados, obtenemos
logía = hacha
a = (logía/x)
Ahora, pon el valor de ‘a’ en la ecuación (2)
(dy/dx) = lógica/x) × y
x(dy/dx) = ylogía
Pregunta 17. Forme la ecuación diferencial que representa la familia de elipses que tienen focos en el eje x y el centro en el origen.
Solución:
Tenemos,
Ecuación de elipse que tiene focos en el eje x,
-(donde a > b)
(bx) 2 + (ay) 2 = (ab) 2 -(1)
Al diferenciar la ecuación anterior wrt x,
2b 2x + 2a 2y (dy/dx) = 0
b 2 x + a 2 y(dy/dx) = 0 -(2)
De nuevo, diferenciando wrt x,
Al poner el valor de b 2 en la ecuación (2),
xb 2 + a 2 y(dy/dx) = 0
x[y(d 2 y/dx 2 ) + (dy/dx) 2 ] = y(dy/dx)
Pregunta 18. Forme la ecuación diferencial de la familia de hipérbolas que tienen focos en el eje X y centro en el origen
Solución:
Tenemos,
Ecuación de una hipérbola que tiene un centro en el origen y focos a lo largo del eje x
-(1)
(bx) 2 -(ay) 2 =(ab) 2 -(2)
Al diferenciar la ecuación anterior wrt x,
2xb 2 -2a 2 y(dy/dx)=0
xb 2 -a 2 y(dy/dx)=0 -(3)
De nuevo, diferenciando la ecuación anterior wrt x,
Poniendo el valor de b 2 en la ecuación (3),
xy(d 2 y/dx 2 ) + x(dy/dx) 2 – y(dy/dx) = 0
x[y(d 2 y/dx 2 ) +(dy/dx) 2 ] = y(dy/dx)
Esta es la ecuación diferencial requerida.
Pregunta 19. Formar la ecuación diferencial de la familia de círculos en el segundo cuadrante y tocando el eje de coordenadas.
Solución:
Tenemos,
Sean (-a, a) las coordenadas del centro de la circunferencia
Entonces, la ecuación del círculo está dada por,
(x + a) 2 + (y – b) 2 = a 2 -(1)
x2 + 2ax + a2 + y2 – 2ay + a2 = 0 -(2 )
Al diferenciar la ecuación anterior wrt x,
2x + 2a + 2y(dy/dx) – 2a(dy/dx) = 0
x + a + y(dy/dx) – a(dy/dx) = 0
Al sustituir el valor de ‘a’ en la ecuación (2)
Sea, (dy/dx) = p
[xp – x + x + yp] 2 + [yp – y – x – yp] 2 = [x + yp] 2
(x + y) 2 p 2 + (x + y) 2 = (x + yp) 2
(x + y) 2 [p 2 + 1] = (x + yp) 2 -(donde (dy/dx) = p)
Publicación traducida automáticamente
Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
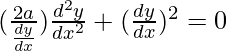
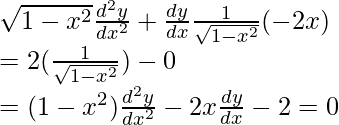
![Rendered by QuickLaTeX.com [\frac{4x(8x-2y\frac{dy}{dx}-4(4x^2-y^2}{(4x)^2}]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f2271fcae655de5d0e3678a7ee8a3617_l3.png)
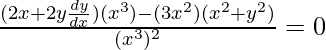
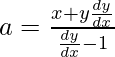
![Rendered by QuickLaTeX.com [x+\frac{x+y\frac{dy}{dx}}{\frac{dy}{dx}-1}]^2+[y-\frac{x+y\frac{dy}{dx}}{\frac{dy}{dx}-1}]^2=[\frac{x+y\frac{dy}{dx}}{\frac{dy}{dx}-1}]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d5cd8005a33cca3d1400ae42d9011cd_l3.png)