Derivadas de orden superior – Barcelona Geeks

La derivada de una función f(x) nos dice cómo cambiará el valor de la función cuando cambiemos x. Esta cantidad nos da una idea y la dirección sobre la tasa de cambio de la función. Por ejemplo, una derivada positiva indica el aumento en el valor de la función, mientras que un valor negativo indica que podría haber una disminución en el valor de la función. Los derivados son muy esenciales para nosotros en la predicción de los límites, la dirección del cambio y el comportamiento del sistema dada alguna entrada.

Derivadas y Derivadas de Orden Superior

La derivada de una función real nos dice acerca de la tasa de cambio de la función. Las derivadas se definen usando límites y para la función f(x), su derivada se denota por f'(x). Su definición en términos de límite se da a continuación,

$f'(x) = \lim _{h \to 0} \frac{f(x +h) - f(x)}{h}$

Para calcular derivadas de diferentes funciones, generalmente usamos las siguientes dos propiedades:

Regla de multiplicación para diferenciación

Digamos que tenemos una función complicada f(x) que es múltiplo de dos funciones más simples h(x) y g(x). En ese caso, usamos la fórmula de multiplicación para derivadas.

$\frac{d(g(x)h(x))}{dx} = g(x) \frac{d(h(x))}{dx} + h(x)\frac{g(f(x))}{dx}$

Regla de división para diferenciación

En otro caso, digamos que nuestra función complicada f(x) se compone de la división de dos funciones diferentes. Por ejemplo, f(x) = $\frac{g(x)}{h(x)}$

$\frac{d}{dx}(\frac{g(x)}{h(x)}) = \frac{g(x)h'(x) - h(x)g'(x)}{h(x)^2}$

Derivadas de segundo orden

Así como las derivadas nos dicen la tasa de cambio de las funciones, las derivadas de orden superior nos dicen la tasa de cambio de la derivada anterior. Por ejemplo, una derivada de segundo orden nos informa sobre la tasa de cambio de la derivada.

Digamos que tenemos una función f(x).

y = f(x)

$\frac{dy}{dx} = f'(x)$

Si f'(x) es derivable, podemos derivarla nuevamente para obtener una derivada de segundo orden. Se denota por,

$\frac{d(f'(x))}{dx} = \frac{d^2y}{dx^2}$

También se escribe como, f”(x).

Veamos algunos problemas con derivadas de segundo orden.

Problemas de muestra

Pregunta 1: Dado f(x) = x ³ . Encuentre el valor de f”(x).

Solución:

Primero tenemos que encontrar la derivada,

f(x) = ^x3

⇒f'(x) = 3x ²

Derivando de nuevo, obtenemos la derivada de segundo orden.

f”(x) = 6x

Pregunta 2: Dado f(x) = e ^x + sin(x). Encuentre el valor de f”(x).

Solución:

f(x) = e ^x + sin(x)

La primera derivada será,

f'(x) = e ^x + cos(x)

Diferenciándolo de nuevo,

f”(x) = e ^x – sen(x)

Pregunta 3: Dado f(x) = e ^x .sin(x). Encuentre el valor de f”(x) en x = 0.

Solución:

f(x) = e ^x .sin(x)

Como este es el producto de dos funciones, usaremos la propiedad de la multiplicación para las derivadas.

$\frac{d(f(x)g(x))}{dx} = f(x) \frac{d(g(x))}{dx} + g(x)\frac{d(f(x))}{dx}$

f'(x) = e ^x sen(x) + e ^x cos(x)

⇒ f'(x) = e ^x (sen(x) + cos(x))

f”(x) = e ^x (sen(x) + cos(x)) + e ^x (cos(x) -sen(x))

⇒f”(x) = e ^x (2cos(x))

⇒f”(x) = 2e ^x cos(x)

en x = 0.

f”(0) = 2

Pregunta 4: Dado f(x) = e ^x .sin(x). Encuentre el valor de f”(x) en x = 0.

Solución:

f(x) = e ^x .sin(x)

Como este es el producto de dos funciones, usaremos la propiedad de la multiplicación para las derivadas.

$\frac{d(f(x)g(x))}{dx} = f(x) \frac{d(g(x))}{dx} + g(x)\frac{d(f(x))}{dx}$

f'(x) = e ^x sen(x) + e ^x cos(x)

⇒ f'(x) = e ^x (sen(x) + cos(x))

f”(x) = e ^x (sen(x) + cos(x)) + e ^x (cos(x) -sen(x))

⇒f”(x) = e ^x (2cos(x))

⇒f”(x) = 2e ^x cos(x)

Pregunta 5: Dado y = 3e ^2x + 2e ^3x , prueba que $\frac{d^2y}{dx^2} -5\frac{dy}{dx} + 6y =0$

Solución:

y = 3e ^2x + 2e ^3x

y’ = 6e ^2x + 6e ^3x

y” = 12e ^2x + 18e ^3x

Sustituyendo estos valores en la ecuación,

$\frac{d^2y}{dx^2} -5\frac{dy}{dx} + 6y =0$

⇒12e ^2x + 18e ^3x – 5(6e ^2x + 6e ^3x ) + 6(3e ^2x + 2e ^3x )= 0

⇒12e ^2x + 18e ^3x – 30e ^2x – 30e ^3x + 18e ^2x + 12e ^3x = 0

⇒-30e ^2x + 30e ^3x – 30e ^2x – 30e ^3x = 0

⇒ 0 = 0

Por lo tanto, Probado.

Pregunta 6: Dado y = e ^x (x + 1). Encuentra el valor de la segunda derivada en x = 1.

Solución:

y = e ^x (x + 1)

Como esta función es producto de dos funciones, usaremos la regla de la multiplicación para la derivada.

$\frac{d(f(x)g(x))}{dx} = f(x) \frac{d(g(x))}{dx} + g(x)\frac{d(f(x))}{dx}$

y’ = e ^x (x + 1) + e ^x

Ahora podemos diferenciarlo nuevamente para obtener la segunda derivada.

y”= $\frac{d(e^x(x+1))}{dx} + \frac{d(e^x)}{dx}$

Nuevamente, esta función requerirá la regla de la multiplicación para la diferenciación.

y” = e ^x (x + 1) + e ^x + e ^x

⇒ y” = e ^x (x + 3)

Pregunta 7: Dado y = $\frac{x}{x^2 + 1}$ . Encuentra el valor de la segunda derivada en x = 1.

Solución:

y = $\frac{x}{x^2 + 1}$

Como esta función es la división de dos funciones, usaremos la regla de división para la derivada.

$\frac{d}{dx}(\frac{g(x)}{h(x)}) = \frac{g(x)h'(x) - h(x)g'(x)}{h(x)^2}$

y’ = $\frac{(x^2+1) - x(2x)}{(x^2 + 1)^2}$

⇒ y’ = $\frac{1 - x^2}{(x^2 + 1)^2}$

Ahora podemos diferenciarlo nuevamente para obtener la segunda derivada.

Nuevamente, esta función requerirá la regla de la multiplicación para la diferenciación.

y”= $\frac{(x^2 + 1)^2(-2x) - (1 - 2x^2)(2(x^2+1)2x)}{(x^2 + 1)^4}$

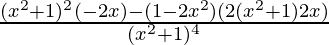
En x = 1,

y” = $\frac{(1^2 + 1)^2(-2) - (1 - 21^2)(2(1^2+1)2)}{(1^2 + 1)^4}$

⇒ y” = $\frac{(2)^2(-2) - (1 - 2)(2(2)2)}{(2)^4}$

⇒ y” = $\frac{-8 + 8}{(2)^4}$

⇒ y” = 0