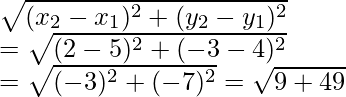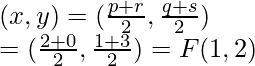Clase 10 Soluciones RD Sharma – Capítulo 14 Geometría de coordenadas – Ejercicio 14.5 | Serie 1

Posted on by Rudeus Greyrat

 Pregunta 1. Encuentra el área de un triángulo cuyos vértices son:

(i) (6, 3), (-3, 5) y (4, -2)

Solución:

Supongamos que ABC es un triángulo cuyos vértices son A(6, 3), B(-3, 5) y C(4, -2)

Asi que, 

Área de ∆ABC = 1/2[x 1 (y 2 – y 3 ) + (y 3 – y 1 )x 2 + x 3 (y 1 – y 2 )]

= 1/2[6(5 + 2) + (-3)(-2 – 3) + 4(3 – 5)]

= 1/2[6(5 + 2) + (-3)(-2 – 3) + 4(3 – 5)]

= 1/2[42 + 15 – 8]

= 1/2 * 49

= 49/2 unidad cuadrada

(ii) (en 1 2 , 2 en 1 ), (en 2 2 , 2 en 2 ) y (en 3 2 , 2 en 3 ) 

Solución:

Supongamos que ABC es un triángulo cuyos vértices son A(en 1 2 , 2en 1 ), (en 2 2 , 2en 2 ) y (en 3 2 , 2en 3 ) 

Área de ∆ABC = 1/2[x 1 (y 2 – y 3 ) + (y 3 – y 1 )x 2 + x 3 (y 1 – y 2 )]

= 1/2[en 1 2 ( 2 en 2 – 2 en 3 ) + en 2 2 ( 2 en 3 – 2 en 1 ) + en 3 2 ( 2 en 1 – 2 en 2 )]

= 1/2[en 1 2 2en 2 – en 1 2 2en 3 + en 2 2 2en 3 – en 2 2 2en 1 + en 3 2 2en 1 – en 3 2 2en 2 ]

= 1/2 × 2a 2 [t 1 2 t 2 – t 1 2 t 3 + t 2 2 t 3 – t 2 2 t 1 + t 3 2 t 1 – t 3 2 t 2 ]

= un 2 [t 1 2 (t 2 – t 3 )+ t 2 2 (t 3 – t 1 )+ t 3 2 (t 1 – t 2 )]

(iii) (a, c + a), (a, c) y (-a, c – a)

Supongamos que ABC es un triángulo cuyos vértices son A(a, c + a), B(a, c) y C(-a, c – a)

Entonces, Área de ∆ABC = 1/2[x 1 (y 2 – y 3 ) + (y 3 – y 1 )x 2 + x 3 (y 1 – y 2 )]

= 1/2[a(c – c + a)a(c – a – c – a) + (-a)(c + a – c)]

= 1/2(a 2 – 2a 2 – a 2 )

= 1/2(-2a 2 )

= a 2 unidades cuadradas

Pregunta 2. Encuentra el área de los cuadriláteros, las coordenadas de cuyos vértices son

(i) (-3, 2), (5, 4), (7, -6) y (-5, -4)

Solución:

Consideremos que ABCD es un cuadrilátero cuyos vértices son A(-3, 2), B(5, 4), C(7, -6) y D(-5, -4)

Entonces, Área de ABCD = Área de ∆ABC+ Área de ∆ADC ….(1)

Asi que, 

Entonces, Área de ∆ABC = 1/2[x 1 (y 2 – y 3 ) + (y 3 – y 1 )x 2 + x 3 (y 1 – y 2 )]

= 1/2 [-3(4 + 6) + (-6 – 2) + 7(2 – 4)]

= 1/2 [-3(10) + 5 * (-8) + 7 * (-2)]

= 1/2 [-30 – 40 – 14]

= 1/2 [-30-40-14]

= 1/2 (-84)

= -42 

= 42 unidades cuadradas (El área no puede estar en negativo)

De manera similar, el área de ∆ADC

= 1/2 [-3(-6 + 4) + 7(-4 – 2) + (-5)(2 + 6)]

 = 1/2 [-3(-2) + 7(-6) + (-5)(8)]

 = 1/2 [6 – 42 – 40]

= 1/2 (-76) 

= -38

= 38 unidades cuadradas (el área no puede estar en negativo)

Ahora ponga todos estos valores en la ecuación (1), obtenemos

Área del cuadrilátero ABCD = 42 + 38 = 80 unidades cuadradas

(ii) (1, 2), (6, 2), (5, 3) y (3, 4)

Solución:

Consideremos que ABCD es un cuadrilátero cuyos vértices son A(1, 2), B(6, 2), C(5, 3) y D(3, 4)

Entonces, Área de ABCD = Área de ∆ABC+ Área de ∆ADC ….(1)

Entonces, Área de ∆ABC = 1/2[x 1 (y 2 – y 3 ) + (y 3 – y 1 )x 2 + x 3 (y 1 – y 2 )]

= 1/2 [1(2 – 3) + 6(3 – 2) + 5(2 – 2)]

= 1/2[-1 + 6 + 0]

= 1/2 (5) 

= 5/2 unidades cuadradas

De manera similar, el área de ∆ADC

= 1/2 [1(3 – 4) + 5(4 – 2) + 3(2 – 3)] 

= 1/2 [1 * (-1) + 5 * 2 + 3 * (-1)] 

= 1/2 [-1 + 10 – 3]

= 1/2 * 6 

= 3 unidades cuadradas

Ahora ponga todos estos valores en la ecuación (1), obtenemos

Área del cuadrilátero ABCD = 5/2 + 3 = (5 + 6)/2 = 11/2 unidades cuadradas 

(iii) (-4, -2), (-3, -5), (3, -2), (2, 3) 

Solución:

Consideremos que ABCD es un cuadrilátero cuyos vértices son A(-4, -2), B(-3, -5), C(3, -2), D(2, 3) 

Entonces, Área de ABCD = Área de ∆ABC+ Área de ∆ADC ….(1)

Entonces, Área de ∆ABC = 1/2[x 1 (y 2 – y 3 ) + (y 3 – y 1 )x 2 + x 3 (y 1 – y 2 )]

= 1/2 [-4(-5 + 2) – 3(-2 + 2) + 3(-2 + 5)]

 = 1/2 [-4 * (-3) – 3 * 0 + 3 * 3]

 = 1/2 [12 + 0 + 9] 

= 1/2 * 21 

= 21/2 unidades cuadradas

Del mismo modo, el área de ∆ADC,

= 1/2 [-4(-2 – 3) + 3(3 + 2) + 2(-2 + 2)] 

= 1/2[-4 * (-5) + 3 * 5 + 2 * 0]

= 1/2 [20 + 15 + 0] 

= 1/2 * 35

= 35/2 unidades cuadradas

Ahora ponga todos estos valores en la ecuación (1), obtenemos

Área del cuadrilátero ABCD = 21/2 + 35/2 + 56/2 = 28 unidades cuadradas

Pregunta 3. Los cuatro vértices de un cuadrilátero son (1, 2), (-5, 6), (7, -4) y (k, -2) tomados en orden. Si el área del cuadrilátero es cero, encuentra el valor de k?

Solución:

Consideremos que ABCD es un cuadrilátero cuyos vértices son A(1, 2), B(-5, 6), C(7, -4) y D(k, -2)

Entonces, Área de ABCD = Área de ∆ABC+ Área de ∆ADC ….(1)

Ahora área de ∆ABC

= 1/2[x 1 (y 2 – y 3 ) + (y 3 – y 1 )x 2 + x 3 (y 1 – y 2 )]

= 1/2 [1(6 + 4) + (-5)(-4 – 2) + 7(2 – 6)]

= 1/2 [1 * 10 + (-5)(-6) + 7(-4)]

= 1/2 [10 + 30 – 28]

= 1/2 × 12 

= 6 unidades cuadradas

Del mismo modo, el área de ∆ADC,

= 1/2 [1(-4 + 2) + 7(-2 – 2) + k(2 + 4)]

= 1/2 [1(-2) + 7(-4) + k(-4)]

 = 1/2 [-2 – 28 + 6k]

= 1/2 (-30 + 6k) 

= -15+3k

= 3k – 15 unidades cuadradas

Ahora ponga todos estos valores en la ecuación (1), obtenemos

Área del cuadrilátero ABCD = 6 + 3k – 15

Pero se da que el área del cuadrilátero ABCD = 0  

Asi que, 

0 = 6 + 3k – 15

k = 9/3 = 3

Por lo tanto, el valor de k es 3.

Pregunta 4. Los vértices de ∆ABC son (-2, 1), (5, 4) y (2, -3) respectivamente. Encuentre el área del triángulo y la longitud de la altura a través de A.

Solución:

Dado que ABC es un triángulo cuyos vértices son A(-2, 1), B(5, 4) y C(2, -3)

y AD ⊥ BC, supongamos AD = h

Entonces, área de ∆ABC = 1/2[x 1 (y 2 – y 3 ) + (y 3 – y 1 )x 2 + x 3 (y 1 – y 2 )]

= 1/2 [-2(4 + 3) + 5(-3 – 1) + 2(1 – 4)]

= 1/2 [-2 * 7 + 5 * (-4) + 2(-3)]

= 1/2[-14 – 20 – 6] 

= 1/2 * (-40)

= -20

= 20 unidades cuadradas

Ahora encontramos la longitud de BC = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(2-5)^2+(-3-4)^2}\\ =\sqrt{(-3)^2+(-7)^2}=\sqrt{9+49}

= √58 unidades

Entonces, el área de ∆ABC = 1/2 * base * altura

⇒ 20 = 1/2 * 58 * hora 

⇒ h = (20 * 2)/√58 = 40/√58 unidades

Pregunta 5. Demuestre que los siguientes conjuntos de puntos son colineales

(i) (2, 5), (4, 6) y (8, 8)

Solución:

Como sabemos que 3 puntos son colineales el area del triangulo formado por ellos es cero

Entonces, supongamos que ABC es un triángulo cuyos vértices A(2, 5), B(4, 6) y C(8, 8)

Entonces, área de ∆ABC = 1/2[x 1 (y 2 – y 3 ) + (y 3 – y 1 )x 2 + x 3 (y 1 – y 2 )]

= 1/2[2(6 – 8 + 4(8 – 5) + 8(5 – 6)]

= 1/2 [2 * (-2) + 4 * 3 + 8 * (-1)]

= 1/2 [-4 + 12 – 8]

= 1/2 * 0 = 0

Área de ∆ABC = 0

Por lo tanto, los puntos A, B y C son colineales                                 

Por lo tanto probado

(b) (1, -1), (2, 1) y (4, 5)

Solución:

Como sabemos que 3 puntos son colineales el area del triangulo formado por ellos es cero

Entonces, supongamos que ABC es un triángulo cuyos vértices A(1, -1), B(2, 1) y C(4, 5)

Entonces, área de ∆ABC = 1/2[x 1 (y 2 – y 3 ) + (y 3 – y 1 )x 2 + x 3 (y 1 – y 2 )]

= 1/2 [1(1 – 5) + 2(5 + 1) + 4(-1 – 1)]

= 1/2 [1(-4) + 2 * 6 + 4(-2)]

= 1/2 [-4 + 12 – 8]

= 1/2 * 0 = 0

Área de ∆ABC = 0

Por lo tanto, los puntos A, B y C son colineales                                 

Por lo tanto probado

Pregunta 6. Encuentra el área de un cuadrilátero ABCD, las coordenadas de cuyos vértices son A (-3, 2), B (5, 4), C (7, -6) y D (-5, -4). 

Solución:

Dado eso, ABCD es un cuadrilátero cuyos vértices son A (-3, 2), B (5, 4), C (7, -6) y D (-5, -4). 

Entonces, Área del cuadrilátero ABCD = área de ∆ABC+ área de ∆ACD

= 1/2|(-12 – 30 + 14) – (10 + 28 + 18)| + 1/2|(18 – 28 – 10) – (14 + 30 + 12)|

= 1/2|-28 – 56| + 1/2|-20 – 56|

= 1/2|-84| + 1/2|-76|

= 42 + 38

= 80 unidades cuadradas

Por lo tanto, el área del cuadrilátero es de 80 unidades cuadradas.

Pregunta 7. En ∆ABC, las coordenadas del vértice A son (0, -1) y D (1, 0) y E (0, 1) respectivamente, los puntos medios de los lados AB y AC. Si F es el punto medio del lado C, encuentra el área de ∆DEF. 

Solución:

Dado que ∆ABC, las coordenadas del vértice A son (0, -1) y D (1, 0) y E (0, 1) son

los puntos medios de los lados AB y AC

Consideremos B (p, q), C (r, s) y F (x, y)

Entonces, Punto medio de AB = Coordenadas de D

(\frac{0+p}{2},\frac{-1+q}{2})=(1,0)

p/2 = 1

p = 2

Por lo tanto, B(p, q) = B(2, 1)

(-1 + q)/2 = 0

-1 + q = 0

q = 1

Punto medio de AC = coordenadas de E

(\frac{0+r}{2},\frac{-1+s}{2})=(0,1)

r/2 = 0

r = 0

(-1 + s)/2 = 1

-1 + s = 2

s = 3

Ahora, C(r, s) = C(0, 3)

Coordenadas de F = Punto medio de BC

(x,y)=(\frac{p+r}{2},\frac{q+s}{2})\\ =(\frac{2+0}{2},\frac{1+3}{2})=F(1,2)

Entonces, las coordenadas de A(0,-1), B(2, 1) y C(0, 3)

Área de ∆ABC = 1/2[x 1 (y 2 – y 3 ) + (y 3 – y 1 )x 2 + x 3 (y 1 – y 2 )]

= 1/2 [0(1 – 3) + 2(3 + 1) + 0(-1 – 1)]

= 1/2(8) = 4 unidades cuadradas

Y la coordenada de D(1, 0), E(0, 1) y F(1, 2)

Área de ∆DEF = 1/2[1(1 – 2) + 0(2 – 0) + 1(0 – 1)]

= 1/2(-1 – 1) = -1

= 1 unidad cuadrada (El área no puede estar en negativo)

Pregunta 8. Encuentra el área del triángulo PQR con Q (3, 2) y los puntos medios de los lados que pasan por Q siendo (2, -1) y (1, 2). 

Solución:

Dado que, ∆PQR, L y N son puntos medios de QR y QP, y las coordenadas de Q son (3, 2) de L son (2, -1) y de N son (1, 2)

Supongamos que las coordenadas de R sean (x 1 , y 1 ) y P(x 2 ,y 2 )

2 = (3 + x 1 )/2 ⇒ 3 + x 1 = 4 ⇒ x 1 = 4 – 3 = 1

y -1 = (2 + y)/2 ⇒ -2 = 2 + y ⇒ y = -2 – 2 = -4 

Las coordenadas de R son (1,-4)

Del mismo modo, las coordenadas de P serán 

1 = (3 + x 1 )/2 ⇒ 3 + x 1 = 2 ⇒ x 1 = 2 – 3 = -1

y (2 + y)/1 = 2 ⇒ 2 + y = 4 ⇒ y = 4 – 2 = 2

Las coordenadas de P son (-1, 2)

Ahora área de ∆PQR

= 1/2 [(-12 + 2 – 2) – (2 + 4 + 6)]

= 1/2[-12 – 12] = -12

= 12 unidades cuadradas

Pregunta 9. Si P (-5, -3), Q (-4, -6), R (2, -3) y S (1, 2) son los vértices de un cuadrilátero PQRS, halla su área.

Solución:

Dado que, el cuadrilátero PQRS cuyos vértices son P (-5, -3), Q (-4, -6), R (2, -3) y S (1, 2) 

Área del cuadrilátero PQRS = Área de ∆PQR + Área de ∆PSR ….(1)

Ahora área de ∆PQR = 1/2[x 1 (y 2 – y 3 ) + (y 3 – y 1 )x 2 + x 3 (y 1 – y 2 )]

= 1/2[-5(-6 + 3) + (-4)(-3 + 3) + 2(-3 + 6)]

= 1/2[-5 * (-3) + (-4 * 0) + 2 * 3]

= 1/2(15 + 0 + 6)

= 1/2 * 21 

= 21/2

Análogamente, el área ∆PSR,

= 1/2[-5 * (2 + 3) + 1(-3 + 3) + 2(-3 – 2)]

= 1/2[-5 * 5 + 1 * 0 + 2 * (-5)]

= 1/2[-25 + 0 – 10]

= 1/2 * (-35)

= -35/2

Ahora ponga todos estos valores en la ecuación (1), obtenemos

Área del cuadrilátero PQRS = 21/2 + (-35/2) = 28 unidades cuadradas

Pregunta 10. Si A (-3, 5), B (-2, -7), C (1, -8) y D (6, 3) son los vértices de un cuadrilátero ABCD, encuentra su área. 

Solución:

Consideremos que ABCD es un cuadrilátero cuyos vértices son A (-3, 5), B (-2, -7), C (1, -8) y D (6, 3)

Entonces, Área de ABCD = Área de ∆ABC+ Área de ∆ACD ….(1)

Entonces, Área de ∆ABC = 1/2[x 1 (y 2 – y 3 ) + (y 3 – y 1 )x 2 + x 3 (y 1 – y 2 )]

= 1/2 [-3(-7 + 8) + (-2)(-8 – 5) + 1(5 + 7)]

= 1/2 [-3 * 1 + 26 + 12]

= 1/2[-3 + 26 + 12]

= 35/2 unidades cuadradas

De manera similar, el área de ∆ACD = 1/2[-3(-8 – 3) + 1(3 – 5) + 6(5 + 8)] 

= 1/2 [-3 * (-11) + 1(-2) + 6 * 13] 

= 1/2[33 – 2 + 78]

= 1/2 * 109

= 109/2 unidades cuadradas

Ahora ponga todos estos valores en la ecuación (1), obtenemos

Área del cuadrilátero ABCD = 35/2 + 109/2 = 144/2 = 72 unidades cuadradas

Pregunta 11. ¿Para qué valor de ‘a’ los puntos (a, 1), (1, -1) y (11, 4) son colineales?

Solución:

Supongamos que los vértices de ∆ABC son A (a, 1), B (1, -1) y C (11, 4)

Ahora área de ∆ABC = 1/2[x 1 (y 2 – y 3 ) + (y 3 – y 1 )x 2 + x 3 (y 1 – y 2 )]

= 1/2[a(-1 – 4) + 1(4 – 1) + 11(1 + 1)]

= 1/2[-5a + 3 + 22]

= 1/2(25 – 5a)

Se da que los puntos A,B y C son colineales 

entonces, área de ∆ABC = 0

1/2 (25 – 5a) = 0  

⇒ 25 – 5a = 0

⇒ a = 25/5 = 5

Por lo tanto, el valor de a es 5

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *