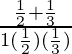Clase 10 Soluciones RD Sharma – Capítulo 5 Razones trigonométricas – Ejercicio 5.2

Pregunta 27. Si A = B = 60°, verifica que

(i) cos(A − B) = cos A cos B + sen A sen B

Solución:

Sabemos sen 60° = √3/2, sen 30° = 1/2

Poniendo los valores de A y B en la siguiente ecuación

cos(60° − 60°) = cos60°cos60° + sen60°sen60°

cos(0) = cos ² 60° + sen ² 60°

1 = (1/2) ² + (√3/2) ²

1 = 1/4 + 3/4

1 = 4/4 = 1

Por lo tanto probado

(ii) sen(A − B) = sen A cos B − cos A sen B

Solución:

Poniendo los valores de A y B en la siguiente ecuación

sen(60° − 60°) = sen60°cos60° − cos60°sen60°

sen(0°) = (1/2)(√3/2) – (√3/2)(1/2)

0 = √3/4 – √3/4

0 = 0

Por lo tanto probado

(iii) tan(A − B) = 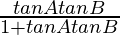$\frac{tanA−tanB}{1+tanAtanB}$

Solución:

Poniendo los valores de A y B en la siguiente ecuación

tan(60° − 60°) = $\frac{tan60°−tan60°}{1+tan60°tan60°}$

tan0 = $\frac{0}{1+tan60°tan60°}$

0 = 0

Por lo tanto probado

Pregunta 28. Si A = 30° y B = 60°, verifica que

(i) sen(A + B) = sen A cos B cos A sen B

Solución:

Sabemos sen 60° = cos 30° = √3/2, sen 30° = cos 60° = 1/2

Poniendo los valores de A y B en las siguientes ecuaciones

sen(30° + 60°) = sen 30° cos 60° cos 30° sen 60°

sen 90° = (1/2)(1/2) + (√3/2)(√3/2)

1 = 1/4 + 3/4

1 = 1

Por lo tanto probado

(ii) cos(A + B) = cos A cos B − sen A sen B

Solución:

Poniendo los valores de A y B en las siguientes ecuaciones

cos(30° + 60°) = cos 30° cos 60° – sen 30° sen 60°

cos 90° = (√3/2)(1/2) – (1/2)(√3/2)

0 = √3/4 – √3/4

0 = 0

Por lo tanto probado

Pregunta 29. Si sen(A + B) = 1 y cos(A − B) = 1, 0° < A + B ≤ 90° y A ≥ B, encuentra A y B.

Solución:

Dado sen(A + B) = 1, cos(A − B) = 1, 0° < A + B ≤ 90° y A ≥ B,

Sabemos que, sen90° = 1 y cos0° = 1

sin(A + B) = 1 y sin90∘= 1

Podemos decir eso

(A + B) = 90° -(1)

cos(A − B) = 1 y cos0° = 1

(A − B) = 0°

A = B-(2)

Sustituyendo la ecuación (2) en (1)

A + A = 90°

2A = 90°

A = 45°

A = B = 45°

Pregunta 30. Si tan(A + B) = √3 y tan(A − B) = 1/√3, 0° < A + B ≤ 90°; A > B, encuentre A y B.

Solución:

Dado tan(A + B) = √3

tan(A − B) = 1/√3

0∘< A + B ≤ 90∘y A > B,

Sabemos que, tan30° = 1/√3 y tan60° = √3

Ahora,

tan(A + B) = √3 y tan60 = √3

(A + B) = 60° -(1)

Otra vez,

tan(A − B) = 1/√3 y tan30° = 1/√3

(A − B) = 30° -(2)

Resolviendo las ecuaciones (1) y (2),

(A + B) = 60°

(A-B) = 30°

Resolviendo las dos ecuaciones anteriores obtenemos

2A = 90°

A = 90°/2 = 45°

Pregunta 31. Si sen(A – B) = 1/2 y cos(A + B) = 1/2, 0° < A + B ≤ 90°; A < B, encuentre A y B.

Solución:

Dado, sen(A − B) = 1/2

cos(A + B) = 1/2

0° < A + B ≤ 90° y A < B,

Sabemos que, sen30° = 1/2 y cos60° = 1/2

Como sen(A − B) = 1/2 y sen30° = 1/2

Entonces (A − B) = 30° -(1)

Otra vez

cos(A + B) = 1/2 y cos60° = 1/2

Entonces (A + B) = 60° -(2)

Resolviendo las ecuaciones (1) y (2) obtenemos

2A = 90°

A = 90°/2 = 45°

de (2)

(A + B) = 60°

Además, A = 45°

B = 60° – 45°

B = 15°

Por lo tanto, A = 45°, B = 15°

Pregunta 32. En un ∆ABC en ángulo recto en B, ∠A = ∠C. Encuentre los valores de

(i) sen A cos C+ cos A sen C

Solución:

Dado: En ∆ABC en ángulo recto en B, ∠A = ∠C

Sabemos en un triángulo ∠A + ∠B +∠C = 180°

2∠A = 180° – 90° = 45° [∠B = 90°]

Ahora,

Tenemos sen A cos C+ cos A sen C

Poner los valores de cada ángulo

sen 45° cos 45° + cos 45° sen 45°

= (1/√2)(1/√2) + (1/√2)(1/√2)

= 1/2 + 1/2

= 1

(ii) sen A sen B + cos A cos B

Solución:

Tenemos sen A sen B + cos A cos B

Poner los valores de cada ángulo

sen 45° sen 90° + cos 45° cos 90°

= (1/√2)(1) + (1/√2)(0)

= (1/√2) + 0

= 1/√2

Pregunta 33. Halla los ángulos agudos A y B, si sen(A + 2B) = √3/2 y cos(A + 4B) = 0, y A > B.

Solución:

Dado, sin(A + 2B) = √3/2, cos(A + 4B) = 0, A > B,

Sabemos que sen60° = √3/2 y cos90° = 0

Como sen(A + 2B) = √3/2 y sen60° = √3/2

Entonces (A + 2B) = 60° -(1)

De nuevo cos(A + 4B) = 0 y cos90° = 0

Entonces (A + 4B) = 90° -(2)

De (1) de (2) obtenemos,

2B = 30°

B = 30°/2 = 15°

de (2)

(A + 4B) = 90°

Además, B = 15°

A = 90° − 60°

A = 30°

Por lo tanto, A = 30°, B = 15°

Pregunta 34. En ΔPQR, rectángulo en Q, PQ = 3 cm y PR = 6 cm. Determina ∠P y ∠R.

Solución:

Dado en ΔPQR, rectángulo en Q, PQ = 3 cm y PR = 6 cm.

Sabemos cos P = Base/Hipotenusa =3/6

cos 60° = 1/2

Entonces ∠P = 60°

En ΔPQR

∠P + ∠Q + ∠R = 180°

∠R = 180° – 90° – 60°

∠R = 30°

Por lo tanto, ∠P = 60°, ∠R = 30°

Pregunta 35. Si sen(A − B) = sen A cos B − cos A sen B y cos(A − B) = cos A cos B + sen A sen B, encuentre los valores de sen15° y cos15°.

Solución:

Para encontrar sen15°:

Tenemos sin15° = sin(45° – 30°)

A = 45° y B = 30°

Ahora poniendo los valores de A y B en la siguiente ecuación

sen(A − B) = sen A cos B − cos A sen B

sen(45° − 30°) = sen 45° cos 30° − cos 45° sen 30°

sin15° = (1/√2)(√3/2) – (1/√2)(1/2))

sin15° = (√3 – 1)/2√2

Para encontrar cos15°:

cos15° = cos(45° – 30°)

A = 45° y B = 30°

Nuevamente poniendo los valores de A y B en la siguiente ecuación

cos(A − B) = cos A cos B + sen A sen B

cos(45° − 30°) = cos 45° cos 30° + sen 45° sen 30°

sin15° = (1/√2)(√3/2) + (1/√2)(1/2))

sin15° = (√3 + 1)/2√2

Pregunta 36. En un △ABC recto, rectángulo en C, si ∠B = 60° y AB = 15 unidades. Encuentra los ángulos y lados restantes.

Solución:

Dado En un △ABC recto en ángulo recto en C, ∠B = 60° ∠C = 90°

Sabemos en un triángulo ∠A + ∠B + ∠C = 180°

∠A = 180° – 150° = 30°

sen 30° = BC/AB = BC/15

BC/15 = 1/2

BC = 7,5 unidades

cos 30° = AC/AB = AC/15

CA/15 = √3/2

CA = 15√3/2 unidades

Pregunta 37. Si ΔABC es un triángulo rectángulo tal que ∠C = 90°, ∠A = 45° y BC = 7 unidades. Encuentra ∠B, AB y AC.

Solución:

Dado: En ΔABC ∠C = 90°, ∠A = 45° y BC = 7 unidades

Sabemos en un triángulo ∠A + ∠B + ∠C = 180°

∠B = 180° – 135° = 45°

porque B = BC/AB = 7/AB

cos 45° = 7/AB

7/AB = 1/√2

AB = 7/√2 unidades

bronceado A = BC/AC

tan 45° = 7/AC

7/CA = 1

CA = 7 unidades

Pregunta 38. En un rectángulo ABCD, AB = 20 cm, ∠BAC = 60°, calcula el lado BC y las diagonales AC, BD.

Solución:

Dado: rectángulo ABCD, AB = 20 cm, ∠BAC = 60°

tan 60° = BC/AC

√3 = BC/20

BC = 20√3 cm

cos 60° = AB/AC

1/2 = 20/CA

CA = 40 cm

en un rectangulo ambas diagonales son iguales

Pregunta 39. Si A y B son ángulos agudos tales que tan A = 1/2, tan B = 1/3 y tan(A + B) = 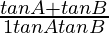$\frac{tanA+tanB}{1−tanAtanB}$ hallar (A + B).

Solución:

Dado, A y B son ángulos agudos tales que tanA = 1/2 y tanB = 1/3

tan(A + B) = $\frac{tanA+tanB}{1−tanAtanB}$

tan(A + B) = $\frac{\frac{1}{2}+\frac{1}{3}}{1−(\frac{1}{2})(\frac{1}{3})}$

tan(A + B) = $\frac{\frac{5}{6}}{1−\frac{1}{6}}$

tan(A + B) = $\frac{\frac{5}{6}}{\frac{5}{6}}$

tan(A + B) = 1

Lo sabemos, tan45° = 1

Por lo tanto, (A + B) = 45°

Pregunta 40. Demuestra que (√3 + 1)(3 – cot 30°) = tan ³ 60° – 2sin 60°

Solución:

Tomando RHS

tan ³ 60° – 2sen 60°

(√3) – 2(√3/2) = 3√3 – √3 = 2√3

Ahora tomando LHS

(√3 + 1)(3 – cuna 30°)

= (√3 + 1)(3 – √3)

= (√3 + 1)√3(√3 – 1)

= 2√3

LHS = RHS

Por lo tanto probado

Publicación traducida automáticamente

Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 10 Soluciones RD Sharma – Capítulo 5 Razones trigonométricas – Ejercicio 5.2 | conjunto 3

Pregunta 27. Si A = B = 60°, verifica que

(i) cos(A − B) = cos A cos B + sen A sen B

(ii) sen(A − B) = sen A cos B − cos A sen B

(iii) tan(A − B) = $\frac{tanA−tanB}{1+tanAtanB}$

Pregunta 28. Si A = 30° y B = 60°, verifica que

(i) sen(A + B) = sen A cos B cos A sen B

(ii) cos(A + B) = cos A cos B − sen A sen B

Pregunta 29. Si sen(A + B) = 1 y cos(A − B) = 1, 0° < A + B ≤ 90° y A ≥ B, encuentra A y B.

Pregunta 30. Si tan(A + B) = √3 y tan(A − B) = 1/√3, 0° < A + B ≤ 90°; A > B, encuentre A y B.

Pregunta 31. Si sen(A – B) = 1/2 y cos(A + B) = 1/2, 0° < A + B ≤ 90°; A < B, encuentre A y B.

Pregunta 32. En un ∆ABC en ángulo recto en B, ∠A = ∠C. Encuentre los valores de

(i) sen A cos C+ cos A sen C

Pregunta 33. Halla los ángulos agudos A y B, si sen(A + 2B) = √3/2 y cos(A + 4B) = 0, y A > B.

Pregunta 34. En ΔPQR, rectángulo en Q, PQ = 3 cm y PR = 6 cm. Determina ∠P y ∠R.

Pregunta 35. Si sen(A − B) = sen A cos B − cos A sen B y cos(A − B) = cos A cos B + sen A sen B, encuentre los valores de sen15° y cos15°.

Pregunta 36. En un △ABC recto, rectángulo en C, si ∠B = 60° y AB = 15 unidades. Encuentra los ángulos y lados restantes.

Pregunta 37. Si ΔABC es un triángulo rectángulo tal que ∠C = 90°, ∠A = 45° y BC = 7 unidades. Encuentra ∠B, AB y AC.

Pregunta 38. En un rectángulo ABCD, AB = 20 cm, ∠BAC = 60°, calcula el lado BC y las diagonales AC, BD.

Pregunta 39. Si A y B son ángulos agudos tales que tan A = 1/2, tan B = 1/3 y tan(A + B) = $\frac{tanA+tanB}{1−tanAtanB}$ hallar (A + B).

Pregunta 40. Demuestra que (√3 + 1)(3 – cot 30°) = tan ³ 60° – 2sin 60°

Deja una respuesta Cancelar la respuesta

Pregunta 27. Si A = B = 60°, verifica que

(i) cos(A − B) = cos A cos B + sen A sen B

(ii) sen(A − B) = sen A cos B − cos A sen B

(iii) tan(A − B) =

Pregunta 28. Si A = 30° y B = 60°, verifica que

(i) sen(A + B) = sen A cos B cos A sen B

(ii) cos(A + B) = cos A cos B − sen A sen B

Pregunta 29. Si sen(A + B) = 1 y cos(A − B) = 1, 0° < A + B ≤ 90° y A ≥ B, encuentra A y B.

Pregunta 30. Si tan(A + B) = √3 y tan(A − B) = 1/√3, 0° < A + B ≤ 90°; A > B, encuentre A y B.

Pregunta 31. Si sen(A – B) = 1/2 y cos(A + B) = 1/2, 0° < A + B ≤ 90°; A < B, encuentre A y B.

Pregunta 32. En un ∆ABC en ángulo recto en B, ∠A = ∠C. Encuentre los valores de

(i) sen A cos C+ cos A sen C

Pregunta 33. Halla los ángulos agudos A y B, si sen(A + 2B) = √3/2 y cos(A + 4B) = 0, y A > B.

Pregunta 34. En ΔPQR, rectángulo en Q, PQ = 3 cm y PR = 6 cm. Determina ∠P y ∠R.

Pregunta 35. Si sen(A − B) = sen A cos B − cos A sen B y cos(A − B) = cos A cos B + sen A sen B, encuentre los valores de sen15° y cos15°.

Pregunta 36. En un △ABC recto, rectángulo en C, si ∠B = 60° y AB = 15 unidades. Encuentra los ángulos y lados restantes.

Pregunta 37. Si ΔABC es un triángulo rectángulo tal que ∠C = 90°, ∠A = 45° y BC = 7 unidades. Encuentra ∠B, AB y AC.

Pregunta 38. En un rectángulo ABCD, AB = 20 cm, ∠BAC = 60°, calcula el lado BC y las diagonales AC, BD.

Pregunta 39. Si A y B son ángulos agudos tales que tan A = 1/2, tan B = 1/3 y tan(A + B) = hallar (A + B).

Pregunta 40. Demuestra que (√3 + 1)(3 – cot 30°) = tan 3 60° – 2sin 60°

Deja una respuesta Cancelar la respuesta

(iii) tan(A − B) = $\frac{tanA−tanB}{1+tanAtanB}$

Pregunta 39. Si A y B son ángulos agudos tales que tan A = 1/2, tan B = 1/3 y tan(A + B) = $\frac{tanA+tanB}{1−tanAtanB}$ hallar (A + B).

Pregunta 40. Demuestra que (√3 + 1)(3 – cot 30°) = tan ³ 60° – 2sin 60°