Pregunta 1. Encuentra 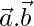 cuándo
cuándo
(yo) 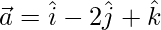 y
y 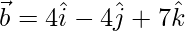
Solución:
=
= (1)(4) + (-2)(-4) + (1)(7)
= 4 + 8 + 7
= 19
(ii) ![]() y
y ![]()
Solución:
=
= (0)(2) + (1)(0) + (2)(1)
= 2
(iii) ![]() y
y ![]()
Solución:
=
= (0)(2) + (1)(3) + (-1)(-2)
= 0 + 3 + 2
= 5
Pregunta 2. ¿Para qué valor de λ son el vector 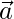 y
y 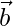 perpendiculares entre sí? dónde:
perpendiculares entre sí? dónde:
(yo) 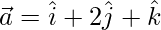 y
y 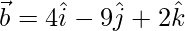
Solución:
y
son perpendiculares entre si
Asi que
⇒
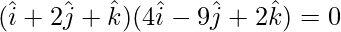
⇒ λ(4) + (2)(-9) + (1)(2) = 0
⇒ 4λ – 18 + 2 = 0
⇒ 4λ = 16
⇒ λ = 4
(ii) 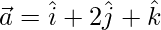 y
y 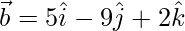
Solución:
y
son perpendiculares entre si
entonces
= 0
⇒
⇒ λ(5) + (2)(-9) + (1)(2) = 0
⇒ 5λ – 18 + 2 = 0
⇒ 5λ = 16
⇒ λ = 16/5
(iii) 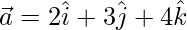 y
y 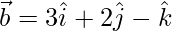
Solución:
y
son perpendiculares entre si
entonces
= 0
⇒
=0
⇒ (2)(3) + (3)(2) – (4)λ = 0
⇒ 6 + 6 – 4λ = 0
⇒ 4λ = 12
⇒ λ = 3
(iv) 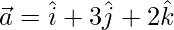 y
y 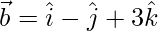
Solución:
y
son perpendiculares entre si
asi que
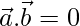
⇒
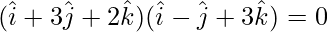
⇒ λ(1) + (3)(-1) + (2)(3) = 0
⇒ λ – 3 + 6 = 0
⇒ λ = 3
Pregunta 3. Si 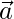 y
y 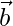 son dos vectores tales que |
son dos vectores tales que | 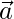 |=4, |
|=4, | 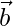 | = 3 y
| = 3 y 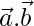 = 6. Encuentra el ángulo entre
= 6. Encuentra el ángulo entre 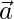 y
y 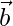
Solución:
Sea el ángulo θ
cos θ =
= 6 /(4×3) = 1/2
Por lo tanto, θ = cos -1 (1/2)
= π/3
Pregunta 4. Si 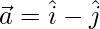 y
y 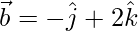 , encuentra
, encuentra 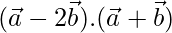 .
.
Solución:
=
=
=
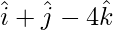
=
=
=
Ahora,
=
= (1)(1) + (1)(-2) + (-4)(2)
= 1 – 2 – 8
= -9
Por lo tanto,
= -9
Pregunta 5. Encuentra el ángulo entre los vectores 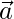 y
y 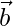 donde:
donde:
(yo) 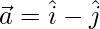 y
y 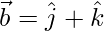
Solución:
Sea el ángulo θ entre
y
cos θ =
Ahora,
=
= (1)(0) + (-1)(1) + (0)(1)
= 0 – 1 + 0 = -1
|
|= |
|
=
= √2
= |
|
=
= √2
Ahora, cos θ = -1/(√2×√2)
= -1/2
θ = cos -1 (-1/2)
= 2π/3
(ii) 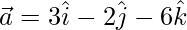 y
y 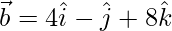
Solución:
Sea el ángulo θ entre
y
Ahora,
=
=(3)(4) + (-2)(-1) + (-6)(8)
= 12 + 2 – 48
= -34
|
| = |
|
=
= √49 = 7
=
= √81 = 9
cos θ =
Ahora, cos θ = -34/(7×9)
= -34/63
θ = cos -1 (-34/63)
(iii) 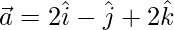 y
y 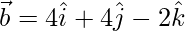
Solución:
Sea el ángulo θ entre
y
Ahora,
=
= (2)(4) + (-1)(4) + (2)(-2)
= 8 – 4 – 4 = 0
|
| = |
|
=
= √9 = 3
|
| = |
|
=
= √36 = 6
Ahora, cos θ =
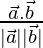
cos θ = 0/(3×6) = 0
θ = cos -1 (0)
θ = π/2
(iv) 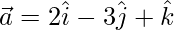 y
y 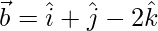
Solución:
Sea el ángulo θ entre
y
Ahora,
=
= (2)(1) + (-3)(1) + (1)(-2)
= 2 – 3 – 2
= -3
|
| =
=
= √14
|
| =|
|
=
= √6
cos θ =
Ahora, cos θ = -3/(√14×√6)
= -3/√84
θ = cos -1 (-3/√84)
(v) 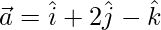 y
y 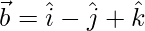
Solución:
Sea el ángulo θ entre
y
Ahora,
=
= (1)(1) + (2)(-1) + (-1)(1)
= 1 – 2 – 1
= -2
|
| = |
|
=
= √6
|
| = |
|
=
= √3
cos θ =
Ahora, cos θ = -2/(√6×√3)
= -2/√18
= -2/3√2
θ = cos -1 (-√2 /3)
Pregunta 6. Encuentra los ángulos que forman los vectores 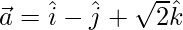 con los ejes de coordenadas.
con los ejes de coordenadas.
Solución:
Los componentes a lo largo de los ejes x, y y z son
y
respectivamente.
Sea el ángulo entre
y
θ 1
Ahora,
=
= (1)(1) + (-1)(0) + (√2)(0)
= 1
=
= √4 = 2
= √1 = 1
cos θ 1 =
Ahora, cos θ 1 = 1/(2×1)
= 1/2
θ 1 = cos -1 (1/2) = π/3
Sea el ángulo entre
y
θ 2
Ahora,
=
= (1)(0) + (-1)(1) + (√2)(0)
= -1
= √1 = 1
cos θ 2 =
Ahora, cos θ 2 = -1/(2×1)
= -1/2
θ 2 = cos -1 (-1/2) = 2π/3
Sea el ángulo entre
y
θ 3
Ahora,
=
= (1)(0) + (-1)(0) + (√2)(1)
= √2
= √1 = 1
cos θ 3 =
= 1/(√2)
= cos -1 (1/√2) = π/4
Pregunta 7(i). Producto escalar de un vector con 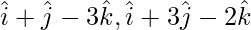 y
y 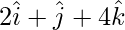 son 0, 5 y 8 respectivamente. Encuentra el vector.
son 0, 5 y 8 respectivamente. Encuentra el vector.
Solución:
Sean
y
tres vectores dados.
Sea
un vector tal que sus productos escalares con
, y
sean 0, 5 y 8 respectivamente. Después,
⇒
= 0
⇒ x + y – 3z = 0 ….(1)
⇒
= 5
⇒ x + 3y – 2z = 5 …..(2)
⇒
= 8
⇒ 2x + y + 4z = 8 …..(3)
Resolviendo 1,2 y 3 obtenemos x = 1, y = 2 y z = 1,
Por lo tanto, el vector requerido es
Pregunta 8. Si 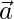 y
y 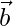 son vectores unitarios inclinados en un ángulo θ, entonces demuestre que
son vectores unitarios inclinados en un ángulo θ, entonces demuestre que
(i) cos θ/2 = 1/2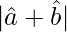
Solución:
|
| = |
| = 1
|
| 2 =(
) 2
=
= 1 + 1 + 2
= 2 + 2|
|cos θ
= 2(1 + (1)(1)cos θ)
= 2(2 cos 2 θ/2)
|
| 2 = 4 cos 2 θ/2
= 2 cos θ/2
cos θ/2 = 1/2|
|
(ii) tan θ/2 = 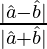
Solución:
= 1
=
=
=
=
=
= tan 2 θ/2
Por lo tanto, tan θ/2 =
Pregunta 9. Si la suma de dos vectores unitarios es un vector unitario, prueba que la magnitud de su diferencia es √3.
Solución:
Sean
y
dos vectores unitarios
Después,
Según pregunta:
Tomando cuadrados en ambos lados
⇒
⇒
⇒ (1) 2 +(1) 2 +
= 1
⇒ 2+ 2
= 1
⇒ 2
= -1
⇒ \sombrero{a}.\sombrero{b} =-1/2
Ahora,
=
= (1) 2 + (1) 2 – 2 (-1/2)
= 2 + 1 = 3
Por lo tanto,
= 3
=√3
Pregunta 10. Si 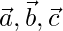 son tres vectores unitarios perpendiculares entre sí, entonces demuestre que |
son tres vectores unitarios perpendiculares entre sí, entonces demuestre que | 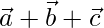 | =√3.
| =√3.
Solución:
Dados
son mutuamente perpendiculares por lo que,
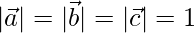
Ahora,
=
=
= (1) 2 + (1) 2 + (1) 2 + 0
= 3
= √3
Pregunta 11. Si 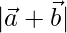 = 60,
= 60, 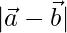 = 40 y
= 40 y 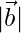 = 46, encuentra
= 46, encuentra 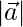
Solución:
Dado
= 60,
= 40 y
= 46
Lo sabemos,
(a + b) 2 + (a – b) 2 = 2(a 2 + b 2 )
⇒
⇒ 60 2 + 40 2 = 2 (
2 + 49 2 )
⇒ 3600 + 1600 = 2
+ 2401
⇒
= 968
⇒
= √484 =22
Pregunta 12. Demuestre que el vector 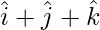 está igualmente inclinado con los ejes de coordenadas.
está igualmente inclinado con los ejes de coordenadas.
Solución:
Dejar
√(1+1+1) = √3
Sean θ 1 , θ 2 , θ 3 el ángulo entre los ejes coordenados y el
cos θ 1 =
= 1/√3
cos θ 2 =
= 1/√3
cos θ 3 =
= 1/√3
Ya que, cos θ 1 = cos θ 2 = cos θ 3
Por lo tanto, el vector dado tiene la misma inclinación que el eje de coordenadas.
Pregunta 13. Muestre que los vectores 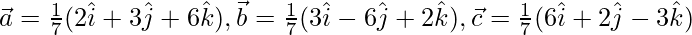 son vectores unitarios mutuamente perpendiculares.
son vectores unitarios mutuamente perpendiculares.
Solución:
Dado,
= (1/7)√(2 2 + 3 2 + 6 2 ) = (1/7)(√49) = 1
= (1/7)√(3 2 + (-6) 2 + 2 2 ) = (1/7)(√49) = 1
= (1/7)√(6 2 + 2 2 + (-3) 2 ) = (1/7)(√49) = 1
Ahora,
1/49[3 × 2 – 3 × 6 + 6 × 2]
= 1/49[6 – 18 + 12] = 0
1/49[3 × 6 – 6 × 2 – 2 × 3]
= 1/49[18 – 12 – 6] = 0
Ya que
son vectores unitarios mutuamente perpendiculares.
Pregunta 14. Para cualesquiera dos vectores 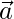 y
y 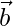 , Demuestre que
, Demuestre que 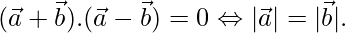
Solución:
Probar
⇒
⇒
⇒
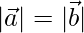
Por lo tanto probado
Pregunta 15. Si 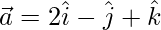 ,
, 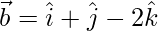 y
y 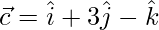 , encuentran tal que
, encuentran tal que 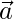 es perpendicular a
es perpendicular a 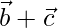 .
.
Solución:
Dado:
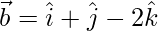
segun pregunta
⇒
⇒
⇒ 2(λ+1) – (λ+3) -2λ-1 = 0
⇒ 2λ + 2 -λ – 3 – 2λ – 1 = 0
⇒ -λ = 2
⇒ λ = -2
Pregunta 16. Si 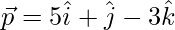 y
y 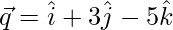 , entonces encuentra el valor de λ tal que
, entonces encuentra el valor de λ tal que 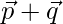 y
y 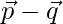 sean vectores perpendiculares.
sean vectores perpendiculares.
Solución:
Dado,
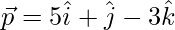
segun pregunta
⇒
⇒
⇒
⇒ 25 + λ 2 + 9 = 1 + 9 + 25
⇒ λ 2 = 1
⇒ λ = 1
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA