Encuentre el valor exacto de sen 330°

La trigonometría es la relación entre los ángulos y los lados de un triángulo rectángulo. En un triángulo rectángulo, hay 3 ángulos de los cuales un ángulo es un ángulo recto (90°) y otros dos ángulos son ángulos agudos y hay 3 lados. El lado opuesto al ángulo recto se llama hipotenusa. Hay 6 razones entre estos lados basadas en el ángulo entre ellos y se llaman razones trigonométricas.

Las 6 razones trigonométricas son:

Seno (pecado)
Coseno (cos)
Tangente (bronceado)
Cosecante (cosec)
secante (seg)
Cotangente (cuna)

Todas las funciones trigonométricas son positivas en el 1er cuadrante. Solo sen y cosec son positivos en el segundo cuadrante. Solo tan y cot son positivos en el 3er cuadrante y solo cos y sec son positivos en el 4to cuadrante.

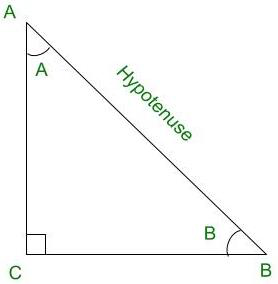
Triángulo rectángulo ACB

Seno (pecado):

El seno de un ángulo se define por la relación entre las longitudes de los lados opuestos al ángulo y la hipotenusa. Para el triángulo anterior, el valor del ángulo seno se da tanto para ∠A como para ∠B, la definición de ángulo del seno es la relación entre la perpendicular y su hipotenusa.

$Sin A = \frac{P}{H}= \frac{CB}{AB}$

$SinB = \frac{P}{H}= \frac{AC}{AB}$

Coseno (cos):

El coseno de un ángulo se define por la relación entre las longitudes de los lados adyacentes al ángulo y la hipotenusa. Para el triángulo anterior, el valor del ángulo cos se da tanto para ∠A como para ∠B, la definición del ángulo cos es la relación entre la base y su hipotenusa.

$CosA = \frac{B}{H}= \frac{AC}{AB}$

$CosB = \frac{B}{H}= \frac{CB}{AB}$

Tangente (bronceado):

La tangente de un ángulo se define por el cociente entre la longitud de los lados opuestos al ángulo y la longitud del lado adyacente al ángulo. Para el triángulo anterior, el valor del ángulo tan se da tanto para ∠A como para ∠B, la definición de ángulo tan es la relación entre la perpendicular y su base.

$TanA = \frac{P}{B}= \frac{CB}{AC}$

$TanB = \frac{P}{B}= \frac{AC}{CB}$

Cosecante (cosec):

La cosecante de un ángulo se define por el cociente entre la longitud de la hipotenusa y el lado opuesto al ángulo. Para el triángulo anterior, el valor del ángulo cosec se da tanto para ∠A como para ∠B, la definición de ángulo cosec es la relación entre la hipotenusa y su perpendicular.

$CosecA = \frac{H}{P}= \frac{AB}{CB}$

$CosecB = \frac{H}{P}= \frac{AB}{AC}$

Secante (s):

La secante de un ángulo se define por la relación entre la longitud de la hipotenusa y el lado y el lado adyacente al ángulo. Para el triángulo anterior, el valor del ángulo sec se da tanto para ∠A como para ∠B, la definición de ángulo sec es la relación entre la hipotenusa y su base.

$SecA = \frac{H}{P}= \frac{AB}{AC}$

$SecB = \frac{H}{P}= \frac{AB}{CB}$

Cotangente (cot):

La cotangente de un ángulo se define por la relación entre la longitud de los lados adyacentes al ángulo y el lado opuesto al ángulo. Para el triángulo anterior, el valor del ángulo cot se da tanto para ∠A como para ∠B, la definición de ángulo cot es la relación entre la hipotenusa y su base.

$CotA = \frac{B}{P}= \frac{AC}{CB}$

$CotB = \frac{B}{P}= \frac{CB}{AC}$

Encuentre el valor exacto de sen (330°)

Solución:

el pecado es negativo en el cuarto cuadrante

$\therefore$ sen (360° – θ) = – sen θ

330° se encuentra en el cuarto cuadrante.

$\therefore$ pecado (330°) = pecado (360° – 30°)

$\therefore$ pecado (330°) = – pecado (30°)

$\therefore$ pecado (330°) = – $\frac{1}{2}$ ……. (Ya que, sen(30°) = $\frac{1}{2}$ )

$\therefore$ pecado (330°) = – 0,5

Por lo tanto, el valor exacto de sen (330°) es – $\frac{1}{2}$ .

Problemas similares

Pregunta 1: Encuentra el valor exacto de cosec (270°)

Solución:

cosec es positivo solo en el 1er y 2do Cuadrante.

270° no se encuentra en el 1er y 2do Cuadrante.

$\therefore$ cosec (360° – θ) = – cosec θ

$\therefore$ coseg (270°) = coseg (360° – 90°)

$\therefore$ coseg (270°) = – coseg (90°)

$\therefore$ coseg (270°) = – 1 ……. (Ya que, cosec(90°) = 1)

Por lo tanto, el valor exacto de cosec (270°) es – 1 .

Pregunta 2: Encuentra el valor de cos (150°)

Solución:

cos es negativo en el segundo cuadrante

$\therefore$ coseno (180° – θ) = – coseno θ

150° se encuentra en el segundo cuadrante.

$\therefore$ coseno (150°) = coseno (180° – 30°)

$\therefore$ coseno (150°) = – coseno (30°)

$\therefore$ cos (150°) = – $\frac{√3}{2}$ ……. (Ya que, cos(30°) = $\frac{√3}{2}$ )

Por lo tanto, el valor exacto de cos (150°) es – $\frac{√3}{2}$ .

Pregunta 3: Encuentra el valor de tan (225°)

Solución:

tan es positivo en el 3er cuadrante

$\therefore$ bronceado (180° + θ) = bronceado θ

225° se encuentra en el 3er Cuadrante.

$\therefore$ bronceado (225°) = bronceado (180° + 45°)

$\therefore$ bronceado (225°) = bronceado (45°)

$\therefore$ bronceado (225°) = 1 ……. (Ya que, tan(45°) = 1)

Por lo tanto, el valor de tan (225°) es 1.

Pregunta 4: Encuentra el valor de cosec (225°)

Solución:

cosec es negativo en el 3er Cuadrante.

$\therefore$ cosec (180° + θ) = – cosec θ

225° se encuentra en el 3er Cuadrante.

$\therefore$ coseg (225°) = coseg (180° + 45°)

$\therefore$ coseg (225°) = – coseg (45°)

$\therefore$ cosec (225°) = – √2 ……. (Ya que, cosec(45°) = √2)

Por lo tanto, el valor de cosec (225°) es √2.

Pregunta 5: Encuentra el valor de cot (315°)

Solución:

cot es negativo en el cuarto cuadrante

$\therefore$ cuna (360° – θ) = – cuna θ

315° se encuentra en el 3er Cuadrante.

$\therefore$ cuna (315°) = – cuna (360° – 45°)

$\therefore$ cuna (315°) = – cuna (45°)

$\therefore$ cuna (315°) = – 1 ……. (Ya que, cuna(45°) = 1)

Por lo tanto, el valor de cot (315°) es -1.

Publicación traducida automáticamente

Artículo escrito por rajsanghavi9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Encuentre el valor exacto de sen (330°)

Problemas similares

Deja una respuesta Cancelar la respuesta