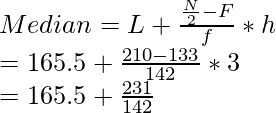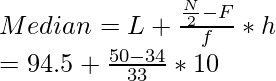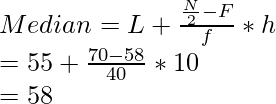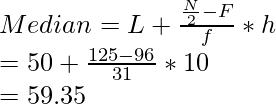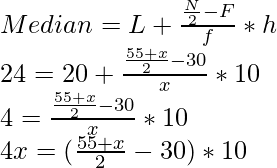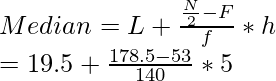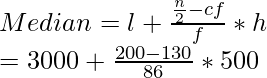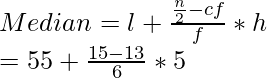Pregunta 1. Las siguientes son las vidas en horas de 15 piezas de los componentes del motor de un avión. Encuentre la mediana:
715, 724, 725, 710, 729, 745, 694, 699, 696, 712, 734, 728, 716, 705, 719.
Solución:
Al ordenar las observaciones en orden ascendente, tenemos
694, 696, 699, 705, 710, 712, 715, 716, 719, 721, 725, 728, 729, 734, 745
El número de términos en la secuencia de observación es impar, es decir, N = 15
Ahora,
Mediana = (N + 1)/ 2º término
= (15 + 1)/2 o término
= 8vo término
Por lo tanto, 716, que es el octavo término , es la mediana de los datos.
Pregunta 2. La siguiente es la distribución de altura de los estudiantes de cierta clase en cierta ciudad:
| Altura (en cm): | 160 – 162 | 163 – 165 | 166 – 168 | 169 – 171 | 172 – 174 |
| No de estudiantes: | 15 | 118 | 142 | 127 | 18 |
Encuentre la altura mediana.
Solución:
Intervalo de clase (exclusivo) Intervalo de clase (inclusive) Frecuencia de intervalo de clase Frecuencia acumulada 160 – 162 159,5 – 162,5 15 15 163 – 165 162,5 – 165,5 118 133 (F) 166 – 168 165,5 – 168,5 142(f) 275 169 – 171 168,5 – 171,5 127 402 172 – 174 171,5 – 174,5 18 420 norte = 420 Tenemos N = 420,
Entonces, N/2 = 420/ 2 = 210
Ahora, la frecuencia acumulada apenas mayor que N/2 es 275
Por lo tanto, 165,5 – 168,5 es la clase mediana st
L = 165,5, f = 142, F = 133 y h = (168,5 – 165,5) = 3
= 165,5 + 1,63
= 167,13
Pregunta 3. A continuación se muestra la distribución del coeficiente intelectual de 100 estudiantes. Encuentre el coeficiente intelectual medio
| CI: | 55 – 64 | 65 – 74 | 75 – 84 | 85 – 94 | 95 – 104 | 105 – 114 | 115 – 124 | 125 – 134 | 135 – 144 |
| No de estudiantes: | 1 | 2 | 9 | 22 | 33 | 22 | 8 | 2 | 1 |
Solución:
Intervalo de clase (exclusivo) Intervalo de clase (inclusive) Frecuencia de intervalo de clase Frecuencia acumulada 55 – 64 54,5 – 64,5 1 1 65 – 74 64,5 – 74,5 2 3 75 – 84 74,5 – 84,5 9 12 85 – 94 84,5 – 94,5 22 34 (F) 95 – 104 94,5 – 104,5 33(f) 67 105 – 114 104,5 – 114,5 22 89 115 – 124 114,5 – 124,5 8 97 125 – 134 124,5 – 134,5 2 98 135 – 144 134,5 – 144,5 1 100 norte = 100 norte = 100,
Por lo tanto, N/2 = 100/ 2 = 50
La frecuencia acumulada apenas mayor que N/ 2 es 67, entonces la clase mediana es (94.5 – 104.5) st,
L = 94,5, F = 33, h = (104,5 – 94,5) = 10
= 94,5 + 4,85
= 99,35
Pregunta 4. Calcula la mediana a partir de los siguientes datos:
| Renta (en Rs): | 15 – 25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 | 75-85 | 85-95 |
| No de casas: | 8 | 10 | 15 | 25 | 40 | 20 | 15 | 7 |
Solución:
Intervalo de clases Frecuencia Frecuencia acumulada 15 – 25 8 8 25 – 35 10 18 35 – 45 15 33 45 – 55 25 58 (F) 55 – 65 40(f) 98 65 – 75 20 118 75 – 85 15 133 85 – 95 7 140 norte = 140 norte = 140,
Y, N/2 = 140/ 2 = 70
La frecuencia acumulada apenas mayor que N/ 2 es 98, entonces la clase media es 55 – 65 st,
L = 55, f = 40, F = 58, h = 65 – 55 = 10
Pregunta 5. Calcula la mediana a partir de los siguientes datos:
| Marcas a continuación: | 0-10 | 10 – 20 | 20 – 30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| No de estudiantes: | 15 | 35 | 60 | 84 | 96 | 127 | 198 | 250 |
Solución:
Marcas debajo Nº de alumnos Intervalo de clases Frecuencia Frecuencia acumulada 10 15 0-10 15 15 20 35 10-20 20 35 30 60 20-30 25 60 40 84 30-40 24 84 50 96 40-50 12 96(F) 60 127 50-60 31(f) 127 70 198 60-70 71 198 80 250 70-80 52 250 norte = 250 norte = 250,
Y, N/2 = 250/ 2 = 125
La frecuencia acumulada un poco mayor que N/ 2 es 127, entonces la clase media es 50 – 60 st,
L = 50, f = 31, F = 96, h = 60 -50 = 10
Pregunta 6. Calcular la frecuencia faltante de la siguiente distribución, dado que la mediana de la distribución es 24.
| Edad en años: | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| Nº de personas: | 5 | 25 | ? | 18 | 7 |
Solución:
Supongamos que la frecuencia desconocida es x.
Intervalo de clases Frecuencia Frecuencia acumulada 0 – 10 5 5 10-20 25 30 (F) 20-30 x(f) 30 + x 30-40 18 48 + x 40-50 7 55 + x N=170 Dado: Mediana = 24
Por lo tanto,
Clase mediana = 20 – 30; L = 20, h = 30 -20 = 10, f = x, F = 30
4x = 275 + 5x – 300
4x – 5x = – 25
– x = – 25
X = 25
Por lo tanto, x = 25
Pregunta 7. La siguiente tabla muestra la distribución de frecuencia de mujeres casadas por edad al matrimonio.
| Edad en años) | Frecuencia | Edad en años) | Frecuencia |
| 15 – 19 | 53 | 40 – 44 | 9 |
| 20 – 24 | 140 | 45 – 49 | 5 |
| 25 – 29 | 98 | 45 – 49 | 3 |
| 30 – 34 | 32 | 55 – 59 | 3 |
| 35 – 39 | 12 | 60 y más | 2 |
Calcular la mediana e interpretar los resultados.
Solución:
Intervalo de clase (exclusivo) Intervalo de clase (inclusive) Frecuencia Frecuencia acumulada 15 – 19 14,5 – 19,5 53 53 (F) 20 – 24 19,5 – 24,5 140(f) 193 25 – 29 24,5 – 29,5 98 291 30 – 34 29,5 – 34,5 32 323 35 – 39 34,5 – 39,5 12 335 40 – 44 39,5 – 44,5 9 344 45 – 49 44,5 – 49,5 5 349 50 – 54 49,5 – 54,5 3 352 55 – 54 54,5 – 59,5 3 355 60 y más 59.5 y superior 2 357 norte = 357 norte = 357,
Y, N/2 = 357/ 2 = 178,5
La frecuencia acumulada apenas mayor que N/2 es 193,
Por lo tanto, la clase mediana es 19.5 – 24.5 st
l = 19,5, f = 140, F = 53, h = 25,5 – 19,5 = 5
Mediana = 23,98, eso implica que casi la mitad de las mujeres están casadas entre los 15 y los 25 años.
Pregunta 8. La siguiente tabla muestra la distribución del tiempo de vida de 400 lámparas de neón:
| Tiempo de vida: (en horas) | Número de lámparas |
| 1500 – 2000 | 14 |
| 2000 – 2500 | 56 |
| 2500 – 3000 | 60 |
| 3000 – 3500 | 86 |
| 3500 – 4000 | 74 |
| 4000 – 4500 | 62 |
| 4500 – 5000 | 48 |
Encuentre la vida media.
Solución:
Toda la vida Número de lámparas fi Frecuencia acumulada (cf) 1500 – 2000 14 14 2000 – 2500 56 70 2500 – 3000 60 130 (F) 3000 – 3500 86 216 3500 – 4000 74 290 4000 – 4500 62 352 4500 – 5000 48 400 norte = 400 Ahora
norte = 400
Y la frecuencia acumulada apenas mayor que n/2 (= 200) es 216, que pertenece al intervalo de clase 3000 – 3500
Clase mediana = 3000 – 3500. Por lo tanto,
(l) = 3000 y, (f) de la clase mediana = 86, (cf) de la clase anterior a la clase mediana = 130 y (h) = 500
Tenemos,
= 3000 + (35000/86)
= 3406,98 horas, que es el tiempo medio de las lámparas.
Pregunta 9. La siguiente distribución da el peso de 30 estudiantes en una clase. Encuentre la mediana del peso de los estudiantes:
| Peso (en kg): | 40 – 45 | 45 – 50 | 50 – 55 | 55 – 60 | 60 – 65 | 65 – 70 | 70 – 75 |
| No de estudiantes: | 2 | 3 | 8 | 6 | 6 | 3 | 2 |
Solución:
Peso (en kg) Número de estudiantes fi Frecuencia acumulada (cf) 40 – 45 2 2 45-50 3 5 50-55 8 13 55-60 6 19 60-65 6 25 65-70 3 28 70-75 2 30 El valor de cf justo mayor que n/ 2 (es decir, 30/ 2 = 15) es 19, pertenece al intervalo de clase 55 – 60.
Por lo tanto,
Clase mediana = 55 – 60
dónde,
(l) de clase mediana = 55, (f) de clase mediana = 6, (cf) = 13 y (h) = 5
Tenemos,
= 55 + 10/6 = 56,666 que es aproximadamente 56,67 kg.
Pregunta 10. Encuentra las frecuencias que faltan y la mediana para la siguiente distribución si la media es 1.46
| Nº de accidentes: | 0 | 1 | 2 | 3 | 4 | 5 | Total |
| Frecuencias (nº de días): | 46 | ? | ? | 25 | 10 | 5 | 200 |
Solución:
Nº de accidentes (x) Nº de días (f) efectos especiales 0 46 0 1 X X 2 y 2 años 3 25 75 4 10 40 5 5 25 norte = 200 Suma = x + 2y + 140 Ya que, sabemos,
norte = 200
Sustituyendo valores, obtenemos,
⇒ 46 + x + y + 25 + 10 + 5 = 200
⇒ x + y = 200 – 46 – 25 – 10 – 5
⇒ x + y = 114…… (yo)
Además, Media = 1.46
⇒ Suma/ N = 1,46
Sustituyendo valores,
⇒ (x + 2y + 140)/ 200 = 1,46
⇒ x + 2y = 292 – 140
⇒ x + 2y = 152 …….(ii)
Resolviendo de (i) y (ii), obtenemos
x + 2y – x – y = 152 – 114
⇒ y = 38
Y, x = 114 – 38 = 76 (de la ecuación (i))
Ahora, poniendo los valores, obtenemos,
N = 200 N/2 = 200/2 = 100
Entonces, la frecuencia acumulada apenas mayor que N/2 es 122
Y, por lo tanto, la mediana es 1.
Publicación traducida automáticamente
Artículo escrito por mallikagupta90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA