Factoriza cada una de las siguientes expresiones:
Pregunta 13. 8x 2 y 3 -x 5
Solución:
⇒ x 2 ((2y) 3 – x 3 )
⇒ x 2 (2y-x)((2y) 2 +2xy+x 2 ) [x 3 -y 3 =(xy)(x 2 +xy+y 2 )]
⇒ x2 ( 2y -x)( 4y2 + 2xy+ x2 )
Por lo tanto, 8x 3 y 3 -x 5 = x 2 (2y-x)(4y 2 +2xy+x 2 )
Pregunta 14. 1029 – 3x 3
Solución:
⇒ 3 (343 – x 3 )
⇒ 3(7 3 – x 3 ) [x 3 -y 3 =(xy)(x 2 +xy+y 2 )]
⇒ 3 (7-x)(7 2 +7x+x 2 )
Por lo tanto, 1029 – 3x 3 = 3 (7-x)(7 2 +7x+x 2 )
Pregunta 15. x 6 + y 6
Solución:
⇒ (x 2 ) 3 + (y 2 ) 3
⇒ (x 2 +y 2 )((x 2 ) 2 -(xy) 2 +(y 2 ) 2 )
⇒ (x 2 +y 2 )(x 4 -x 2 y 2 +y 4 ) [x 3 +y 3 =(x+y)(x 2 -xy+y 2 )]
Por lo tanto, x 6 +y 6 = (x 2 +y 2 )(x 4 -x 2 y 2 +y 4 )
Pregunta 16. x 3 y 3 +1
Solución:
⇒ (xy) 3 + 1 3
⇒(xy+1)((xy) 2 -xy+1 2 ) [x 3 +y 3 =(x+y)(x 2 -xy+y 2 )]
⇒ (xy+1) (x 2 y 2 – xy +1)
Por lo tanto, x 3 y 3 +1 = (xy+1) (x 2 y 2 – xy +1)
Pregunta 17. x 4 y 4 – xy
Solución:
⇒ xy(x 3 y 3 – 1)
⇒ xy ((xy) 3 – 1 3 ) [x 3 -y 3 =(xy)(x 2 +xy+y 2 )]
⇒ xy (xy -1)((xy) 2 +xy +1 2 )
⇒ xy (xy-1)(x 2 y 2 + xy+1)
Por lo tanto, x 4 y 4 – xy = xy (xy-1)(x 2 y 2 + xy+1)
Pregunta 18. a 12 +b 12
Solución:
⇒ (a 4 ) 3 +(b 4 ) 3
⇒ (a 4 +b 4 )((a 4 ) 2 -a 4 b 4 +(b 4 ) 2 ) [x 3 +y 3 =(x+y)(x 2 -xy+y 2 )]
⇒ (a 4 +b 4 )(a 8 -a 4 b 4 +b 8 )
Por lo tanto, a 12 +b 12 = (a 4 +b 4 )(a 8 -a 4 b 4 +b 8 )
Pregunta 19. x 3 +6x 2 +12x+16
Solución:
⇒x3 + 6×2 + 12x+8+8
⇒ x3 +3*x2 * 2 + 3 *x*2 2 +2 3 +8 [a 3 +3a 2 b+3ab 2 +b 3 = (a+b) 3 ]
⇒ (x+2) 3 +2 3
⇒ (x+2+2)((x+2) 2 -2(x+2)+2 2 ) [x 3 +y 3 =(x+y)(x 2 -xy+y 2 )]
⇒ (x+4)(x 2 +2 2 +4x-2x-4+4)
⇒(x+4)(x 2 +4+2x) [(a+b) 2 =a 2 +b 2 +2ab]
Por lo tanto, x 3 +6x 2 +12x+16 = (x+4)(x 2 +4+2x)
Pregunta 20. a 3 +b 3 +a+b
Solución:
⇒ (a 3 +b 3 )+1(a+b)
⇒ (a+b)(a 2 -ab+b 2 )+1(a+b) [a 3 +b 3 = (a+b)(a 2 -ab+b 2 )]
⇒ (a+b)(a 2 -ab +b 2 +1)
Por lo tanto, a 3 +b 3 +a+b = (a+b)(a 2 -ab +b 2 +1)
Pregunta 21. 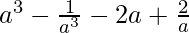
Solución:
⇒
⇒
⇒
⇒
⇒
Por lo tanto,
Pregunta 22. 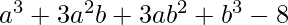
Solución:
⇒ (a+b) 3 -8 [a 3 +3a 2 b+3ab 2 +b 3 = (a+b) 3 ]
⇒ (a+b) 3 – 2 3
⇒ (a+b-2) ((a+b) 2 +2(a+b)+2 2 )
⇒(a+b-2)(a 2 +2ab+b 2 +2a+2b+4)
Por lo tanto, a 3 +3a 2 b+3ab 2 +b 3 -8 = (a+b-2)(a 2 +2ab+b 2 +2a+2b+4)
Pregunta 23. 8a 3 – b 3 -4ax+2bx
Solución:
⇒ (2a) 3 – b 3 -2x(2a -b)
⇒ (2a-b)((2a) 2 +2ab + b 2 ) -2x(2a-b) [x 3 -y 3 =(xy)(x 2 +xy+y 2 )]
⇒ (2a-b)(4a 2 +2ab + b 2 -2x)
Por lo tanto, 8a 3 -b 3 -4ax+2bx = (2a-b)(4a 2 +2ab + b 2 -2x)
Pregunta 24.
(i) 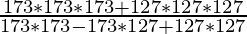
Solución:
⇒
⇒ \frac{(173+127)(173^2-173*127+127^2)}{173^2-173*127+127^2} [a 3 +b 3 =(a+b)(a 2 +b 2 -ab)]
⇒ 173+127
⇒ 300
(ii) 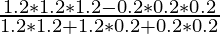
Solución:
⇒ \frac{1.2^3-0.2^3}{1.2^2+1.2*0.2+0.2^2} [a 3 -b 3 =(ab)(a 2 +b 2 +ab)]
⇒
⇒ 1,2 – 0,2
⇒ 1.0
(iii) 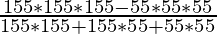
Solución:
⇒ \frac{153^3-55^3}{155^2+155*55+55^2} [a 3 -b 3 =(ab)(a 2 +b 2 +ab)]
⇒
⇒ 155-55
⇒ 100
Publicación traducida automáticamente
Artículo escrito por ranshu1601 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA